Article contents
Monotone reducibility and the family of infinite sets
Published online by Cambridge University Press: 12 March 2014
Abstract
Let A and B be subsets of the space 2N of sets of natural numbers. A is said to be Wadge reducible to B if there is a continuous map Φ from 2N into 2N such that A = Φ−1 (B); A is said to be monotone reducible to B if in addition the map Φ is monotone, that is, a ⊂ b implies Φ(a) ⊂ Φ(b). The set A is said to be monotone if a ∈ A and a ⊂ b imply b ∈ A. For monotone sets, it is shown that, as for Wadge reducibility, sets low in the arithmetical hierarchy are nicely ordered. The 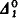 sets are all reducible to the (
sets are all reducible to the (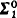 but not
but not 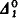 ) sets, which are in turn all reducible to the strictly
) sets, which are in turn all reducible to the strictly 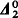 sets, which are all in turn reducible to the strictly
sets, which are all in turn reducible to the strictly 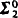 sets. In addition, the nontrivial
sets. In addition, the nontrivial 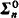 sets all have the same degree for n ≤ 2. For Wadge reducibility, these results extend throughout the Borel hierarchy. In contrast, we give two natural strictly
sets all have the same degree for n ≤ 2. For Wadge reducibility, these results extend throughout the Borel hierarchy. In contrast, we give two natural strictly 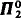 monotone sets which have different monotone degrees. We show that every
monotone sets which have different monotone degrees. We show that every 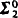 monotone set is actually
monotone set is actually 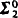 positive. We also consider reducibility for subsets of the space of compact subsets of 2N. This leads to the result that the finitely iterated Cantor-Bendixson derivative Dn is a Borel map of class exactly 2n, which answers a question of Kuratowski.
positive. We also consider reducibility for subsets of the space of compact subsets of 2N. This leads to the result that the finitely iterated Cantor-Bendixson derivative Dn is a Borel map of class exactly 2n, which answers a question of Kuratowski.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 3
- Cited by

