Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T12:26:29.487Z Has data issue: false hasContentIssue false
  • English
  • Français

More on imaginaries in p-adic fields

Published online by Cambridge University Press:  12 March 2014

Philip Scowcroft
Philip Scowcroft*
Affiliation:
Department of Mathematics, Wesleyan University, Middletown, CT 06459, USA, E-mail: pscowcroft@wesleyan.edu
Get access Rights & Permissions [Opens in a new window]

Extract

According to [4, p. 1154], a complete L-theory T eliminates imaginaries just in case for every L-formula φ(x1,… , xm, y1, …, yn), every model M of T, and every ā Є Mn, there is a subset A of M's domain with the following property: if N ≽ M and f is an automorphism of N, then

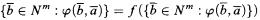
if and only if

Among the several equivalent conditions discussed in [4, p. 1155], one may single out the following: if T is a complete theory in which two distinct objects are definable, T eliminates imaginaries just in case every T-definable n-ary equivalence relation may be defined by a formula

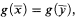
where g is a T-definable n-ary function taking k-tuples as values (for some natural number k).

Say that an L-structure M eliminates imaginaries just in case Th(M) does. If L is the language of rings with unit, [4, p. 1158] shows that any algebraically closed field eliminates imaginaries, and [2, p. 629] points out that any real-closed field eliminates imaginaries.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 1 , March 1997 , pp. 1 - 13
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bélair, L., Substructures and uniform elimination for p-adic fields, Annals of Pure and Applied Logic, vol. 39 (1988), pp. 1–17.CrossRefGoogle Scholar
[2]van den Dries, L., Algebraic theories with definable Skolemfunctions, this Journal, vol. 49 (1984), pp. 625–629.Google Scholar
[3]Makkai, M., A survey of basic stability theory, with particular emphasis on orthogonality and regular types, Israel Journal of Mathematics, vol. 49 (1984), pp. 181–238.CrossRefGoogle Scholar
[4]Poizat, B., Une théorie de Galois imaginaire, this Journal, vol. 48 (1983), pp. 1151–1170.Google Scholar
[5]Scowcroft, P. and van den Dries, L., On the structure of semialgebraic sets over p-adic fields, this Journal, vol. 53 (1988), pp. 1138–1164.Google Scholar
[6]Scowcroft, P. and Macintyre, A., On the elimination of imaginaries from certain valued fields, Annals of Pure and Applied Logic, vol. 61 (1993), pp. 241–276.CrossRefGoogle Scholar