No CrossRef data available.
Article contents
MORE ON YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
Published online by Cambridge University Press: 27 January 2025
Abstract
This is a continuation of the paper [J. Symb. Log. 87 (2022), 1065–1092]. For an ideal  $\mathcal {I}$ on
$\mathcal {I}$ on 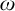 $\omega $ we denote
$\omega $ we denote  $\mathcal {D}_{\mathcal {I}}=\{f\in \omega ^{\omega }: f^{-1}[\{n\}]\in \mathcal {I} \text { for every } n\in \omega \}$ and write
$\mathcal {D}_{\mathcal {I}}=\{f\in \omega ^{\omega }: f^{-1}[\{n\}]\in \mathcal {I} \text { for every } n\in \omega \}$ and write 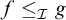 $f\leq _{\mathcal {I}} g$ if
$f\leq _{\mathcal {I}} g$ if 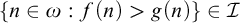 $\{n\in \omega :f(n)>g(n)\}\in \mathcal {I}$, where
$\{n\in \omega :f(n)>g(n)\}\in \mathcal {I}$, where 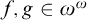 $f,g\in \omega ^{\omega }$.
$f,g\in \omega ^{\omega }$.
We study the cardinal numbers 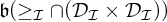 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$ describing the smallest sizes of subsets of
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$ describing the smallest sizes of subsets of 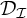 $\mathcal {D}_{\mathcal {I}}$ that are unbounded from below with respect to
$\mathcal {D}_{\mathcal {I}}$ that are unbounded from below with respect to 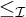 $\leq _{\mathcal {I}}$.
$\leq _{\mathcal {I}}$.
In particular, we examine the relationships of 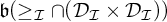 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$ with the dominating number
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$ with the dominating number 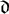 $\mathfrak {d}$. We show that, consistently,
$\mathfrak {d}$. We show that, consistently, 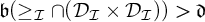 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))>\mathfrak {d}$ for some ideal
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))>\mathfrak {d}$ for some ideal 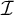 $\mathcal {I}$, however
$\mathcal {I}$, however 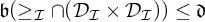 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))\leq \mathfrak {d}$ for all analytic ideals
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))\leq \mathfrak {d}$ for all analytic ideals 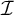 $\mathcal {I}$. Moreover, we give example of a Borel ideal with
$\mathcal {I}$. Moreover, we give example of a Borel ideal with 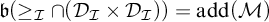 $\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))=\operatorname {\mathrm {add}}(\mathcal {M})$.
$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))=\operatorname {\mathrm {add}}(\mathcal {M})$.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


