Article contents
Nonisomorphism of lattices of recursively enumerable sets
Published online by Cambridge University Press: 12 March 2014
Extract
Let ω be the set of natural numbers, let 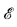 be the lattice of recursively enumerable subsets of ω, and let
be the lattice of recursively enumerable subsets of ω, and let 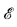 A be the lattice of subsets of ω which are recursively enumerable in A. If U, V ⊆ ω, put U =* V if the symmetric difference of U and V is finite.
A be the lattice of subsets of ω which are recursively enumerable in A. If U, V ⊆ ω, put U =* V if the symmetric difference of U and V is finite.
A natural and interesting question is then to discover what the relation is between the Turing degree of A and the isomorphism class of 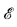 A. The first result of this form was by Lachlan, who proved [6] that there is a set A ⊆ ω such that
A. The first result of this form was by Lachlan, who proved [6] that there is a set A ⊆ ω such that 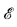 A ≇
A ≇ 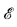 . He did this by finding a set A ⊆ ω and a set C ϵ
. He did this by finding a set A ⊆ ω and a set C ϵ 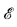 A such that the structure ({W ϵ
A such that the structure ({W ϵ 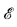 A∣W ⊇ C},∪,∩)/=* is a Boolean algebra and is not isomorphic to the structure ({W ϵ
A∣W ⊇ C},∪,∩)/=* is a Boolean algebra and is not isomorphic to the structure ({W ϵ 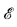 ∣W ⊇ D},∪,∩)/=* for any D ϵ
∣W ⊇ D},∪,∩)/=* for any D ϵ 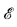 . There is a nonrecursive ordinal which is recursive in the set A which he constructs, so his set A is not
. There is a nonrecursive ordinal which is recursive in the set A which he constructs, so his set A is not 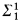 (see, for example, Shoenfield [11] for a definition of what it means for a set A ⊆ ω to be
(see, for example, Shoenfield [11] for a definition of what it means for a set A ⊆ ω to be 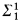 ). Feiner then improved this result substantially by proving [1] that for any B ⊆ ω,
). Feiner then improved this result substantially by proving [1] that for any B ⊆ ω, 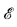 B′ ≇
B′ ≇ 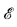 B, where B′ is the Turing jump of B. To do this, he showed that for each X ⊆= ω there is a Boolean algebra which is
B, where B′ is the Turing jump of B. To do this, he showed that for each X ⊆= ω there is a Boolean algebra which is 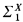 but not
but not 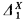 and then applied a theorem of Lachlan [6] (definitions of
and then applied a theorem of Lachlan [6] (definitions of 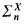 and
and 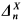 Boolean algebras will be given in §2). Feiner's result is of particular interest for the case B = ⊘, for it shows that the set A of Lachlan can actually be chosen to be arithmetical (in fact, ⊘′), answering a question that Lachlan posed in his paper. Little else has been known.
Boolean algebras will be given in §2). Feiner's result is of particular interest for the case B = ⊘, for it shows that the set A of Lachlan can actually be chosen to be arithmetical (in fact, ⊘′), answering a question that Lachlan posed in his paper. Little else has been known.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 2
- Cited by

