Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-10T22:02:08.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonstandard characterizations of recursive saturation and resplendency

Published online by Cambridge University Press:  12 March 2014

Stuart T. Smith
Stuart T. Smith*
Affiliation:
Department of Mathematics and Statistics, Simon Fraser University, Burnaby, British Columbia V5A 1S6, Canada Department of Mathematics and Computer Science, Ben-Gurion University of the Negev, Beersheva, Israel
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove results about nonstandard formulas in models of Peano arithmetic which complement those of Kotlarski, Krajewski, and Lachlan in [KKL] and [L]. This enables us to characterize both recursive saturation and resplendency in terms of statements about nonstandard sentences. Specifically, a model 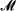of PA is recursively saturated iff 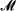is nonstandard and 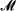-logic is consistent. 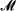is resplendent iff 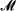is nonstandard, 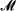-logic is consistent, and every sentence φ which is consistent in 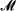-logic is contained in a full satisfaction class for 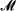. Thus, for models of PA, recursive saturation can be expressed by a (standard) 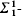-sentence and resplendency by a 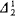-sentence.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 3 , September 1987 , pp. 842 - 863
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The author acknowledges support of NSERC grant no. 5403.

References

REFERENCES

[BS] Barwise, J. and Schlipf, J., An introduction to recursively saturated and resplendent models, this Journal, vol. 41 (1976), pp. 531–536.Google Scholar
[Ka] Kaufmann, M., A rather classless model, Proceedings of the American Mathematical Society, vol. 62 (1977), pp. 330–333.CrossRefGoogle Scholar
[K1] Kleene, S. C., Finite axiomatizability of theories in the predicate calculus using additional predicate symbols, Two papers on the predicate calculus, Memoirs of the American Mathematical Society, no. 10, American Mathematical Society, Providence, Rhode Island, 1952, pp. 27–68.Google Scholar
[KKL] Kotlarski, H., Krajewski, S., and Lachlan, A., Construction of satisfaction classes for nonstandard models, Canadian Mathematical Bulletin, vol. 24 (1981), pp. 283–293.CrossRefGoogle Scholar
[L] Lachlan, A., Full satisfaction classes and recursive saturation, Canadian Mathematical Bulletin, vol. 24 (1981), pp. 295–297.CrossRefGoogle Scholar
[Sm1] Smith, S., Nonstandard syntax and semantics and full satisfaction classes for models of arithmetic, Ph.D. Thesis, Yale University, New Haven, Connecticut, 1984.Google Scholar
[Sm2] Smith, S., Nonstandard definability, Annals of Pure and Applied Logic (to appear).Google Scholar