Article contents
Note on the Kondo-Addison theorem
Published online by Cambridge University Press: 12 March 2014
Extract
The Kondo-Addison theorem says that every 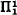 set A of reals contains a real which is implicit
set A of reals contains a real which is implicit 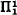 (for short, Imp). Any real which is Imp is constructible, and it is the main purpose of this note to show that a close examination of the usual Kondo-Addison argument allows us to compute (in terms of the ordinals associated with A by the classical representation theorem) where in the constructible hierarchy an element of A ∩ Imp must occur. This result is related to a basis theorem of Barwise and Fisher [1] and is accompanied by a strong counterexample which shows that certain tepid improvements of their theorem (and, a fortiori, of the main theorem in this note) are impossible. As a final flourish, the ‘classifying ordinals’ used to compute the locations of the singletons are themselves characterized using an idea from [1].
(for short, Imp). Any real which is Imp is constructible, and it is the main purpose of this note to show that a close examination of the usual Kondo-Addison argument allows us to compute (in terms of the ordinals associated with A by the classical representation theorem) where in the constructible hierarchy an element of A ∩ Imp must occur. This result is related to a basis theorem of Barwise and Fisher [1] and is accompanied by a strong counterexample which shows that certain tepid improvements of their theorem (and, a fortiori, of the main theorem in this note) are impossible. As a final flourish, the ‘classifying ordinals’ used to compute the locations of the singletons are themselves characterized using an idea from [1].
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 1
- Cited by

