Article contents
The number of proofs for a BCK-formula
Published online by Cambridge University Press: 12 March 2014
Extract
In this note, we give a necessary and sufficient condition for a BCK-formula to have the unique normal form proof.
We call implicational propositional formulas formulas for short. BCK-formulas are the formulas which are derivable from axioms B = (a → b) → (c → a) → c → b, C = (a→b→c)→b→a→c, and K = a→b→a by substitution and modus ponens. It is known that the property of being a BCK-formula is decidable (Jaskowski [11, Theorem 6.5], Ben-Yelles [3, Chapter 3, Theorem 3.22], Komori [12, Corollary 6]). The set of BCK-formulas is identical to the set of provable formulas in the natural deduction system with the following two inference rules.
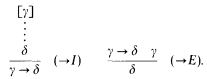
Here γ occurs at most once in (→I). By the formulae-as-types correspondence [10], this set is identical to the set of type-schemes of closed BCK-λ-terms. (See [5].) A BCK-λ-term is a λ-term in which no variable occurs twice. Basic notion concerning the type assignment system can be found [4]. Uniqueness of normal form proofs has been known for balanced formulas. (See [2,14].) It is related to the coherence theorem in cartesian closed categories. A formula is balanced when no variable occurs more than twice in it. It was shown in [8] that the proofs of balanced formulas are BCK-proofs. Relevantly balanced formulas were defined in [9], and it was proved that such formulas have unique normal form proofs. Balanced formulas are included in the set of relevantly balanced formulas.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 3
- Cited by

