Article contents
On a conjecture of Dobrinen and Simpson concerning almost everywhere domination
Published online by Cambridge University Press: 12 March 2014
Extract
Dobrinen and Simpson [4] introduced the notions of almost everywhere domination and uniform almost everywhere domination to study recursion theoretic analogues of results in set theory concerning domination in generic extensions of transitive models of ZFC and to study regularity properties of the Lebesgue measure on 2ω in reverse mathematics. In this article, we examine one of their conjectures concerning these notions.
Throughout this article, ≤T denotes Turing reducibility and μ denotes the Lebesgue (or “fair coin”) probability measure on 2ω given by
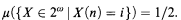
A property holds almost everywhere or for almost all X ∈ 2ω if it holds on a set of measure 1. For f, g ∈ ωω, f dominatesg if ∃m∀n < m(f(n) > g(n)).
(Dobrinen, Simpson). A set A ∈ 2ωis almost everywhere (a.e.) dominating if for almost all X ∈ 2ω and all functions g ≤TX, there is a function f ≤TA such that f dominates g. A is uniformly almost everywhere (u.a.e.) dominating if there is a function f ≤TA such that for almost all X ∈ 2ω and all functions g ≤TX, f dominates g.
There are several trivial but useful observations to make about these definitions. First, although these properties are stated for sets, they are also properties of Turing degrees. That is, a set is (u.)a.e. dominating if and only if every other set of the same degree is (u.)a.e. dominating. Second, both properties are closed upwards in the Turing degrees. Third, u.a.e. domination implies a.e. domination. Finally, if A is u.a.e. dominating, then there is a function f ≤TA which dominates every computable function.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2006
References
REFERENCES
- 14
- Cited by

