Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T10:40:09.716Z Has data issue: false hasContentIssue false
  • English
  • Français

ON EXTENSIONS OF PARTIAL ISOMORPHISMS

Part of: Structure and classification of infinite or finite groups Model theory

Published online by Cambridge University Press:  20 July 2020

MAHMOOD ETEDADIALIABADI  and
SU GAO
MAHMOOD ETEDADIALIABADI
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NORTH TEXAS 1155 UNION CIRCLE #311430, DENTON, TX76203, USAE-mail: mahmood.etedadialiabadi@unt.eduE-mail: sgao@unt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study a notion of HL-extension (HL standing for Herwig–Lascar) for a structure in a finite relational language $\mathcal {L}$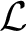 . We give a description of all finite minimal HL-extensions of a given finite $\mathcal {L}$ 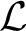-structure. In addition, we study a group-theoretic property considered by Herwig–Lascar and show that it is closed under taking free products. We also introduce notions of coherent extensions and ultraextensive $\mathcal {L}$ 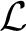-structures and show that every countable $\mathcal {L}$ 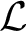-structure can be extended to a countable ultraextensive structure. Finally, it follows from our results that the automorphism group of any countable ultraextensive $\mathcal {L}$ 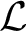-structure has a dense locally finite subgroup.

Keywords

Hrushovski propertyextension property for partial automorphisms (EPPA)partial isomorphismHL-extensionHL-mapcoherentultraextensiveultrahomogeneouslocally finiteHenson graph

MSC classification

Primary: 03C13: Finite structures 03C55: Set-theoretic model theory
Secondary: 20E06: Free products, free products with amalgamation, Higman-Neumann-Neumann extensions, and generalizations 20E26: Residual properties and generalizations; residually finite groups
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 1 , March 2022 , pp. 416 - 435
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Coulbois, T., Free product, profinite topology and finitely generated subgroups . International Journal of Algebra and Computation , vol. 11 (2001), no. 2, pp. 171–184.CrossRefGoogle Scholar
Etedadialiabadi, M. and Gao, S., On extensions of partial isometries. Preprint, 2019, arXiv:1903.09723.Google Scholar
Herwig, B. and Lascar, D., Extending partial automorphisms and the profinite topology on free groups . Transactions of the American Mathematical Society , vol. 352 (2000), no.5, 1985–2021.CrossRefGoogle Scholar
Hrushovski, E., Extending partial isomorphisms of graphs . Combinatorica , vol. 12 (1992), no. 4, pp. 411–416.10.1007/BF01305233CrossRefGoogle Scholar
Hubička, J., Konečnỳ, M., and Nešetřil, J., A combinatorial proof of the extension property for partial isometries . Commentationes Mathematicae Universitatis Carolinae , vol. 60 (2019), no. 1, pp. 39–47.Google Scholar
Ribes, L. and Zalesskii, P. A., On the profinite topology on a free group . Bulletin of the London Mathematical Society , vol. 25 (1993), no. 1, pp. 37–43.CrossRefGoogle Scholar
Rosendal, C., Finitely approximable groups and actions Part I: The Ribes–Zalesskii property , this Journal, vol. 76 (2011), no. 4, pp. 1297–1306.Google Scholar
Siniora, D. and Solecki, S., Coherent extension of partial automorphisms, free amalgamation and automorphism groups, this Journal, vol. 85 (2020), no. 1, pp. 199–223.Google Scholar
Solecki, S., Extending partial isometries . Israel Journal of Mathematics , vol. 150 (2005), pp. 315–331.CrossRefGoogle Scholar