Article contents
On the inconsistency of systems similar to 
Published online by Cambridge University Press: 12 March 2014
Extract
This note shows that the inconsistency proof of the system  of illative combinatory logic given in [1] can be simplified as well as extended to the absolute inconsistency of a more general system.
of illative combinatory logic given in [1] can be simplified as well as extended to the absolute inconsistency of a more general system.
One extension of the result in [1] lies in the fact that the following weakened form of the deduction theorem for implication will lead to the inconsistency:
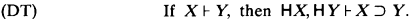
Also the inconsistency follows almost as easily for

as it does for ⊢ H2X for arbitrary X, so we will consider the more general case.
The only properties we require other than (DT), (1) and Rule Eq for equality are modus ponens,
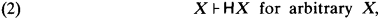
and

Let G = [x] Hn−1x⊃: . … H2x⊃ :Hx⊃ . x ⊃ A, where A is arbitrary. Then if Y is the paradoxical combinator and X = YG, X = GX.
Now X ⊂ X, i.e.,
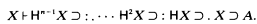
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
References
REFERENCE
- 3
- Cited by

