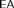Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Walsh, James
2023.
Evitable iterates of the consistency operator.
Computability,
Vol. 12,
Issue. 1,
p.
59.
Steel, John R.
2024.
The Philosophy of Penelope Maddy.
Vol. 31,
Issue. ,
p.
13.
Hamkins, Joel David
2025.
Nonlinearity and illfoundedness in the hierarchy of large cardinal consistency strength.
Monatshefte für Mathematik,