Article contents
On the representation of Herbrand functions in algebraically closed fields
Published online by Cambridge University Press: 12 March 2014
Extract
1. Let X be a statement which is formulated in the lower predicate calculus in terms of the relations of addition, multiplication, and equality, and — possibly — of the elements of a given commutative field M. Suppose moreover that X is in prenex normal form, e.g.
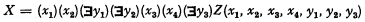
where Z does not include any further quantifiers. In order that X be satisfied by the algebraic closure M* of M, it is necessary and sufficient that there exist Herbrand functions (or choice functions) φ1(x1, x2), φ2(x1, x2), φ3(x1, x2, x3, x4) with arguments ranging over M* and taking values in M* such that
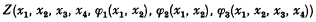
holds for all x1, x2, x3, x4 in M*. In general the definition of these functions is far from being unique, and a priori they bear no relation to the functions which are defined ‘naturally’ in M* i.e. the rational, and more generally the algebraic, functions with coefficients in M or M*. However, we shall show in the present paper that the entire domain of variation of the arguments x1, x2, x3, x4 — regarded as the affine space S4 over M* — can be divided up into a finite number of regions Di such that in each Di the functions ϕk can be chosen as algebraic functions of their arguments. Indeed, our complete result (§ 3) proves rather more than that. In particular, it turns out that the regions Di may be taken as differences of algebraic varieties in M*.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1957
References
REFERENCES
- 2
- Cited by

