Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-30T00:41:21.009Z Has data issue: false hasContentIssue false
  • English
  • Français

ON WIDE ARONSZAJN TREES IN THE PRESENCE OF MA

Part of: Set theory

Published online by Cambridge University Press:  07 September 2020

MIRNA DŽAMONJA  and
SAHARON SHELAH
MIRNA DŽAMONJA
Affiliation:
INSTITUT D'HISTOIRE ET DE PHILOSOPHIE DES SCIENCES ET DES TECHNIQUES (IHPST) CNRS & UNIVERSITÉ PANTHÉON-SORBONNE 13 RUE DE FOUR, 75006 PARIS, FRANCE INSTITUTE OF MATHEMATICS CZECH ACADEMY OF SCIENCES ITNÁ 25, 115 76 PRAGUE, CZECH REPUBLIC E-mail: M.Dzamonja@uea.ac.uk URL: mirna.dzamonja@univ-paris1.fr
SAHARON SHELAH
Affiliation:
DEPARTMENT OF MATHEMATICS HEBREW UNIVERSITY OF JERUSALEM 91904, GIVAT RAM, ISRAEL E-mail:shelah@math.huji.ac.il URL: http://shelah.logic.at
Get access Rights & Permissions [Opens in a new window]

Abstract

A wide Aronszajn tree is a tree of size and height 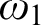$\omega _{1}$ with no uncountable branches. We prove that under 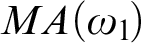$MA(\omega _{1}\!)$ there is no wide Aronszajn tree which is universal under weak embeddings. This solves an open question of Mekler and Väänänen from 1994.

We also prove that under 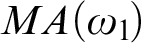$MA(\omega _{1}\!)$, every wide Aronszajn tree weakly embeds in an Aronszajn tree, which combined with a result of Todorčević from 2007, gives that under 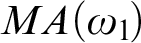$MA(\omega _{1}\!)$ every wide Aronszajn tree embeds into a Lipschitz tree or a coherent tree. We also prove that under 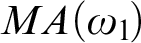$MA(\omega _{1}\!)$ there is no wide Aronszajn tree which weakly embeds all Aronszajn trees, improving the result in the first paragraph as well as a result of Todorčević from 2007 who proved that under 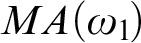$MA(\omega _{1}\!)$ there are no universal Aronszajn trees.

Keywords

wide Aronszajn treeMartin axiomuniversality

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E35: Consistency and independence results 03E50: Continuum hypothesis and Martin's axiom

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 1 , March 2021 , pp. 210 - 223
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Baumgartner, J. E., Malitz, J., and Reinhardt, W., Embedding trees in the rationals . Proceedings of the National Academy of Sciences United States of America , vol. 67 (1970), no. 4, pp. 1748–1753.CrossRefGoogle ScholarPubMed
Džamonja, M. and Väänänen, J., A family of trees with no uncountable branches . Topology Proceedings , vol. 28 (2004), no. 1, pp. 113–132. Spring Topology and Dynamical Systems Conference.Google Scholar
Džamonja, M. and Väänänen, J., Chain models, trees of singular cardinality and dynamic EF-games . Journal of Mathematical Logic , vol. 11 (2011), no. 1, pp. 61–85.CrossRefGoogle Scholar
Jech, T., Set Theory , third millenium ed., Springer-Verlag, Berlin, 2003.Google Scholar
Kurepa, Ð., Transformations monotones des ensembles partiallement ordonnes , Comptes Rendus Mathématique , vol. 205 , Académie de Sciences, Paris, 1937, pp. 1033–1035.Google Scholar
Kurepa, Ð., Transformations monotones des ensembles partiallement ordonnes , Selected Papers of Ðuro Kurepa (Ivic, A., Mamuzic, Z., Mijajlovic, Z., and Todorcevic, S., editors), Matematički Institut u Beogradu, Belgrade, 1996, pp. 165–186.Google Scholar
Mekler, A. and Väänänen, J., Trees and ${\varPi}_1^1$ -subsets of ${\vphantom{0}}^{\omega_1}\omega_1$ , this Journal, vol. 58 (1993), no. 3, pp. 1052–1070.Google Scholar
Moore, J. T., Structural analysis of Aronszajn trees , Logic Colloquium 2005 (Dimitracopoulos, C., Newelski, L., Normann, D. and Steel, J., editors), Lecture Notes in Logic, vol. 28, Cambridge University Press, Cambridge, 2006, pp. 85–107.Google Scholar
Sikorski, R., Remarks on some topological spaces of high power . Fundamenta Mathematicae , vol. 37 (1949), pp. 125–136.CrossRefGoogle Scholar
Todorčević, S., Lipschitz maps on trees . Journal of the Institute of Mathematics of Jussieu , vol. 6 (2007), no. 3, pp. 527–556.CrossRefGoogle Scholar
Todorčević, S., Walks on Ordinals and their Characteristics , Progress in Mathematics, vol. 263, Birkhäuser Verlag, Basel, 2007.CrossRefGoogle Scholar
Todorčević, S., Trees and linearly ordered sets , Handbook of Set-Theoretic Topology (Kunen, K. and Vaughan, J. E., editors), North Holland, Amsterdam, 1984, pp. 235–293.CrossRefGoogle Scholar