Hostname: page-component-7dd5485656-c8zdz Total loading time: 0 Render date: 2025-10-29T16:34:35.434Z Has data issue: false hasContentIssue false
  • English
  • Français

PA RELATIVE TO AN ENUMERATION ORACLE

Part of: Computability and recursion theory

Published online by Cambridge University Press:  18 July 2022

JUN LE GOH ,
ISKANDER SH. KALIMULLIN ,
JOSEPH S. MILLER  and
MARIYA I. SOSKOVA
JUN LE GOH
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN–MADISON 480 LINCOLN DRIVE, MADISON, WI 53706, USA E-mail: junle.goh@wisc.edu E-mail: jmiller@math.wisc.edu
ISKANDER SH. KALIMULLIN
Affiliation:
N.I. LOBACHEVSKY INSTITUTE OF MATHEMATICS AND MECHANICS KAZAN FEDERAL UNIVERSITY KAZAN, RUSSIA E-mail: Iskander.Kalimullin@kpfu.ru
JOSEPH S. MILLER
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN–MADISON 480 LINCOLN DRIVE, MADISON, WI 53706, USA E-mail: junle.goh@wisc.edu E-mail: jmiller@math.wisc.edu
MARIYA I. SOSKOVA*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN–MADISON 480 LINCOLN DRIVE, MADISON, WI 53706, USA E-mail: junle.goh@wisc.edu E-mail: jmiller@math.wisc.edu
*
E-mail: msoskova@math.wisc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Recall that B is PA relative to A if B computes a member of every nonempty 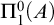$\Pi ^0_1(A)$ class. This two-place relation is invariant under Turing equivalence and so can be thought of as a binary relation on Turing degrees. Miller and Soskova [23] introduced the notion of a 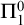$\Pi ^0_1$ class relative to an enumeration oracle A, which they called a 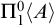$\Pi ^0_1{\left \langle {A}\right \rangle }$ class. We study the induced extension of the relation B is PA relative to A to enumeration oracles and hence enumeration degrees. We isolate several classes of enumeration degrees based on their behavior with respect to this relation: the PA bounded degrees, the degrees that have a universal class, the low for PA degrees, and the 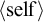${\left \langle {\text {self}\kern1pt}\right \rangle }$-PA degrees. We study the relationship between these classes and other known classes of enumeration degrees. We also investigate a group of classes of enumeration degrees that were introduced by Kalimullin and Puzarenko [14] based on properties that are commonly studied in descriptive set theory. As part of this investigation, we give characterizations of three of their classes in terms of a special sub-collection of relativized 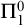$\Pi ^0_1$ classes—the separating classes. These three can then be seen to be direct analogues of three of our classes. We completely determine the relative position of all classes in question.

Keywords

enumeration degreesPA relative toseparating classes

MSC classification

Primary: 03D30: Other degrees and reducibilities
Secondary: 03D32: Algorithmic randomness and dimension

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 4 , December 2023 , pp. 1497 - 1525
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrews, U., Ganchev, H. A., Kuyper, R., Lempp, S., Miller, J. S., Soskova, A. A., and Soskova, M. I., On cototality and the skip operator in the enumeration degrees . Transactions of the American Mathematical Society , vol. 372 (2019), no. 3, pp. 1631–1670.Google Scholar
Andrews, U., Igusa, G., Miller, J. S., and Soskova, M. I., Characterizing the continuous degrees . Israel Journal of Mathematics , vol. 234 (2019), no. 2, pp. 743–767.Google Scholar
Badillo, L. and Harris, C. M., An application of 1-genericity in the ${\varPi}_2^0$ enumeration degrees, Theory and Applications of Models of Computation (Agrawal, M., Cooper, S. B., and Li, A., editors), Lecture Notes in Computer Science, vol. 7287, Springer, Heidelberg, 2012, pp. 604–620.Google Scholar
Badillo, L., Harris, C. M., and Soskova, M. I., Enumeration 1-genericity in the local enumeration degrees . Notre Dame Journal of Formal Logic , vol. 59 (2018), no. 4, pp. 461–489.Google Scholar
Barmpalias, G., Brodhead, P., Cenzer, D., Dashti, S., and Weber, R., Algorithmic randomness of closed sets . Journal of Logic and Computation , vol. 17 (2007), no. 6, pp. 1041–1062.Google Scholar
Cai, M., Ganchev, H. A., Lempp, S., Miller, J. S., and Soskova, M. I., Defining totality in the enumeration degrees . Journal of the American Mathematical Society , vol. 29 (2016), no. 4, pp. 1051–1067.Google Scholar
Cooper, S. B., Partial degrees and the density problem. II. The enumeration degrees of the ${\varSigma}_2$ sets are dense, Journal of Symbolic Logic, vol. 49 (1984), no. 2, pp. 503–513.Google Scholar
Diamondstone, D. and Kjos-Hanssen, B., Martin-Löf randomness and Galton–Watson processes . Annals of Pure and Applied Logic , vol. 163 (2012), no. 5, pp. 519–529.Google Scholar
Downey, R., Hirschfeldt, D. R., Miller, J. S., and Nies, A., Relativizing Chaitin’s halting probability . Journal of Mathematical Logic , vol. 5 (2005), no. 2, pp. 167–192.Google Scholar
Friedberg, R. M. and Rogers, H., Jr., Reducibility and completeness for sets of integers. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 5 (1959), pp. 117–125.Google Scholar
Ganchev, H. A., Kalimullin, I. S., Miller, J. S., and Soskova, M. I., A structural dichotomy in the enumeration degrees, Journal of Symbolic Logic, vol. 87 (2022), pp. 527–544.Google Scholar
Jeandel, E., Enumeration in closure spaces with applications to algebra, preprint, 2017, arXiv:1505.07578.Google Scholar
Jockusch, C. G. Jr. and Soare, R. I., ${\varPi}_1^0$ classes and degrees of theories . Transactions of the American Mathematical Society , vol. 173 (1972), pp. 33–56.Google Scholar
Kalimullin, I. S., Definability of the jump operator in the enumeration degrees . Journal of Mathematical Logic , vol. 3 (2003), no. 2, pp. 257–267.Google Scholar
Kalimullin, I. S. and Puzarenko, V. G., Computability principles on admissible sets . Matematicheskie Trudy , vol. 7 (2004), no. 2, pp. 35–71.Google Scholar
Kihara, T., Ng, K. M., and Pauly, A., Enumeration degrees and non-metrizable topology, preprint, 2020, arXiv:1904.04107. Google Scholar
Kreisel, G., A variant to Hilbert’s theory of the foundations of arithmetic . The British Journal for the Philosophy of Science , vol. 4 (1953), pp. 107–129; errata and corrigenda, vol. 4 (1954), p. 357.Google Scholar
Kučera, A., Measure, ${\varPi}_1^0$ -classes and complete extensions of $\mathsf{PA}$ , Recursion Theory Week (Oberwolfach, 1984) (Ebbinghaus, H.-D., Müller, G. H., and Sacks, G. E., editors), Lecture Notes in Mathematics, vol. 1141, Springer, Berlin, 1985, pp. 245–259.Google Scholar
Lagemann, J., Embedding theorems in the reducibility ordering of the partial degrees . Ph.D. thesis, Massachusetts Institute of Technology, 1971.Google Scholar
McCarthy, E., Cototal enumeration degrees and their applications to effective mathematics . Proceedings of the American Mathematical Society , vol. 146 (2018), no. 8, pp. 3541–3552.Google Scholar
Medvedev, Y. T., Degrees of difficulty of the mass problem . Doklady Akademii Nauk SSSR , vol. 104 (1955), pp. 501–504.Google Scholar
Miller, J. S., Degrees of unsolvability of continuous functions, Journal of Symbolic Logic, vol. 69 (2004), no. 2, pp. 555–584.Google Scholar
Miller, J. S. and Soskova, M. I., Density of the cototal enumeration degrees . Annals of Pure and Applied Logic , vol. 169 (2018), no. 5, pp. 450–462.Google Scholar
Miller, J. S. and Soskova, M. I., Randomness relative to an enumeration oracle, unpublished.Google Scholar
Myhill, J., Creative sets . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik , vol. 1 (1955), pp. 97–108.Google Scholar
Reimann, J. and Slaman, T. A., Measures and their random reals . Transactions of the American Mathematical Society , vol. 367 (2015), no. 7, pp. 5081–5097.Google Scholar
Selman, A. L., Arithmetical reducibilities I . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik , vol. 17 (1971), pp. 335–350.Google Scholar
Solon, B. Y., Total and co-total enumeration degrees . Russian Mathematics , vol. 49 (2005), no. 9, pp. 56–64.Google Scholar
Uspensky, V. A., On computable operations . Doklady Akademii Nauk SSSR , vol. 103 (1955), pp. 775–776.Google Scholar