Article contents
Partitioning pairs of countable sets of ordinals
Published online by Cambridge University Press: 12 March 2014
Extract
In [3], Todorčević showed that ω1 ⇸ [ω1]ω12. In this paper we use similar methods to prove an analogous partition theorem for Pω1(λ), for certain uncountable cardinals λ.
Recall that ω1 → [ω1]ω12, means that for every function f: [ω1]2 → ω1 there is a set A ∈ [ω1]ω1 such that f“[A]2 ≠ ω1, and of course ω1 ⇸ [ω1]ω12, is the negation of this statement. For partition relations onPω1(→) it is customary to partition only those pairs of sets in which the first set is a subset of the second. Thus for A ⊆ Pω1(λ) we define
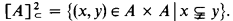
We will write Pω1(λ) → [unbdd]λ2 to mean that for every function f: [Pω1(λ)]⊂2 → λ there is an unbounded set A ⊆ Pω1(λ) such that f“[A]⊂2 ≠ λ, and again Pω1(λ) ⇸ [unbdd]λ2 is the negation of this statement.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
REFERENCES
- 4
- Cited by

