Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ben-Neria, Omer
2015.
The structure of the Mitchell order – II.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 12,
p.
1407.
Ben-Neria, Omer
2016.
The structure of the Mitchell order—I.
Israel Journal of Mathematics,
Vol. 214,
Issue. 2,
p.
945.
Ben-Neria, Omer
and
Müller, Sandra
2021.
Infinite decreasing chains in the Mitchell order.
Archive for Mathematical Logic,
Vol. 60,
Issue. 6,
p.
771.
Apter, Arthur
and
Cummings, James
2023.
Normal measures on large cardinals.
Transactions of the American Mathematical Society, Series B,
Vol. 10,
Issue. 4,
p.
129.

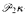 -hypermeasurable and
-hypermeasurable and 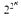 >
> 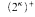 .
.