Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T17:32:02.940Z Has data issue: false hasContentIssue false
  • English
  • Français

PSEUDO-FINITE SETS, PSEUDO-O-MINIMALITY

Part of: Model theory Graph theory Extremal combinatorics

Published online by Cambridge University Press:  26 October 2020

NADAV MEIR Open the ORCID record for NADAV MEIR [Opens in a new window]
NADAV MEIR*
Affiliation:
DEPARTMENT OF MATHEMATICS BEN GURION UNIVERSITY OF THE NEGEV P.O.B. 653, BE’ER SHEVA 8410501, ISRAEL and INSTYTUT MATEMATYCZNY, UNIWERSYTET WROCŁAWSKI PL. GRUNWALDZKI 2/4, 50-384 WROCŁAW, POLAND E-mail: mein@math.bgu.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an example of two ordered structures 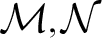$\mathcal {M},\mathcal {N}$ in the same language 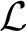$\mathcal {L}$ with the same universe, the same order and admitting the same one-variable definable subsets such that $\mathcal {M}$ is a model of the common theory of o-minimal 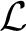$\mathcal {L}$ -structures and $\mathcal {N}$ admits a definable, closed, bounded, and discrete subset and a definable injective self-mapping of that subset which is not surjective. This answers negatively two question by Schoutens; the first being whether there is an axiomatization of the common theory of o-minimal structures in a given language by conditions on one-variable definable sets alone. The second being whether definable completeness and type completeness imply the pigeonhole principle. It also partially answers a question by Fornasiero asking whether definable completeness of an expansion of a real closed field implies the pigeonhole principle.

Keywords

definably completetype completepseudo-o-minimalo-minimalismpigeonhole principle

MSC classification

Primary: 03C10: Quantifier elimination, model completeness and related topics
Secondary: 03C35: Categoricity and completeness of theories 05D10: Ramsey theory 05C55: Generalized Ramsey theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 2 , June 2021 , pp. 577 - 599
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

The second affiliation for the author of the article has been corrected. An erratum detailing this change has also been published (doi: 10.1017/jsl.2021.100).

References

Čech, E., Bodové množiny, Academia Nakladatelství Československé Akademie Věd, Prague, 1966.Google Scholar
Fornasiero, A., Locally o-minimal structures and structures with locally o-minimal open core . Annals of Pure and Applied Logic , vol. 164 (2013), no. 3, pp. 211–229.CrossRefGoogle Scholar
Fornasiero, A., Tame structures and open cores, preprint, 2010, arXiv:1003.3557 Google Scholar
Fornasiero, A. and Hieronymi, P., A fundamental dichotomy for definably complete expansions of ordered fields, this Journal, vol. 80 (2015), no. 4, pp. 1091–1115.Google Scholar
Fornasiero, A. and Servi, T., Relative Pfaffian closure for definably complete Baire structures . Illinois Journal of Mathematics , vol. 55 (2011), no. 3, pp. 1203–1219.CrossRefGoogle Scholar
Hieronymi, P., Expansions of subfields of the real field by a discrete set . Fundamenta Mathematicae , vol. 215 (2011), no. 2, pp. 167–175.CrossRefGoogle Scholar
Hieronymi, P., An analogue of the Baire category theorem, this Journal, vol. 78 (2013), no. 1, pp. 207–213.Google Scholar
Huntington, E. V., Inter-relations among the four principal types of order . Transactions of the American Mathematical Society , vol. 38 (1935), no. 1, pp. 1–9.CrossRefGoogle Scholar
Miller, C., Expansions of dense linear orders with the intermediate value property, this Journal, vol. 66 (2001), no. 4, pp. 1783–1790.Google Scholar
Novák, V., Cuts in cyclically ordered sets . Czechoslovak Mathematical Journal , vol. 34 (1984), no. 2, pp. 322–333.CrossRefGoogle Scholar
Rennet, A., The non-axiomatizability of o-minimality, this Journal, vol. 79 (2014), no. 1, pp. 54–59.Google Scholar
Schoutens, H., o-minimalism, this Journal, vol. 79 (2014), no. 2, pp. 355–409.Google Scholar