Article contents
Recursion theory on orderings. I. A model theoretic setting1
Published online by Cambridge University Press: 12 March 2014
Extract
In [6], Metakides and Nerode introduced the study of the lattice of recursively enumerable substructures of a recursively presented model as a means to understand the recursive content of certain algebraic constructions. For example, the lattice of recursively enumerable subspaces, 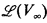 , of a recursively presented vector space V∞ has been studied by Kalantari, Metakides and Nerode, Retzlaff, Remmel and Shore. Similar studies have been done by Remmel [12], [13] for Boolean algebras and by Metakides and Nerode [9] for algebraically closed fields. In all of these models, the algebraic closure of a set is nontrivial. (The formal definition of the algebraic closure of a set S, denoted cl(S), is given in §1, however in vector spaces, cl(S) is just the subspace generated by S, in Boolean algebras, cl(S) is just the subalgebra generated by S, and in algebraically closed fields, cl(S) is just the algebraically closed subfield generated by S.)
, of a recursively presented vector space V∞ has been studied by Kalantari, Metakides and Nerode, Retzlaff, Remmel and Shore. Similar studies have been done by Remmel [12], [13] for Boolean algebras and by Metakides and Nerode [9] for algebraically closed fields. In all of these models, the algebraic closure of a set is nontrivial. (The formal definition of the algebraic closure of a set S, denoted cl(S), is given in §1, however in vector spaces, cl(S) is just the subspace generated by S, in Boolean algebras, cl(S) is just the subalgebra generated by S, and in algebraically closed fields, cl(S) is just the algebraically closed subfield generated by S.)
In this paper, we give a general model theoretic setting (whose precise definition will be given in §1) in which we are able to give constructions which generalize many of the constructions of classical recursion theory. One of the main features of the models 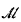 which we study is that the algebraic closure of set
which we study is that the algebraic closure of set 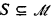 is just itself, i.e., cl(S) = S. Examples of such models include the natural numbers under equality 〈N, = 〉, the rational numbers under the usual ordering 〈Q, ≤〉, and a large class of n-dimensional partial orderings.
is just itself, i.e., cl(S) = S. Examples of such models include the natural numbers under equality 〈N, = 〉, the rational numbers under the usual ordering 〈Q, ≤〉, and a large class of n-dimensional partial orderings.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1979
Footnotes
We wish to acknowledge many helpful conversations with A. Nerode.
Supported under NSF Grant MCS77–0421.
References
REFERENCES
- 7
- Cited by

