Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-10T05:42:32.332Z Has data issue: false hasContentIssue false
  • English
  • Français

R-maximal Boolean algebras

Published online by Cambridge University Press:  12 March 2014

J. B. Remmel
Get access Rights & Permissions [Opens in a new window]

Extract

Metakides and Nerode in [2] suggested the study of what they termed the lattice of recursively enumerable substructures of a recursively presented model. For example, Metakides and Nerode in [3] introduced the lattice of of recusively enumerable subspaces, 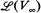, of a recursively presented vector space V∞. The similarities and differences between 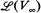and ℰ, the lattice of recursively enumerable subsets of the natural numbers N as defined in [9], have been studied by Metakides and Nerode, Kalantari, Remmel, Retzlaff, and Shore. In [6], we studied some similarities and differences between ℰ and the lattice of recursively enumerable sub-algebras of a weakly recursively presented Boolean algebra and this paper continues that study. A weakly recursively presented Boolean algebra (W.R.P.B.A.), 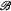, consists of a recursive subset of N, ∣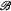∣, called the field of 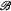, and operations 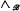(meet), 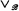(join), and 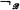(complement) which are partial recursive and under which 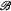becomes a Boolean algebra. We shall write 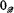and 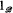for the zero and unit of 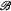. If S is a subset of 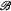, we let (S)* denote the subalgebra generated by S. Given sub-algebras B and C of 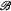, we let B + C denote (B ⋃ C)*. A subalgebra B of 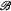is recursively enumerable (recursive) if {x ∈ ∣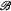∣ x ∈ B} is a recursively enumerable (recursive) subset of ∣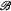∣. The set of all recursively enumerable subalgebras of 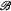, , 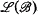forms a lattice under the operations of intersection and sum (+).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 4 , December 1979 , pp. 533 - 548
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Lachlan, A. H., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–27.CrossRefGoogle Scholar
[2]Metakides, G. and Nerode, A., Recursion theory and algebra, Algebra and logic, Lecture Notes in Mathematics, No. 450, Springer-Verlag, Berlin and New York, 1975, pp. 209–219.CrossRefGoogle Scholar
[3]Metakides, G. and Nerode, A., Recursively enumerable vector spaces, Annals of Mathematical Logic (to appear).Google Scholar
[4]Metakides, G. and Remmel, J. B., Recursion theory on orderings, this Journal (to appear).Google Scholar
[5]Remmel, J. B., Complementation in the lattice of subalgebras of a Boolean algebra, Algebra Universalis (to appear).Google Scholar
[6]Remmel, J. B., Recursively enumerable Boolean algebras, Annals of Mathematical Logic (to appear).Google Scholar
[7]Remmel, J. B., A r-maximal vector space not contained in any maximal vector space, this Journal, vol. 43(1978), pp. 430–441.Google Scholar
[8]Robinson, R. W., Simplicity of recursively enumerable sets, this Journal, vol. 32(1967), pp. 162–172.Google Scholar
[9]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[10]Sikorski, R., Boolean algebras, 2nd edition, Academic Press, New York, 1964.Google Scholar
[11]Vaught, R. L., Topics in the theory of arithmetical classes and Boolean algebras, Ph.D. Thesis, University of California, Berkeley, 1954.Google Scholar