Article contents
Sets equipollent to their power set in NF
Published online by Cambridge University Press: 12 March 2014
Extract
In this note we define a class of properties for which the following holds: If we can prove in NF that the property holds for the universe V, then we can prove in NF that it holds for every set equipollent to its power set.
Definition. For any stratified formula A and any variable υ which does not occur in A, let Aυ be the formula obtained by replacing in A each quantifier (Qx) by the bounded quantifier (Qx ∈ SCi(υ)), where i is the type of x in A. We will say that a property P(υ) is typed when there is a stratified sentence S such that P(υ) ↔ Sυ holds in NF.
Examples of typed properties are: “υ is Dedekind-infinite”, “υ is not well-orderable”. Specker [3] proved that these typed properties hold for the universe V, and C. Ward Henson [1] extended this result to any set equipollent to its power set. We will show that such an extension holds for any typed property.
Theorem. For any typed property P(υ):
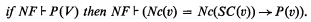
Proof. Fix a bijective map h: υ → SC(υ) and define for i = 0, 1, 2, …, n, … a bijective map hi: υ → SCi(υ) as follows:
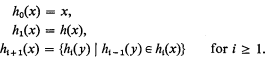
For every formula A, let A(h) be obtained by replacing in A each atomic part (x ∈ y) by (x ∈ h(y)) and each quantifier (Qx) by (Qx ∈ υ).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1975
References
REFERENCES
- 2
- Cited by

