Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T23:31:10.307Z Has data issue: false hasContentIssue false
  • English
  • Français

A Spector-Gandy theorem for cPCd(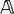) classes

Published online by Cambridge University Press:  12 March 2014

Shaughan Lavine
Shaughan Lavine*
Affiliation:
Department of Philosophy, Columbia University, New York, New York 10027
Get access Rights & Permissions [Opens in a new window]

Abstract

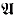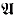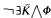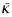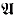Let be an admissible structure. A cPCd() class is the class of all models of a sentence of the form , where is an -r.e. set of relation symbols and Φ is an 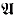-r.e. set of formulas of ℒ∞,ω that are in 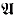. The main theorem is a generalization of the following: Let 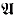be a pure countable resolvable admissible structure such that 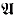is not Σ-elementarily embedded in HYP(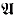). Then a class K of countable structures whose universes are sets of urelements is a cPCd(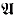) class if and only if for some Σ formula σ (with parameters from 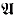), 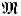is in K if and only if 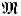is a countable structure with universe a set of urelements and 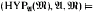σ, where 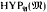, the smallest admissible set above 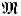relative to 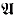, is a generalization of HYP to structures with similarity type Σ over 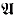that is defined in this article. Here we just note that when Lα is admissible, HYPLα(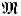) is Lβ(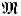) for the least β ≥ α such that Lβ(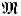) is admissible, and so, in particular, that 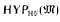is just HYP(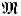) in the usual sense when 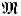has a finite similarity type.

The definition of 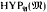is most naturally formulated using Adamson's notion of a +-admissible structure (1978). We prove a generalization from admissible to +-admissible structures of the well-known truncation lemma. That generalization is a key theorem applied in the proof of the generalized Spector-Gandy theorem.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 2 , June 1992 , pp. 478 - 500
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ada78]Adamson, Alan, Admissible sets and the saturation of structures, Annals of Mathematical Logic, vol. 14, pp. 111–157.CrossRefGoogle Scholar
[Bar75]Barwise, Jon, Admissible sets and structures, Springer-Verlag, Berlin.Google Scholar
[BGM71]Barwise, K. J., Gandy, R. O., and Moschovakis, Y. N., The next admissible set, this Journal, vol. 36, pp. 108–120.Google Scholar
[CK73]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam.Google Scholar
[CV58]Craig, W. and Vaught, R., Finite axiomatizability using additional predicates, this Journal, vol. 23, pp. 289–308.Google Scholar
[Ers86]Ershov, Yu. L., Σ-admissible sets, Akademiya Nauk SSSR Sibirskoe Otdelenie lnstitut Matematiki Vychislitel'nye Sistemy Sbornik Trudov, vyp. 138, pp. 35–39. (Russian) See M. S. Burgin, Mathematical Reviews 88k: 03080.Google Scholar
[Gan60]Gandy, R. O., Proof of Mostowski's conjecture, Bulletin de l'Académie Polonaise des Sciences, Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 8, pp. 571–575.Google Scholar
[Hin78]Hinman, Peter G., Recursion-theoretic hierarchies, Springer-Verlag, Berlin.Google Scholar
[Kle52]Kleene, S. C., Finite axiomatizability of theories in the predicate calculus using additional predicate symbols, Memoirs of the American Mathematical Society, no. 10, pp. 27–68.Google Scholar
[Lav85]Lavine, Shaughan, A Spector-Gandy theorem for model classes that are cPCd over an admissible set, this Journal, vol. 50, p. 1096 (abstract).Google Scholar
[Lav88]Lavine, Shaughan “Lavine, Michael A.”, Spector-Gandy and generalized reduction theorems for model-theoretic analogs of the class of coanalytic sets, Ph.D. thesis, University of California, Berkeley, California.Google Scholar
[Lav?]Lavine, Shaughan, Generalized reduction theorems for model-theoretic analogs of the class of coanalytic sets, this Journal (to be published).Google Scholar
[Mak64]Makkai, M., On PC⊿-classes in the theory of models, A Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei (Budapest), vol. 9, pp. 159–194.Google Scholar
[Mak77]Makkai, M., Admissible sets and infinitary logic, Chapter A.7 in Handbook of mathematical logic (Barwise, Jon, editor), North-Holland, Amsterdam, pp. 233–281.Google Scholar
[NS77]Nadel, Mark and Stavi, Jonathan, The pure part of HYP(M), this Journal, vol. 42, pp. 33–46.Google Scholar
[Res77]Ressayre, J. P., Models with compactness properties relative to an admissible language, Annals of Mathematical Logic, vol. 11, pp. 31–55.CrossRefGoogle Scholar
[Spe60]Spector, C., Hyperarithmetical quantifiers, Fundamenta Mathematicae, vol. 48, pp. 313–320.CrossRefGoogle Scholar
[Vau73]Vaught, Robert, Descriptive set theory on Lω1ω, Cambridge summer school in mathematical logic (Mathias, A. R. D. and Rogers, H., editors), Lecture Notes in Mathematics, vol. 337, Springer-Verlag, Berlin, pp. 574–598.CrossRefGoogle Scholar