Hostname: page-component-7f64f4797f-zzvtc Total loading time: 0 Render date: 2025-11-04T13:45:51.968Z Has data issue: false hasContentIssue false
  • English
  • Français

THE STRUCTURAL COMPLEXITY OF MODELS OF ARITHMETIC

Part of: Model theory Set theory Nonstandard models

Published online by Cambridge University Press:  29 June 2023

ANTONIO MONTALBÁN  and
DINO ROSSEGGER Open the ORCID record for DINO ROSSEGGER [Opens in a new window]
ANTONIO MONTALBÁN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA, BERKELEY BERKELEY, CA, USA E-mail: antonio@math.berkeley.edu
DINO ROSSEGGER*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA, BERKELEY BERKELEY, CA, USA INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY TECHNISCHE UNIVERSITÄT WIEN VIENNA, AUSTRIA
*
E-mail: dino@math.berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We calculate the possible Scott ranks of countable models of Peano arithmetic. We show that no non-standard model can have Scott rank less than 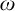$\omega $ and that non-standard models of true arithmetic must have Scott rank greater than 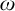$\omega $. Other than that there are no restrictions. By giving a reduction via 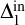$\Delta ^{\mathrm {in}}_{1}$ bi-interpretability from the class of linear orderings to the canonical structural 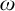$\omega $-jump of models of an arbitrary completion T of 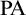$\mathrm {PA}$ we show that every countable ordinal $\alpha>\omega $ is realized as the Scott rank of a model of T.

Keywords

arithmeticScott rankPeano arithmeticnonstandard models

MSC classification

Primary: 03E15: Descriptive set theory 03C62: Models of arithmetic and set theory 03H15: Nonstandard models of arithmetic

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 4 , December 2024 , pp. 1703 - 1719
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alvir, R., Greenberg, N., Harrison-Trainor, M., and Turetsky, D., Scott complexity of countable structures, this Journal, vol. 86 (2021), no. 4, pp. 1706–1720.Google Scholar
Alvir, R. and Rossegger, D., The complexity of Scott sentences of scattered linear orders, this Journal, vol. 85 (2020), no. 3, pp. 1079–1101.Google Scholar
Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, Elsevier, Amsterdam, 2000.Google Scholar
Ash, C., Knight, J., Manasse, M., and Slaman, T., Generic copies of countable structures . Annals of Pure and Applied Logic, vol. 42 (1989), no. 3, pp. 195–205.CrossRefGoogle Scholar
Ash, C. J., Recursive labelling systems and stability of recursive structures in hyperarithmetical degrees . Transactions of the American Mathematical Society, vol. 298 (1986), no. 2, pp. 497–514.CrossRefGoogle Scholar
Barwise, J., Back and forth through infinitary logic . Studies in Model Theory, vol. 8 (1973), pp. 5–34.Google Scholar
Chisholm, J., Effective model theory vs. recursive model theory, this Journal, vol. 55 (1990), no. 3, pp. 1168–1191.Google Scholar
Coskey, S. and Kossak, R., The complexity of classification problems for models of arithmetic . Bulletin of Symbolic Logic, vol. 16 (2010), no. 3, pp. 345–358.CrossRefGoogle Scholar
Gaifman, H., Models and types of Peano’s arithmetic . Annals of Mathematical Logic, vol. 9 (1976), no. 3, pp. 223–306.CrossRefGoogle Scholar
Gonzalez, D. and Rossegger, D., Scott sentence complexities of linear orderings, submitted, 2023, arXiv:2305.07126.CrossRefGoogle Scholar
Harrison-Trainor, M., Miller, R., and Montalbán, A., Borel functors and infinitary interpretations, this Journal, vol. 83 (2018), no. 4, pp. 1434–1456.Google Scholar
Karp, C. R., Finite-quantifier equivalence , The Theory of Models, Proceedings of the 1963 International Symposium at Berkeley, North-Holland, Amsterdam, 1965, pp. 407–412.Google Scholar
Kossak, R. and Schmerl, J., The Structure of Models of Peano Arithmetic, Oxford Logic Guides, vol. 50, Oxford University Press, Oxford, 2006.CrossRefGoogle Scholar
Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas. Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.Google Scholar
Makkai, M., An example concerning Scott heights, this Journal, vol. 46 (1981), no. 2, pp. 301–318.Google Scholar
Montalbán, A., Notes on the jump of a structure , Mathematical Theory and Computational Practice (K. Ambos-Spies, B. Löwe, and W. Merkle, editors), Springer, Berlin, 2009, pp. 372–378.CrossRefGoogle Scholar
Montalbán, A., A robuster Scott rank . Proceedings of the American Mathematical Society, vol. 143 (2015), no. 12, pp. 5427–5436.CrossRefGoogle Scholar
Montalbán, A., Computable structure theory: Beyond the arithmetic, draft, 2023.Google Scholar
Montalbán, A., Computable Structure Theory: Within the Arithmetic, Cambridge University Press, Cambridge, 2021.CrossRefGoogle Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers , The Theory of Models (J. W. Addison, L. Henkin, and A. Tarski, editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, vol. 1 , Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Vaught, R., Invariant sets in topology and logic . Fundamenta Mathematicae, vol. 82 (1974), pp. 269–294.CrossRefGoogle Scholar