Article contents
Systems of notations and the ramified analytical hierarchy
Published online by Cambridge University Press: 12 March 2014
Extract
The purpose of this paper is to show that arithmetically minimal systems of notations can be constructed which provide notations for all ramified analytical ordinals (all the ordinals in the minimum β-model for analysis). This is a much larger section of the second number class than the Church-Kleene constructive ordinals (although still only an initial segment of the 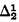 ordinals). Arithmetic minimality means that if H is an “H-set” associated with an ordinal α in our system and H′ is an H-set associated with the same ordinal α in an arbitrary system of notations S, then H is arithmetical in H′. Thus the arithmetical degrees associated with ordinals in our system are as low as possible.
ordinals). Arithmetic minimality means that if H is an “H-set” associated with an ordinal α in our system and H′ is an H-set associated with the same ordinal α in an arbitrary system of notations S, then H is arithmetical in H′. Thus the arithmetical degrees associated with ordinals in our system are as low as possible.
In order to clarify the structure of degrees of unsolvability and, more generally, to gain a deeper insight into the power set of the integers, coarser but neater classifications than the structure of Turing degrees have been sought. Several hierarchies of sets of integers have been studied, each of which organizes a certain class of sets (or their degrees of unsolvability) into a well-ordering of levels with increasing complexity of nonrecursiveness appearing at each new level. The best known of these hierarchies is the Kleene hierarchy of arithmetical sets.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 1
- Cited by

