Article contents
A transfer principle in harmonic analysis1
Published online by Cambridge University Press: 12 March 2014
Extract
Let G be a locally compact abelian group, Γ its dual group, and μ its Haar measure. For a function f: G → C, the Fourier transform 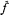 of f is defined by
of f is defined by
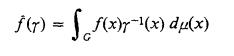
for every γ ∈ Γ.
We extend this definition for a function f on G, whose values are pairwise commutable normal operators in a Hilbert space. Then we study harmonic analysis for this extended Fourier transform.
Our method is Boolean valued analysis as introduced in [11] and [12]. Instead of developing the theory in a step-by-step manner, we shall develop a general machinery showing how to transform classical theorems to theorems in our situation.
In Chapter 1, we summarize the basic knowledge on Hilbert space, on Boolean valued model of set theory, and on Boolean valued analysis. In Chapter 2, we develop the theory of integration. Since we deal with unbounded operators as well as bounded operators, we need a new theory of integration. For a separable Hilbert space, the value of our integration coincides with the value of the usual integration with an adequate generalization for unbounded operators.
In Chapter 3, we establish machinery for our transfer principle and carry out the transformation of many classical theorems to theorems for our case.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1979
Footnotes
An article based on an invited address delivered to the Association for Symbolic Logic in Houston, Texas on April 7, 1978.
References
REFERENCES
- 19
- Cited by

