Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T17:31:59.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Upper bounds on locally countable admissible initial segments of a Turing degree hierarchy1

Published online by Cambridge University Press:  12 March 2014

Harold T. Hodes
Harold T. Hodes*
Affiliation:
Cornell University, Ithaca, New York 14853
Get access Rights & Permissions [Opens in a new window]

Abstract

Where AR is the set of arithmetic Turing degrees, 0(ω) is the least member of {a(2) ∣ a is an upper bound on AR}. This situation is quite different if we examine HYP, the set of hyperarithmetic degrees. We shall prove (Corollary 1) that there is an a, an upper bound on HYP, whose hyperjump is the degree of Kleene's 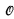. This paper generalizes this example, using an iteration of the jump operation into the transfinite which is based on results of Jensen and is detailed in [3] and [4]. In § 1 we review the basic definitions from [3] which are needed to state the general results.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 46 , Issue 4 , December 1981 , pp. 753 - 760
Copyright
Copyright © Association for Symbolic Logic 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

While writing this paper, the author was supported by a fellowship from the Mellon Foundation.

References

REFERENCES

[1]Barwise, J.; Admissible sets and structures, Springer-Verlag, Berlin and New York, 1975.CrossRefGoogle Scholar
[2]Hodes, H., Jumping through the transfinite, Ph.D. thesis, Harvard University, 1976.Google Scholar
[3]Hodes, H., Jumping through the transfinite: The master code hierarchy of Turing degrees, this Journal, vol. 45 (1980), pp. 204–220.Google Scholar
[4]Jockusch, C. and Simpson, S., A theoretic characterization of the ramified analytical hierarchy, Annals of Mathematical Logic, vol. 10 (1976).CrossRefGoogle Scholar
[5]Enderton, H.B. and Putnam, H., A note on the hyperarithmetical hierarchy, this Journal, vol. 35 (1970), pp. 429–430.Google Scholar