A version of o-minimality for the p-adics

Extract

In this paper we formulate a notion similar to o-minimality but appropriate for the p-adics. The paper is in a sense a sequel to [11] and [5]. In [11] a notion of minimality was formulated, as follows. Suppose that L, L⁺ are first-order languages and 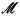⁺ is an L⁺-structure whose reduct to L is 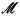. Then 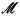⁺ is said to be 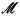-minimal if, for every N⁺ elementarily equivalent to 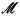⁺, every parameterdefinable subset of its domain N⁺ is definable with parameters by a quantifier-free L-formula. Observe that if L has a single binary relation which in 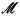is interpreted by a total order on M, then we have just the notion of strong o-minimality, from [13]; and by a theorem from [6], strong o-minimality is equivalent to o-minimality. If L has no relations, functions, or constants (other than equality) then the notion is just strong minimality.

In [11], 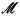-minimality is investigated for a number of structures 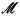. In particular, the C-relation of [1] was considered, in place of the total order in the definition of strong o-minimality. The C-relation is essentially the ternary relation which naturally holds on the maximal chains of a sufficiently nice tree; see [1], [11] or [5] for more detail, and for axioms. Much of the motivation came from the observation that a C-relation on a field F which is preserved by the affine group AGL(1,F) (consisting of permutations (a,b) : x ↦ ax + b, where a ∈ F \ {0} and b ∈ F) is the same as a non-trivial valuation: to get a C-relation from a valuation ν, put C(x;y,z) if and only if ν(y − x) < ν(y − z).