Article contents
A very weak square principle
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we explicate a very weak version of the principle □ discovered by Jensen who proved it holds in the constructible universe L. This principle is strong enough to include many of the known applications of □, but weak enough that it is consistent with the existence of very large cardinals. In this section we show that this principle is equivalent to a common combinatorial device, which we call a Jensen matrix. In the second section we show that our principle is consistent with a supercompact cardinal. In the third section of this paper we show that this principle is exactly equivalent to the statement that every torsion free Abelian group has a filtration into σ-balanced subgroups. In the fourth section of this paper we show that this principle fails if you assume the Chang's Conjecture:
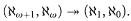
In the fifth section of the paper we review the proofs that the various weak squares we consider are strictly decreasing in strength. Section 6 was added in an ad hoc manner after the rest of the paper was written, because the subject matter of Theorem 6.1 fit well with the rest of the paper. It deals with a principle dubbed “Not So Very Weak Square”, which appears close to Very Weak Square but turns out not to be equivalent.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 64
- Cited by

