Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Finkel, Olivier
2001.
Topological properties of omega context-free languages.
Theoretical Computer Science,
Vol. 262,
Issue. 1-2,
p.
669.
Finkel, Olivier
2001.
Wadge hierarchy of omega context-free languages.
Theoretical Computer Science,
Vol. 269,
Issue. 1-2,
p.
283.
Duparc, J.
Finkel, O.
and
Ressayre, J.-P.
2001.
Computer science and the fine structure of Borel sets.
Theoretical Computer Science,
Vol. 257,
Issue. 1-2,
p.
85.
Finkel, Olivier
2001.
Computer Science Logic.
Vol. 2142,
Issue. ,
p.
369.
Duparc, J.
2003.
A hierarchy of deterministic context-free ω-languages.
Theoretical Computer Science,
Vol. 290,
Issue. 3,
p.
1253.
Duparc, Jacques
2003.
Computer Science Logic.
Vol. 2803,
Issue. ,
p.
183.
Finkel, Olivier
2003.
Ambiguity in omega context free languages.
Theoretical Computer Science,
Vol. 301,
Issue. 1-3,
p.
217.
Finkel, Olivier
2003.
On omega context free languages which are Borel sets of infinite rank.
Theoretical Computer Science,
Vol. 299,
Issue. 1-3,
p.
327.
Finkel, Olivier
2003.
Borel hierarchy and omega context free languages.
Theoretical Computer Science,
Vol. 290,
Issue. 3,
p.
1385.
Becher, Verónica
and
Grigorieff, Serge
2004.
Recursion and topology on 2⩽ω for possibly infinite computations.
Theoretical Computer Science,
Vol. 322,
Issue. 1,
p.
85.
Serre, Olivier
2004.
Automata, Languages and Programming.
Vol. 3142,
Issue. ,
p.
1150.
Selivanov, Victor L.
2005.
Variations on Wadge Reducibility Extended Abstract.
Electronic Notes in Theoretical Computer Science,
Vol. 120,
Issue. ,
p.
159.
Finkel, Olivier
2005.
New Computational Paradigms.
Vol. 3526,
Issue. ,
p.
129.
Bradfield, Julian
Duparc, Jacques
and
Quickert, Sandra
2005.
Computer Science Logic.
Vol. 3634,
Issue. ,
p.
384.
Serre, Olivier
2006.
Games with winning conditions of high Borel complexity.
Theoretical Computer Science,
Vol. 350,
Issue. 2-3,
p.
345.
Finkel, Olivier
and
Lecomte, Dominique
2007.
Computer Science Logic.
Vol. 4646,
Issue. ,
p.
115.
Duparc, Jacques
and
Murlak, Filip
2007.
Fundamentals of Computation Theory.
Vol. 4639,
Issue. ,
p.
261.
Duparc, Jacques
and
Facchini, Alessandro
2008.
Logic and Theory of Algorithms.
Vol. 5028,
Issue. ,
p.
186.
Finkel, Olivier
2008.
Topological complexity of locally finite ω-languages.
Archive for Mathematical Logic,
Vol. 47,
Issue. 6,
p.
625.
Cabessa, Jérémie
and
Duparc, Jacques
2008.
Logic and Theory of Algorithms.
Vol. 5028,
Issue. ,
p.
100.

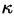 . We obtain a “normal form” of
. We obtain a “normal form” of 