Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rathjen, Michael
2011.
2010 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquium '10.
The Bulletin of Symbolic Logic,
Vol. 17,
Issue. 2,
p.
272.
Koepke, Peter
and
Welch, Philip D.
2011.
Models of Computation in Context.
Vol. 6735,
Issue. ,
p.
152.
Welch, P.D.
2014.
Turing's Legacy.
p.
493.
Montalbán, Antonio
and
Shore, Richard A.
2014.
The limits of determinacy in second order arithmetic: consistency and complexity strength.
Israel Journal of Mathematics,
Vol. 204,
Issue. 1,
p.
477.
Ackerman, Nathanael L.
Freer, Cameron E.
and
Lubarsky, Robert S.
2015.
Feedback Turing Computability, and Turing Computability as Feedback.
p.
523.
Hachtman, Sherwood
2017.
Determinacy in third order arithmetic.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 11,
p.
2008.
YOSHII, Keisuke
2017.
A Survey of Determinacy of Infinite Games in Second Order Arithmetic.
Annals of the Japan Association for Philosophy of Science,
Vol. 25,
Issue. 0,
p.
35.
Le Sueur, Chris
2018.
Determinacy of refinements to the difference hierarchy of co-analytic sets.
Annals of Pure and Applied Logic,
Vol. 169,
Issue. 1,
p.
83.
WELCH, PHILIP D.
2018.
THE RAMIFIED ANALYTICAL HIERARCHY USING EXTENDED LOGICS.
The Bulletin of Symbolic Logic,
Vol. 24,
Issue. 3,
p.
306.
Carl, Merlin
Ouazzani, Sabrina
and
Welch, Philip
2018.
Sailing Routes in the World of Computation.
Vol. 10936,
Issue. ,
p.
126.
Hachtman, Sherwood
2019.
Determinacy and monotone inductive definitions.
Israel Journal of Mathematics,
Vol. 230,
Issue. 1,
p.
71.
Bruni, Riccardo
and
Standefer, Shawn
2019.
Guest Editors’ Introduction.
Journal of Philosophical Logic,
Vol. 48,
Issue. 1,
p.
1.
Welch, Philip
2019.
Computing with Foresight and Industry.
Vol. 11558,
Issue. ,
p.
72.
Aguilera, J. P.
2021.
Long Borel Games.
Israel Journal of Mathematics,
Vol. 243,
Issue. 1,
p.
273.
Aguilera, J. P.
2023.
Locally hyperarithmetical induction.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 2,
p.
865.
AGUILERA, JUAN P.
and
LUBARSKY, ROBERT
2025.
ON WINNING STRATEGIES FOR
$F_\sigma $
GAMES.
The Journal of Symbolic Logic,
p.
1.
Aguilera, J. P.
2025.
The metamathematics of separated determinacy.
Inventiones mathematicae,

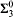 -games in the
-games in the 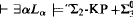 -Determinacy.”
-Determinacy.” “there is a
“there is a 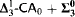 -Determinacy.” The implication is not reversible. (The antecedent here may be replaced with
-Determinacy.” The implication is not reversible. (The antecedent here may be replaced with 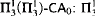 instances of Comprehension with only
instances of Comprehension with only 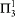 -lightface definable parameters—or even weaker theories.)
-lightface definable parameters—or even weaker theories.)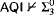 -Determinacy.
-Determinacy.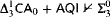 -Determinacy.
-Determinacy.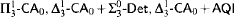 , and
, and 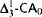 are in strictly descending order of strength.
are in strictly descending order of strength.