Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-13T07:56:24.930Z Has data issue: false hasContentIssue false
  • English
  • Français

Addendum to “A structure theorem for strongly abelian varieties”

Published online by Cambridge University Press:  12 March 2014

Bradd Hart  and
Sergei Starchenko
Bradd Hart
Affiliation:
Department of Mathematics, McMaster University, Hamilton, Ontario, CanadaL85 4K1, E-mail: bradd@billy.math.mcmaster.ca
Sergei Starchenko
Affiliation:
Department of Mathematics, Statistics and Computer Science, University of Illinoisat Chicago, Chicago IL 60637
Get access Rights & Permissions [Opens in a new window]

Extract

By a variety we mean a class of algebras in a language 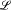, containing only function symbols, which is closed under homomorphisms, submodels, and products. A variety 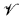is said to be strongly abelian if for any term 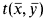in 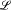, the quasi-identity

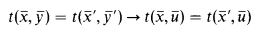
holds in .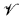

In [1] it was proved that if a strongly abelian variety has less than the maximal possible uncountable spectrum, then it is equivalent to a multisorted unary variety. Using Shelah's Main Gap theorem one can conclude that if 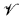is a classifiable (superstable without DOP or OTOP and shallow) strongly abelian variety then 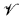is a multisorted unary variety. In fact, it was known that this conclusion followed from the assumption of superstable without DOP alone.

This paper is devoted to the proof that the superstability assumption is enough to obtain the same structure result. This fulfills a promise made in [2]. Namely, we will prove the following

Theorem 0.1. If 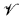is a superstable strongly abelian variety, then it is multisorted unary.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 4 , December 1993 , pp. 1419 - 1425
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hart, B. and Valeriote, M., A structure theorem for strongly abelian varieties with few models, this Journal, vol. 56 (1991), pp. 832–852.Google Scholar
[2]Hart, B., Starchenko, S., and Valeriote, M., Vaught's conjecture for varieties, Transactions of the American Mathematical Society (to appear).Google Scholar