Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T17:35:44.046Z Has data issue: false hasContentIssue false
  • English
  • Français

Addition in nonstandard models of arithmetic

Published online by Cambridge University Press:  12 March 2014

R. Phillips
R. Phillips*
Affiliation:
University of South Carolina, Columbia, South Carolina 29208
Get access Rights & Permissions [Opens in a new window]

Extract

In [3] Kemeny made the following conjecture: Suppose *Z is a nonstandard model of the ring of integers Z. Let

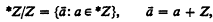
and let F be the subgroup of those cosets ā which contain an element of infinite height in *Z. Kemeny then asked if the ring R = {a: ā ∈ F} is also a nonstandard model of Z. If so then Goldbach's conjecture is false because Kemeny also shows in [3] that Goldbach's conjecture fails in R.

The papers [1] and [5] by Gandy and Mendelson show that R is not a nonstandard model of Z but we give here a simpler proof based on Mendelson's paper. Suppose R is a nonstandard model of Z. Then each positive number in R is a sum of four squares. Choose a in R so that a is a positive element of R of infinite height in *Z. Then since a is infinite in *Z, a − 1 is positive. Thus 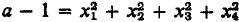, xi ∈ R for i = 1, …, 4. Now each xi must be of the form ai + ni, where ai has infinite height in *Z and ni, ∈ Z.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 3 , September 1972 , pp. 483 - 486
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Gandy, R. O., A note on a paper of Kemeny's, Mathematische Annalen, vol. 136 (1958), p. 466.CrossRefGoogle Scholar
[2]Kaplansky, I., Infinite abelian groups, University of Michigan, Ann Arbor, 1954.Google Scholar
[3]Kemeny, J. G., Undecidable problems of elementary number theory, Mathematische Annalen, vol. 135 (1958), pp. 160–169.CrossRefGoogle Scholar
[4]MacDowell, R. and Specker, E., Modelle der Arithmetik, Infinitistic methods, (Proceedings of a Symposium on Foundations of Mathematics, Warsaw, 1959), Pergamon Press, Oxford; PWN, Warsaw, 1961, pp. 257–263.Google Scholar
[5]Mendelson, E., On nonstandard models for number theory, Essays on the foundations of mathematics, Fraenkel anniversary volume, 1961, pp. 259–268.Google Scholar
[6]Phillips, R., On the structure of nonstandard models of arithmetic, Proceedings of the American Mathematical Society, vol. 27 (1971), pp. 359–363.CrossRefGoogle Scholar
[7]Robinson, A., Nonstandard analysis, Studies in logic and the foundations of mathematics, North-Holland, Amsterdam, 1966.Google Scholar