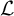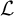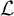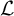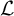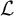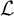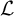1. Introduction
Continuous first-order logic was developed by Ben Yaccov and Usvyatsov in [Reference Ben Yaacov and Usvyatsov3] as a variant of the continuous logic studied by Chang and Keisler [Reference Chang and Keisler4]. This logic turns out to be very useful in the study of metric structures. For instance, Ben Yaacov [Reference Ben Yaacov1] proved that the linear isometry group of the Gurarij space is universal among all Polish groups by viewing Banach spaces as continuous first-order structures. Another example is the metric Scott analysis developed in [Reference Ben Yaacov, Doucha, Nies and Tsankov2] where the infinitary continuous first-order logic is used.
This paper is a contribution to the continuous model theory as a theory of metric structures. Previous developments of the continuous model theory have been done mostly as a generalization of the classical model theory. In this paper, we take the slightly different point of view of regarding the continuous model theory as a generalization of the rich theory of separable metric spaces.
It is well known that there is a unique complete separable metric space that is both universal (i.e., containing a copy of every separable metric space as a subspace) and ultrahomogeneous (see [Reference Urysohn18]). This space has been known as the universal Urysohn metric space and has been denoted as
![]() $\mathbb {U}$
to emphasize its canonical nature. Built on results of Katětov [Reference Katětov13], Uspenskij [Reference Uspenskij19] showed that the isometry group of
$\mathbb {U}$
to emphasize its canonical nature. Built on results of Katětov [Reference Katětov13], Uspenskij [Reference Uspenskij19] showed that the isometry group of
![]() $\mathbb {U}$
is a universal Polish group. Thus one naturally wonders whether for any continuous first-order signature
$\mathbb {U}$
is a universal Polish group. Thus one naturally wonders whether for any continuous first-order signature
![]() $\mathcal {L}$
there exists a Urysohn continuous
$\mathcal {L}$
there exists a Urysohn continuous
![]() $\mathcal {L}$
-structure, i.e., a complete separable continuous
$\mathcal {L}$
-structure, i.e., a complete separable continuous
![]() $\mathcal {L}$
-structure which is both universal and ultrahomogeneous. Moreover, if it exists, whether its automorphism group is a universal Polish group.
$\mathcal {L}$
-structure which is both universal and ultrahomogeneous. Moreover, if it exists, whether its automorphism group is a universal Polish group.
It turns out that the answer depends on the continuous first-order signature
![]() $\mathcal {L}$
. In general, a continuous first-order signature
$\mathcal {L}$
. In general, a continuous first-order signature
![]() $\mathcal {L}$
consists of relation symbols and function symbols of various arities. In this paper, we consider continuous first-order signatures
$\mathcal {L}$
consists of relation symbols and function symbols of various arities. In this paper, we consider continuous first-order signatures
![]() $\mathcal {L}$
with only finitely many relation symbols. Just as in a classical first-order signature we do not formally include the equality relation
$\mathcal {L}$
with only finitely many relation symbols. Just as in a classical first-order signature we do not formally include the equality relation
![]() $=$
but consider it to be a part of the logic, in continuous first-order logic we also tacitly include a symbol d which is always interpreted as a metric on a continuous structure. For each n-ary relation symbol
$=$
but consider it to be a part of the logic, in continuous first-order logic we also tacitly include a symbol d which is always interpreted as a metric on a continuous structure. For each n-ary relation symbol
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $1\leq i\leq n$
, we also associate a modulus of continuity
$1\leq i\leq n$
, we also associate a modulus of continuity
![]() $\mathfrak {u}_{R,i}$
. In an interpretation of R in a model (which is a function from the domain of the model to the interval
$\mathfrak {u}_{R,i}$
. In an interpretation of R in a model (which is a function from the domain of the model to the interval
![]() $[0,1]$
), R as a function of the ith coordinate is required to be a uniformly continuous function with
$[0,1]$
), R as a function of the ith coordinate is required to be a uniformly continuous function with
![]() $\mathfrak {u}_{R,i}$
as a modulus of continuity.
$\mathfrak {u}_{R,i}$
as a modulus of continuity.
We will define two notions which are properties of the moduli of continuity associated with a continuous signature
![]() $\mathcal {L}$
. They are called proper and semiproper, the difference being wether the moduli of continuity for unary relation symbols in
$\mathcal {L}$
. They are called proper and semiproper, the difference being wether the moduli of continuity for unary relation symbols in
![]() $\mathcal {L}$
(if any) are upper semicontinuous. We will prove the following theorem.
$\mathcal {L}$
(if any) are upper semicontinuous. We will prove the following theorem.
Theorem 1.1. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following hold:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following hold:
-
(i) There exists a (separable) Urysohn
 $\mathcal {L}$
-structure iff
$\mathcal {L}$
-structure iff
 $\mathcal {L}$
is proper.
$\mathcal {L}$
is proper. -
(ii) There exists a Urysohn
 $\mathcal {L}$
-pre-structure iff
$\mathcal {L}$
-pre-structure iff
 $\mathcal {L}$
is semiproper.
$\mathcal {L}$
is semiproper.
Here a continuous
![]() $\mathcal {L}$
-pre-structure is one in which the symbol d is interpreted as a metric; in contrast, in a continuous
$\mathcal {L}$
-pre-structure is one in which the symbol d is interpreted as a metric; in contrast, in a continuous
![]() $\mathcal {L}$
-structure d is interpreted as a complete metric.
$\mathcal {L}$
-structure d is interpreted as a complete metric.
It turns out that properness and semiproperness also characterize the amalgamation property for various classes of continuous
![]() $\mathcal {L}$
-structures. In particular, we have the following theorems.
$\mathcal {L}$
-structures. In particular, we have the following theorems.
Theorem 1.2. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following are equivalent:
-
(i)
 $\mathcal {L}$
is semiproper.
$\mathcal {L}$
is semiproper. -
(ii) The class of all finite continuous
 $\mathcal {L}$
-pre-structures has the amalgamation property.
$\mathcal {L}$
-pre-structures has the amalgamation property. -
(iii) The class of all finite continuous
 $\mathcal {L}$
-pre-structures has the strong amalgamation property.
$\mathcal {L}$
-pre-structures has the strong amalgamation property.
Theorem 1.3. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following are equivalent:
-
(i)
 $\mathcal {L}$
is proper.
$\mathcal {L}$
is proper. -
(ii) The class of all (countable) continuous
 $\mathcal {L}$
-pre-structures has the amalgamation property.
$\mathcal {L}$
-pre-structures has the amalgamation property. -
(iii) The class of all (countable) continuous
 $\mathcal {L}$
-pre-structures has the strong amalgamation property.
$\mathcal {L}$
-pre-structures has the strong amalgamation property.
We also define an intermediate notion of strong semiproperness between semiproperness and properness, and characterize the amalgamation property of the class of continuous
![]() $\mathcal {L}$
-structures.
$\mathcal {L}$
-structures.
Theorem 1.4. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. Then the following are equivalent:
-
(i)
 $\mathcal {L}$
is strongly semiproper.
$\mathcal {L}$
is strongly semiproper. -
(ii) The class of all (countable) continuous
 $\mathcal {L}$
-structures has the amalgamation property.
$\mathcal {L}$
-structures has the amalgamation property. -
(iii) The class of all (countable) continuous
 $\mathcal {L}$
-structures has the strong amalgamation property.
$\mathcal {L}$
-structures has the strong amalgamation property.
The separable Urysohn continuous
![]() $\mathcal {L}$
-structure will enjoy similar canonicity as its classical counterpart, and thus we denote it by
$\mathcal {L}$
-structure will enjoy similar canonicity as its classical counterpart, and thus we denote it by
![]() $\mathbb {U}_{\mathcal {L}}$
. Because
$\mathbb {U}_{\mathcal {L}}$
. Because
![]() $\mathbb {U}_{\mathcal {L}}$
is constructed with a Katětov-style construction, it will follow from Uspenskij’s argument that the automorphism group of
$\mathbb {U}_{\mathcal {L}}$
is constructed with a Katětov-style construction, it will follow from Uspenskij’s argument that the automorphism group of
![]() $\mathbb {U}_{\mathcal {L}}$
is a universal Polish group.
$\mathbb {U}_{\mathcal {L}}$
is a universal Polish group.
We will also consider certain classes of finite continuous
![]() $\mathcal {L}$
-structures for semiproper
$\mathcal {L}$
-structures for semiproper
![]() $\mathcal {L}$
and show that they are countable Fraïssé classes. In particular, we obtain a rational Urysohn continuous
$\mathcal {L}$
and show that they are countable Fraïssé classes. In particular, we obtain a rational Urysohn continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathbb {QU}_{\mathcal {L}}$
in analogy with its classical counterpart
$\mathbb {QU}_{\mathcal {L}}$
in analogy with its classical counterpart
![]() $\mathbb {QU}$
.
$\mathbb {QU}$
.
We will show that for any semiproper
![]() $\mathcal {L}$
the class of all finite continuous
$\mathcal {L}$
the class of all finite continuous
![]() $\mathcal {L}$
-structures have the coherent EPPA. EPPA stands for the Extension Property for Partial Automorphisms and is a term coined by Hrushovski when he first showed the EPPA for graphs (see [Reference Hrushovski11]). Later on, the EPPA has been proven for a great number of classes of structures, most notably for classical finite relational structures (Herwig–Lascar [Reference Herwig and Lascar10]) and for finite metric spaces (Solecki [Reference Solecki17]). For a survey of recent results on EPPA see [Reference Hubička, Konečný and Nešetřil12]. Siniora–Solecki [Reference Siniora and Solecki16] defined the coherent EPPA and proved it for a large number of classes of classical structures. Here we prove the following theorem.
$\mathcal {L}$
-structures have the coherent EPPA. EPPA stands for the Extension Property for Partial Automorphisms and is a term coined by Hrushovski when he first showed the EPPA for graphs (see [Reference Hrushovski11]). Later on, the EPPA has been proven for a great number of classes of structures, most notably for classical finite relational structures (Herwig–Lascar [Reference Herwig and Lascar10]) and for finite metric spaces (Solecki [Reference Solecki17]). For a survey of recent results on EPPA see [Reference Hubička, Konečný and Nešetřil12]. Siniora–Solecki [Reference Siniora and Solecki16] defined the coherent EPPA and proved it for a large number of classes of classical structures. Here we prove the following theorem.
Theorem 1.5. Let
![]() $\mathcal {L}$
be any semiproper continuous signature. The class of all finite continuous
$\mathcal {L}$
be any semiproper continuous signature. The class of all finite continuous
![]() $\mathcal {L}$
-structures has the coherent EPPA.
$\mathcal {L}$
-structures has the coherent EPPA.
It turns out that the (coherent) EPPA for the class of all finite continuous
![]() $\mathcal {L}$
-structures is essentially equivalent to the semiproperness of
$\mathcal {L}$
-structures is essentially equivalent to the semiproperness of
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
The method of Herwig–Lascar made deep connections between properties of free groups and extensions of partial automorphisms or group actions. These group-theoretic properties were studied further by other authors, including Coulbois [Reference Coulbois5], Rosendal [Reference Rosendal14, Reference Rosendal15], and Etedadialiabadi–Gao [Reference Etedadialiabadi and Gao6, Reference Etedadialiabadi and Gao7]. These investigations culminated in [Reference Etedadialiabadi, Gao, Le Maître and Melleray8] to show that the actions by automorphisms of finite groups on finite classical relational structures form a Fraïssé class. Here we prove an analogous result for continuous structures as follows.
Theorem 1.6. Let
![]() $\mathcal {L}$
be any semiproper continuous signature. The class of all actions by automorphisms of finite groups on finite continuous
$\mathcal {L}$
be any semiproper continuous signature. The class of all actions by automorphisms of finite groups on finite continuous
![]() $\mathcal {L}$
-structures form a Fraïssé class. Consequently, if
$\mathcal {L}$
-structures form a Fraïssé class. Consequently, if
![]() $\mathcal {L}$
is proper, the automorphism group of
$\mathcal {L}$
is proper, the automorphism group of
![]() $\mathbb {U}_{\mathcal {L}}$
contains Hall’s universal locally finite group
$\mathbb {U}_{\mathcal {L}}$
contains Hall’s universal locally finite group
![]() $\mathbb {H}$
as a dense subgroup.
$\mathbb {H}$
as a dense subgroup.
The rest of the paper is organized as follows. In Section 2 we recall some basic definitions. In Section 3 we define properness, semiproperness, and strong semiproperness for continuous first-order signatures and prove Theorems 1.2–1.4. In Section 4 we give a Katětov-style construction of the Urysohn continuous structure for a proper continuous first-order signature. In particular, we prove Theorem 1.1. In Section 5 we consider certain classes of finite continuous structures and show that they form countable Fraïssé classes. We also show that the completion of
![]() $\mathbb {QU}_{\mathcal {L}}$
is isomorphic to
$\mathbb {QU}_{\mathcal {L}}$
is isomorphic to
![]() $\mathbb {U}_{\mathcal {L}}$
when
$\mathbb {U}_{\mathcal {L}}$
when
![]() $\mathcal {L}$
is proper. In Section 6 we prove Theorem 1.5. In Section 7 we prove the first half of Theorem 1.6. For this the main effort is to prove an analog of a theorem of Rosendal on finite approximations of actions on continuous structures. In Section 8 we prove the second half of Theorem 1.6.
$\mathcal {L}$
is proper. In Section 6 we prove Theorem 1.5. In Section 7 we prove the first half of Theorem 1.6. For this the main effort is to prove an analog of a theorem of Rosendal on finite approximations of actions on continuous structures. In Section 8 we prove the second half of Theorem 1.6.
2. Preliminaries
We first recall some basic definitions in continuous first-order logic. This is mostly following [Reference Ben Yaacov and Usvyatsov3] but we do deviate at various places for the convenience of our presentation.
Definition 2.1.
-
(i) A modulus of continuity is a function
such that $$ \begin{align*}\mathfrak{u}:(0,\infty)\to (0, \infty]\end{align*} $$
$$ \begin{align*}\mathfrak{u}:(0,\infty)\to (0, \infty]\end{align*} $$
 $\lim _{\delta \to 0}\mathfrak {u}(\delta )=0$
.
$\lim _{\delta \to 0}\mathfrak {u}(\delta )=0$
.
-
(ii) Let
 $\mathfrak {u}$
be a modulus of continuity. Let
$\mathfrak {u}$
be a modulus of continuity. Let
 $(X_1, d_1)$
and
$(X_1, d_1)$
and
 $(X_2, d_2)$
be metric spaces. We say that a mapping
$(X_2, d_2)$
be metric spaces. We say that a mapping
 $f: X_1\to X_2$
is uniformly continuous with respect to
$f: X_1\to X_2$
is uniformly continuous with respect to
 $\mathfrak {u}$
(or simply that f respects
$\mathfrak {u}$
(or simply that f respects
 $\mathfrak {u}$
) if for all
$\mathfrak {u}$
) if for all
 $x, y\in X_1$
, we have
$x, y\in X_1$
, we have  $$ \begin{align*}d_2(f(x),f(y))\leq\mathfrak{u}(d_1(x,y)).\end{align*} $$
$$ \begin{align*}d_2(f(x),f(y))\leq\mathfrak{u}(d_1(x,y)).\end{align*} $$
Whenever convenient, we consider a modulus of continuity function
![]() $\mathfrak {u}$
to be defined at
$\mathfrak {u}$
to be defined at
![]() $0$
and set
$0$
and set
![]() $\mathfrak {u}(0)=0$
. Then
$\mathfrak {u}(0)=0$
. Then
![]() $\mathfrak {u}$
is continuous at
$\mathfrak {u}$
is continuous at
![]() $0$
. If f respects a modulus of continuity
$0$
. If f respects a modulus of continuity
![]() $\mathfrak {u}$
, then by redefining
$\mathfrak {u}$
, then by redefining
we get that
![]() $\mathfrak {u}'$
is nondecreasing but still a modulus of continuity that f respects. Later when we consider superadditive and upper semicontinuous moduli of continuity, this redefinition with the supremum operation can still keep the superadditivity and upper semicontinuity, respectively, and at the same time makes the modulus of continuity nondecreasing. So throughout this paper we assume that all of the moduli of continuity we consider are nondecreasing.
$\mathfrak {u}'$
is nondecreasing but still a modulus of continuity that f respects. Later when we consider superadditive and upper semicontinuous moduli of continuity, this redefinition with the supremum operation can still keep the superadditivity and upper semicontinuity, respectively, and at the same time makes the modulus of continuity nondecreasing. So throughout this paper we assume that all of the moduli of continuity we consider are nondecreasing.
Definition 2.2.
-
(i) A function
 $u:[a, b]\to \mathbb {R}$
is subadditive if for all
$u:[a, b]\to \mathbb {R}$
is subadditive if for all
 $x, y\in [a, b]$
, if
$x, y\in [a, b]$
, if
 $x+y\in [a, b]$
, then
$x+y\in [a, b]$
, then  $$ \begin{align*}u(x+y)\leq u(x)+u(y).\end{align*} $$
$$ \begin{align*}u(x+y)\leq u(x)+u(y).\end{align*} $$
-
(ii) A function
 $u:[a, b]\to \mathbb {R}$
is superadditive if for all
$u:[a, b]\to \mathbb {R}$
is superadditive if for all
 $x, y\in [a, b]$
, if
$x, y\in [a, b]$
, if
 $x+y\in [a, b]$
, then
$x+y\in [a, b]$
, then  $$ \begin{align*}u(x+y)\geq u(x)+u(y).\end{align*} $$
$$ \begin{align*}u(x+y)\geq u(x)+u(y).\end{align*} $$
-
(iii) A function
 $u:[a, b]\to \mathbb {R}$
is upper semicontinuous if for all
$u:[a, b]\to \mathbb {R}$
is upper semicontinuous if for all
 $x\in [a, b]$
and
$x\in [a, b]$
and
 $\epsilon>0$
, there is
$\epsilon>0$
, there is
 $\delta>0$
such that for all
$\delta>0$
such that for all
 $x'\in (x-\delta , x+\delta )\cap [a,b]$
, we have
$x'\in (x-\delta , x+\delta )\cap [a,b]$
, we have
 $u(x')<u(x)+\epsilon $
.
$u(x')<u(x)+\epsilon $
.
It is easy to see that if
![]() $u:[0, b]\to \mathbb {R}$
is superadditive and nondecreasing then u is strictly increasing. For a nondecreasing
$u:[0, b]\to \mathbb {R}$
is superadditive and nondecreasing then u is strictly increasing. For a nondecreasing
![]() $u:[a,b]\to \mathbb {R}$
, u is upper semicontinuous iff for all
$u:[a,b]\to \mathbb {R}$
, u is upper semicontinuous iff for all
![]() $x\in [a,b]$
,
$x\in [a,b]$
,
![]() $\lim _{\delta \to 0^+} u(x+\delta )=u(x)$
. The following lemma is also easy.
$\lim _{\delta \to 0^+} u(x+\delta )=u(x)$
. The following lemma is also easy.
Lemma 2.3. Let
![]() $\mathfrak {u}$
be a modulus of continuity and
$\mathfrak {u}$
be a modulus of continuity and
![]() $c>0$
be such that
$c>0$
be such that
![]() $\mathfrak {u}$
is nondecreasing and superadditive on
$\mathfrak {u}$
is nondecreasing and superadditive on
![]() $[0,c]$
. Let
$[0,c]$
. Let
![]() $a=\mathfrak {u}(c)$
. Define
$a=\mathfrak {u}(c)$
. Define
![]() $\mathfrak {u}^*:[0,a)\to [0, c]$
by
$\mathfrak {u}^*:[0,a)\to [0, c]$
by
Then
![]() $\mathfrak {u}^*(0)=0$
and
$\mathfrak {u}^*(0)=0$
and
![]() $u^*$
is a subadditive, nondecreasing, and upper semicontinuous function. Moreover,
$u^*$
is a subadditive, nondecreasing, and upper semicontinuous function. Moreover,
-
(1)
 $\mathfrak {u}^*$
is continuous at
$\mathfrak {u}^*$
is continuous at
 $0$
,
$0$
, -
(2) for all
 $r\in [0, c]$
,
$r\in [0, c]$
,
 $\mathfrak {u}^*(\mathfrak {u}(r))=r$
, and
$\mathfrak {u}^*(\mathfrak {u}(r))=r$
, and -
(3) if
 $\mathfrak {u}$
is upper semicontinuous, then for all
$\mathfrak {u}$
is upper semicontinuous, then for all
 $t\in [0,a)$
,
$t\in [0,a)$
,
 $\mathfrak {u}(\mathfrak {u}^*(t))\geq t$
.
$\mathfrak {u}(\mathfrak {u}^*(t))\geq t$
.
Definition 2.4. A continuous (first-order) signature consists of
-
(i) A specific binary predicate symbol d, known as the distance symbol.
-
(ii) A set of relation symbols, each with a finite arity, such that for each n-ary relation symbol R and for each
 $1\leq i\leq n$
there is a modulus of continuity
$1\leq i\leq n$
there is a modulus of continuity
 $\mathfrak {u}_{R,i}$
, which we call the uniform continuity modulus of R with respect to the ith argument.
$\mathfrak {u}_{R,i}$
, which we call the uniform continuity modulus of R with respect to the ith argument. -
(iii) A set of function symbols, each with a finite arity, such that for each n-ary function symbol F and for each
 $1\leq i\leq n$
there is a modulus of continuity
$1\leq i\leq n$
there is a modulus of continuity
 $\mathfrak {u}_{F,i}$
, known as the uniform continuity modulus of F with respect to the ith argument.
$\mathfrak {u}_{F,i}$
, known as the uniform continuity modulus of F with respect to the ith argument.
When we speak of a continuous signature
![]() $\mathcal {L}$
, it is customary to omit the distance symbol d and consider only the relation symbols and function symbols as elements of
$\mathcal {L}$
, it is customary to omit the distance symbol d and consider only the relation symbols and function symbols as elements of
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Definition 2.5. Let
![]() $\mathcal {L}$
be a continuous signature. A continuous
$\mathcal {L}$
be a continuous signature. A continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
is a set M together with an interpretation
$\mathcal {M}$
is a set M together with an interpretation
![]() $d^M$
for d,
$d^M$
for d,
![]() $R^M$
for every relation symbol R in
$R^M$
for every relation symbol R in
![]() $\mathcal {L}$
, and
$\mathcal {L}$
, and
![]() $F^M$
for every function symbol F in
$F^M$
for every function symbol F in
![]() $\mathcal {L}$
, such that:
$\mathcal {L}$
, such that:
-
(i)
 $d^M$
is a metric on M;
$d^M$
is a metric on M; -
(ii) for each n-ary relation symbol R,
 $R^M: M^n\to [0,1]$
is such that for each
$R^M: M^n\to [0,1]$
is such that for each
 $1\leq i\leq n$
and for all
$1\leq i\leq n$
and for all
 $x_1,\dots ,x_{i-1},y, z, x_{i+1},\dots x_n\in M$
, (UCℒ)
$x_1,\dots ,x_{i-1},y, z, x_{i+1},\dots x_n\in M$
, (UCℒ) $$\begin{align}\begin{array}{l}|R^M(x_1,\dots, x_{i-1},y,x_{i+1},\dots, x_n)- \\ \ \ \ \ \ \ \ \ \ \ R^M(x_1,\dots, x_{i-1},z,x_{i+1},\dots, x_n)| \leq \mathfrak{u}_{R,i}(d^M(y,z));\end{array} \end{align}$$
$$\begin{align}\begin{array}{l}|R^M(x_1,\dots, x_{i-1},y,x_{i+1},\dots, x_n)- \\ \ \ \ \ \ \ \ \ \ \ R^M(x_1,\dots, x_{i-1},z,x_{i+1},\dots, x_n)| \leq \mathfrak{u}_{R,i}(d^M(y,z));\end{array} \end{align}$$
-
(iii) for each n-ary function symbol F,
 $F^M: M^n\to M$
is such that for each
$F^M: M^n\to M$
is such that for each
 $1\leq i\leq n$
and for all
$1\leq i\leq n$
and for all
 $x_1,\dots ,x_{i-1},y, z, x_{i+1},\dots x_n\in M$
,
$x_1,\dots ,x_{i-1},y, z, x_{i+1},\dots x_n\in M$
,  $$ \begin{align*}\begin{array}{l} d^M(F^M(x_1,\dots, x_{i-1},y,x_{i+1},\dots, x_n), \\ \ \ \ \ \ \ \ \ \ \ F^M(x_1,\dots, x_{i-1},z,x_{i+1},\dots, x_n))\leq \mathfrak{u}_{F,i}(d^M(y,z)).\end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{l} d^M(F^M(x_1,\dots, x_{i-1},y,x_{i+1},\dots, x_n), \\ \ \ \ \ \ \ \ \ \ \ F^M(x_1,\dots, x_{i-1},z,x_{i+1},\dots, x_n))\leq \mathfrak{u}_{F,i}(d^M(y,z)).\end{array}\end{align*} $$
A continuous
![]() $\mathcal {L}$
-structure is a continuous
$\mathcal {L}$
-structure is a continuous
![]() $\mathcal {L}$
-pre-structure in which
$\mathcal {L}$
-pre-structure in which
![]() $d^M$
is a complete metric.
$d^M$
is a complete metric.
Note that in [Reference Ben Yaacov and Usvyatsov3] the interpretation
![]() $d^{M}$
in an
$d^{M}$
in an
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
can be a pseudo-metric instead of a metric. Our definition here is more restrictive. Also, in this paper we will be considering relational continuous structures, that is, those continuous
$\mathcal {M}$
can be a pseudo-metric instead of a metric. Our definition here is more restrictive. Also, in this paper we will be considering relational continuous structures, that is, those continuous
![]() $\mathcal {L}$
-structures for which the continuous signature
$\mathcal {L}$
-structures for which the continuous signature
![]() $\mathcal {L}$
does not contain function symbols. Thus only the moduli of continuity
$\mathcal {L}$
does not contain function symbols. Thus only the moduli of continuity
![]() $\mathfrak {u}_{R,i}$
for relational symbols
$\mathfrak {u}_{R,i}$
for relational symbols
![]() $R\in \mathcal {L}$
will be of interest to us. For this reason we use (UCℒ
) to denote the uniform continuity conditions only for relation symbols.
$R\in \mathcal {L}$
will be of interest to us. For this reason we use (UCℒ
) to denote the uniform continuity conditions only for relation symbols.
Definition 2.6. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {M}$
be a continuous
$\mathcal {M}$
be a continuous
![]() $\mathcal {L}$
-pre-structure. We say that
$\mathcal {L}$
-pre-structure. We say that
![]() $\mathcal {M}$
is finite, countable, separable, etc. if
$\mathcal {M}$
is finite, countable, separable, etc. if
![]() $(M, d^M)$
is finite, countable, separable, etc. respectively.
$(M, d^M)$
is finite, countable, separable, etc. respectively.
Note that a finite continuous
![]() $\mathcal {L}$
-pre-structure is necessarily a continuous
$\mathcal {L}$
-pre-structure is necessarily a continuous
![]() $\mathcal {L}$
-structure. In general, given a continuous signature
$\mathcal {L}$
-structure. In general, given a continuous signature
![]() $\mathcal {L}$
and a continuous
$\mathcal {L}$
and a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
, one may consider the completion
$\mathcal {M}$
, one may consider the completion
![]() $(\bar {M}, d^{\bar {M}})$
of
$(\bar {M}, d^{\bar {M}})$
of
![]() $(M, d^M)$
and define, for any relation symbol
$(M, d^M)$
and define, for any relation symbol
![]() $R\in \mathcal {L}$
and function symbol
$R\in \mathcal {L}$
and function symbol
![]() $F\in \mathcal {L}$
,
$F\in \mathcal {L}$
,
![]() $R^{\bar {M}}$
and
$R^{\bar {M}}$
and
![]() $F^{\bar {M}}$
naturally. However, the resulting structure might not satisfy (UCℒ
) and hence might not be a continuous
$F^{\bar {M}}$
naturally. However, the resulting structure might not satisfy (UCℒ
) and hence might not be a continuous
![]() $\mathcal {L}$
-structure. Under the assumption that all the moduli of continuity associated with
$\mathcal {L}$
-structure. Under the assumption that all the moduli of continuity associated with
![]() $\mathcal {L}$
are upper semicontinuous, one can deduce (UCℒ
) and obtain a continuous
$\mathcal {L}$
are upper semicontinuous, one can deduce (UCℒ
) and obtain a continuous
![]() $\mathcal {L}$
-structure by completion.
$\mathcal {L}$
-structure by completion.
Definition 2.7. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {N}$
be continuous
$\mathcal {N}$
be continuous
![]() $\mathcal {L}$
-pre-structures. We say that
$\mathcal {L}$
-pre-structures. We say that
![]() $\mathcal {N}$
is a substructure of
$\mathcal {N}$
is a substructure of
![]() $\mathcal {M}$
if all of the following hold:
$\mathcal {M}$
if all of the following hold:
-
(i)
 $N\subseteq M$
;
$N\subseteq M$
; -
(ii)
 $d^M\,{\!\upharpoonright \!}\,\, (N\times N)=d^N$
;
$d^M\,{\!\upharpoonright \!}\,\, (N\times N)=d^N$
; -
(iii) for each n-ary relation symbol R in
 $\mathcal {L}$
and for all
$\mathcal {L}$
and for all
 $u_1,\dots , u_n\in N$
,
$u_1,\dots , u_n\in N$
,  $$ \begin{align*}R^M(u_1,\dots, u_n)=R^N(u_1,\dots, u_n);\end{align*} $$
$$ \begin{align*}R^M(u_1,\dots, u_n)=R^N(u_1,\dots, u_n);\end{align*} $$
-
(iv) for each n-ary function symbol F in
 $\mathcal {L}$
and for all
$\mathcal {L}$
and for all
 $u_1,\dots , u_n\in N$
,
$u_1,\dots , u_n\in N$
,  $$ \begin{align*}F^M(u_1,\dots, u_n)=F^N(u_1,\dots, u_n).\end{align*} $$
$$ \begin{align*}F^M(u_1,\dots, u_n)=F^N(u_1,\dots, u_n).\end{align*} $$
When
![]() $\mathcal {N}$
is a substructure of
$\mathcal {N}$
is a substructure of
![]() $\mathcal {M}$
, we also say that
$\mathcal {M}$
, we also say that
![]() $\mathcal {M}$
is an extension of
$\mathcal {M}$
is an extension of
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
Note that in case
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are continuous
$\mathcal {N}$
are continuous
![]() $\mathcal {L}$
-structures, from the requirements of completeness of the specified metrics, it follows that the domain of a substructure
$\mathcal {L}$
-structures, from the requirements of completeness of the specified metrics, it follows that the domain of a substructure
![]() $\mathcal {N}$
is necessarily a closed subset of the domain of the ambient structure
$\mathcal {N}$
is necessarily a closed subset of the domain of the ambient structure
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Definition 2.8. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {M}, \mathcal {N}$
be continuous
$\mathcal {M}, \mathcal {N}$
be continuous
![]() $\mathcal {L}$
-pre-structures. An isomorphism from
$\mathcal {L}$
-pre-structures. An isomorphism from
![]() $\mathcal {M}$
to
$\mathcal {M}$
to
![]() $\mathcal {N}$
is a bijection
$\mathcal {N}$
is a bijection
![]() $\varphi : M\to N$
such that:
$\varphi : M\to N$
such that:
-
(i)
 $\varphi $
is an isometry from
$\varphi $
is an isometry from
 $(M, d^M)$
to
$(M, d^M)$
to
 $(N, d^N)$
;
$(N, d^N)$
; -
(ii) for each n-ary relation symbol R in
 $\mathcal {L}$
and for all
$\mathcal {L}$
and for all
 $x_1,\dots , x_n\in M$
,
$x_1,\dots , x_n\in M$
,  $$ \begin{align*}R^M(x_1,\dots, x_n)=R^N(\varphi(x_1),\dots, \varphi(x_n));\end{align*} $$
$$ \begin{align*}R^M(x_1,\dots, x_n)=R^N(\varphi(x_1),\dots, \varphi(x_n));\end{align*} $$
-
(iii) for each n-ary function symbol F in
 $\mathcal {L}$
and for all
$\mathcal {L}$
and for all
 $x_1,\dots , x_n\in M$
,
$x_1,\dots , x_n\in M$
,  $$ \begin{align*}\varphi(F^M(x_1,\dots, x_n))=F^N(\varphi(x_1),\dots, \varphi(x_n)).\end{align*} $$
$$ \begin{align*}\varphi(F^M(x_1,\dots, x_n))=F^N(\varphi(x_1),\dots, \varphi(x_n)).\end{align*} $$
An isomorphism from
![]() $\mathcal {M}$
to itself is called an automorphism. The set of all automorphisms of
$\mathcal {M}$
to itself is called an automorphism. The set of all automorphisms of
![]() $\mathcal {M}$
is denoted
$\mathcal {M}$
is denoted
![]() ${\mathrm {Aut}}(\mathcal {M})$
.
${\mathrm {Aut}}(\mathcal {M})$
.
Definition 2.9. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {M}, \mathcal {N}$
be continuous
$\mathcal {M}, \mathcal {N}$
be continuous
![]() $\mathcal {L}$
-pre-structures. An isomorphic embedding from
$\mathcal {L}$
-pre-structures. An isomorphic embedding from
![]() $\mathcal {N}$
into
$\mathcal {N}$
into
![]() $\mathcal {M}$
is an isomorphism from
$\mathcal {M}$
is an isomorphism from
![]() $\mathcal {N}$
to a substructure of
$\mathcal {N}$
to a substructure of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Definition 2.10. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {M}$
be a continuous
$\mathcal {M}$
be a continuous
![]() $\mathcal {L}$
-pre-structure. A partial isomorphism of
$\mathcal {L}$
-pre-structure. A partial isomorphism of
![]() $\mathcal {M}$
is an isomorphism p from
$\mathcal {M}$
is an isomorphism p from
![]() $\mathcal {N}_1$
to
$\mathcal {N}_1$
to
![]() $\mathcal {N}_2$
, where
$\mathcal {N}_2$
, where
![]() $\mathcal {N}_1$
and
$\mathcal {N}_1$
and
![]() $\mathcal {N}_2$
are substructures of
$\mathcal {N}_2$
are substructures of
![]() $\mathcal {M}$
. The set of all partial isomorphisms of
$\mathcal {M}$
. The set of all partial isomorphisms of
![]() $\mathcal {M}$
is denoted
$\mathcal {M}$
is denoted
![]() ${\mathrm {Part}}(\mathcal {M})$
.
${\mathrm {Part}}(\mathcal {M})$
.
3. Characterizations of amalgamation properties
Throughout the rest of the paper we consider continuous signatures with only finitely many relation symbols. In this section we give characterizations of those moduli of continuity associated with a continuous signature
![]() $\mathcal {L}$
for which the classes of finite, countable, or all continuous
$\mathcal {L}$
for which the classes of finite, countable, or all continuous
![]() $\mathcal {L}$
-structures have the amalgamation property.
$\mathcal {L}$
-structures have the amalgamation property.
We first recall the definitions of the amalgamation property and of the strong amalgamation property.
Definition 3.1. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {K}$
be a set of continuous
$\mathcal {K}$
be a set of continuous
![]() $\mathcal {L}$
-pre-structures.
$\mathcal {L}$
-pre-structures.
-
(i)
 $\mathcal {K}$
has the amalgamation property (AP) if for any
$\mathcal {K}$
has the amalgamation property (AP) if for any
 $\mathcal {M}$
,
$\mathcal {M}$
,
 $\mathcal {P}$
,
$\mathcal {P}$
,
 $\mathcal {Q}\in \mathcal {K}$
and isomorphic embeddings
$\mathcal {Q}\in \mathcal {K}$
and isomorphic embeddings
 $\varphi : \mathcal {M}\to \mathcal {P}$
and
$\varphi : \mathcal {M}\to \mathcal {P}$
and
 $\psi :\mathcal {M}\to \mathcal {Q}$
, there exist
$\psi :\mathcal {M}\to \mathcal {Q}$
, there exist
 $\mathcal {N}\in \mathcal {K}$
and isomorphic embeddings
$\mathcal {N}\in \mathcal {K}$
and isomorphic embeddings
 $\iota :\mathcal {P}\to \mathcal {N}$
and
$\iota :\mathcal {P}\to \mathcal {N}$
and
 $\tau :\mathcal {Q}\to \mathcal {N}$
such that
$\tau :\mathcal {Q}\to \mathcal {N}$
such that
 $\iota \circ \varphi =\tau \circ \psi $
, i.e., the following diagram commutes: The continuous
$\iota \circ \varphi =\tau \circ \psi $
, i.e., the following diagram commutes: The continuous
 $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
 $\mathcal {N}$
is called an amalgam of
$\mathcal {N}$
is called an amalgam of
 $\mathcal {P}$
and
$\mathcal {P}$
and
 $\mathcal {Q}$
over
$\mathcal {Q}$
over
 $\mathcal {M}$
.
$\mathcal {M}$
.
-
(ii)
 $\mathcal {K}$
has the strong amalgamation property (SAP) if in the above definition we have in addition that
$\mathcal {K}$
has the strong amalgamation property (SAP) if in the above definition we have in addition that  $$ \begin{align*}\mbox{range}(\iota)\cap\mbox{range}(\tau)=\mbox{range}(\iota\circ\varphi)=\mbox{range}(\tau\circ\psi).\end{align*} $$
$$ \begin{align*}\mbox{range}(\iota)\cap\mbox{range}(\tau)=\mbox{range}(\iota\circ\varphi)=\mbox{range}(\tau\circ\psi).\end{align*} $$
Our characterizations will involve the following definition.
Definition 3.2. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing.
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing.
-
(i)
 $\mathcal {L}$
is semiproper if:
$\mathcal {L}$
is semiproper if:-
• for any n-ary
 $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
 $1\leq i\leq n$
, is bounded, and
$1\leq i\leq n$
, is bounded, and $$ \begin{align*}I_{R,i}=\{ r\in [0,+\infty)\,:\, \mathfrak{u}_{R,i}(r)<1\}\end{align*} $$
$$ \begin{align*}I_{R,i}=\{ r\in [0,+\infty)\,:\, \mathfrak{u}_{R,i}(r)<1\}\end{align*} $$
 $\mathfrak {u}_{R,i}$
is superadditive on
$\mathfrak {u}_{R,i}$
is superadditive on
 $I_{R,i}$
; and
$I_{R,i}$
; and
-
• for any n-ary
 $R\in \mathcal {L}$
, where
$R\in \mathcal {L}$
, where
 $n\geq 2$
, and
$n\geq 2$
, and
 $1\leq i\leq n$
, there is
$1\leq i\leq n$
, there is
 $K_{R,i}>0$
such that
$K_{R,i}>0$
such that
 $\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
$\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
 $r\in I_{R,i}$
.
$r\in I_{R,i}$
.
-
-
(ii)
 $\mathcal {L}$
is proper if
$\mathcal {L}$
is proper if
 $\mathcal {L}$
is semiproper and each
$\mathcal {L}$
is semiproper and each
 $\mathfrak {u}_{R,i}$
is upper semicontinuous on
$\mathfrak {u}_{R,i}$
is upper semicontinuous on
 $I_{R,i}$
.
$I_{R,i}$
.
The amalgamation property requires a method to construct extensions of partially defined continuous structures to fully defined ones. In the following we first develop this method. For this, we fix a continuous signature
![]() $\mathcal {L}$
with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing.
$\mathcal {L}$
with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing.
Definition 3.3. Let
![]() $(X, d^X)$
be a metric space and
$(X, d^X)$
be a metric space and
![]() $\mathfrak {u}$
be a nondecreasing modulus of continuity. For any
$\mathfrak {u}$
be a nondecreasing modulus of continuity. For any
![]() $x, y\in X$
, define a pseudo-metric on X by
$x, y\in X$
, define a pseudo-metric on X by
 $$ \begin{align*} d^X_{\mathfrak{u}}(x,y)&=\inf\left\{\displaystyle\sum_{i=1}^{m}\mathfrak{u}(d^X(z_{i-1}, z_i))\,:\, z_0=x, z_1,\dots, z_m=y\in X\right\}. \end{align*} $$
$$ \begin{align*} d^X_{\mathfrak{u}}(x,y)&=\inf\left\{\displaystyle\sum_{i=1}^{m}\mathfrak{u}(d^X(z_{i-1}, z_i))\,:\, z_0=x, z_1,\dots, z_m=y\in X\right\}. \end{align*} $$
Definition 3.4. Let
![]() $(X, d^X)$
be a metric space and let
$(X, d^X)$
be a metric space and let
![]() $R\in \mathcal {L}$
be n-ary. Define
$R\in \mathcal {L}$
be n-ary. Define
 $$ \begin{align*}d^X_R(\overline{x}, \overline{y})=\displaystyle\sum_{i=1}^n d^X_{\mathfrak{u}_{R,i}}(x_i, y_i)\end{align*} $$
$$ \begin{align*}d^X_R(\overline{x}, \overline{y})=\displaystyle\sum_{i=1}^n d^X_{\mathfrak{u}_{R,i}}(x_i, y_i)\end{align*} $$
for
![]() $\overline {x}=(x_1,\dots , x_n), \overline {y}=(y_1,\dots , y_n)\in X^n$
.
$\overline {x}=(x_1,\dots , x_n), \overline {y}=(y_1,\dots , y_n)\in X^n$
.
For each n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $d^X_R$
is a pseudo-metric on
$d^X_R$
is a pseudo-metric on
![]() $X^n$
.
$X^n$
.
Lemma 3.5. Let
![]() $(M,d^M)$
be a metric space with
$(M,d^M)$
be a metric space with
![]() $R^M$
defined on
$R^M$
defined on
![]() $M^n$
for all n-ary
$M^n$
for all n-ary
![]() $R\in \mathcal {L}$
. Then
$R\in \mathcal {L}$
. Then
![]() $\mathcal {M}=(M, d^M, (R^M)_{R\in \mathcal {L}})$
is a continuous
$\mathcal {M}=(M, d^M, (R^M)_{R\in \mathcal {L}})$
is a continuous
![]() $\mathcal {L}$
-pre-structure, i.e., (
UC
ℒ
) holds for
$\mathcal {L}$
-pre-structure, i.e., (
UC
ℒ
) holds for
![]() $\mathcal {M}$
iff for any n-ary
$\mathcal {M}$
iff for any n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^M$
is
$R^M$
is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $d^M_R$
.
$d^M_R$
.
Proof Suppose
![]() $R\in \mathcal {L}$
is n-ary and
$R\in \mathcal {L}$
is n-ary and
![]() $R^M$
is
$R^M$
is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $d^M_R$
. Let
$d^M_R$
. Let
![]() $\overline {x}, \overline {y}\in M^n$
only differ at the ith coordinate. Then
$\overline {x}, \overline {y}\in M^n$
only differ at the ith coordinate. Then
Conversely, suppose (UCℒ
) holds for
![]() $\mathcal {M}$
for n-ary
$\mathcal {M}$
for n-ary
![]() $R\in \mathcal {L}$
. Let
$R\in \mathcal {L}$
. Let
![]() $\overline {x}, \overline {y}\in M^n$
. For
$\overline {x}, \overline {y}\in M^n$
. For
![]() $0\leq p\leq n$
, let
$0\leq p\leq n$
, let
For each
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $w_{i,0}=x_i, w_{i,1},\dots , w_{i,m_i}=y_i\in M$
be arbitrary and let
$w_{i,0}=x_i, w_{i,1},\dots , w_{i,m_i}=y_i\in M$
be arbitrary and let
for
![]() $0\leq j\leq m_i$
. Then
$0\leq j\leq m_i$
. Then
 $$ \begin{align*}|R^M(\overline{x})-R^M(\overline{y})|&\leq \displaystyle\sum_{i=1}^{n}|R^M(\overline{z}^{i-1})-R^M(\overline{z}^{i})| \\ &\leq \displaystyle\sum_{i=1}^n\sum_{j=1}^{m_i}|R^M(\overline{z}^{i,j-1})-R^M(\overline{z}^{i,j})| \\ &\leq \displaystyle\sum_{i=1}^n \sum_{j=1}^{m_i} \mathfrak{u}_{R,i}(d^M(w_{i,j-1}, w_j)). \end{align*} $$
$$ \begin{align*}|R^M(\overline{x})-R^M(\overline{y})|&\leq \displaystyle\sum_{i=1}^{n}|R^M(\overline{z}^{i-1})-R^M(\overline{z}^{i})| \\ &\leq \displaystyle\sum_{i=1}^n\sum_{j=1}^{m_i}|R^M(\overline{z}^{i,j-1})-R^M(\overline{z}^{i,j})| \\ &\leq \displaystyle\sum_{i=1}^n \sum_{j=1}^{m_i} \mathfrak{u}_{R,i}(d^M(w_{i,j-1}, w_j)). \end{align*} $$
Taking the infimum among all
![]() $w_{i,0}, \dots , w_{i,m_i}$
, we get
$w_{i,0}, \dots , w_{i,m_i}$
, we get
 $$ \begin{align*}|R^M(\overline{x})-R^M(\overline{y})|\leq \displaystyle\sum_{i=1}^n d^M_{\mathfrak{u}_{R,i}}(x_i,y_i)=d^M_R(\overline{x}, \overline{y}).\\[-41pt] \end{align*} $$
$$ \begin{align*}|R^M(\overline{x})-R^M(\overline{y})|\leq \displaystyle\sum_{i=1}^n d^M_{\mathfrak{u}_{R,i}}(x_i,y_i)=d^M_R(\overline{x}, \overline{y}).\\[-41pt] \end{align*} $$
Definition 3.6.
-
(i) A partially defined continuous
 $\mathcal {L}$
-pre-structure is a tuple where
$\mathcal {L}$
-pre-structure is a tuple where $$ \begin{align*}\mathcal{X}=(X, d^X, (R^X)_{R\in\mathcal{L}}),\end{align*} $$
$$ \begin{align*}\mathcal{X}=(X, d^X, (R^X)_{R\in\mathcal{L}}),\end{align*} $$
 $(X, d^X)$
is a metric space, and for each n-ary
$(X, d^X)$
is a metric space, and for each n-ary
 $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
 $R^X:{\mathrm {dom}}(R^X)\to [0,1]$
is a function with domain
$R^X:{\mathrm {dom}}(R^X)\to [0,1]$
is a function with domain
 ${\mathrm {dom}}(R^X)\subseteq X^n$
which is
${\mathrm {dom}}(R^X)\subseteq X^n$
which is
 $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
 $d^X_R$
.
$d^X_R$
.
-
(ii) Let
 $\mathcal {X}$
be a partially defined continuous
$\mathcal {X}$
be a partially defined continuous
 $\mathcal {L}$
-pre-structure. A continuous
$\mathcal {L}$
-pre-structure. A continuous
 $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
 $\mathcal {M}$
is a conservative extension of
$\mathcal {M}$
is a conservative extension of
 $\mathcal {X}$
if
$\mathcal {X}$
if
 $(M,d^M)=(X,d^X)$
and for any
$(M,d^M)=(X,d^X)$
and for any
 $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
 $R^M\,{\!\upharpoonright \!}\,\, {\mathrm {dom}}(R^X)=R^X$
.
$R^M\,{\!\upharpoonright \!}\,\, {\mathrm {dom}}(R^X)=R^X$
.
Lemma 3.7. Any partially defined continuous
![]() $\mathcal {L}$
-pre-structure has a conservative extension.
$\mathcal {L}$
-pre-structure has a conservative extension.
Proof Let
![]() $\mathcal {X}$
be a partially defined continuous
$\mathcal {X}$
be a partially defined continuous
![]() $\mathcal {L}$
-pre-structure. Define
$\mathcal {L}$
-pre-structure. Define
![]() $(M, d^M)=(X,d^X)$
and for any n-ary
$(M, d^M)=(X,d^X)$
and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {x}\in M^n$
, define
$\overline {x}\in M^n$
, define
It is clear that if
![]() $\overline {x}\in {\mathrm {dom}}(R^X)$
, then
$\overline {x}\in {\mathrm {dom}}(R^X)$
, then
![]() $R^M(\overline {x})=R^X(\overline {x})$
.
$R^M(\overline {x})=R^X(\overline {x})$
.
To complete the proof, it suffices to verify that
![]() $\mathcal {M}$
satisfies (UCℒ
). By Lemma 3.5 it suffices to show that for any n-ary
$\mathcal {M}$
satisfies (UCℒ
). By Lemma 3.5 it suffices to show that for any n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^M$
is
$R^M$
is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $d^M_R$
. Suppose
$d^M_R$
. Suppose
![]() $\overline {x}, \overline {y}\in M^n$
. Assume toward a contradiction that
$\overline {x}, \overline {y}\in M^n$
. Assume toward a contradiction that
![]() $R^M(\overline {x})-R^M(\overline {y})>d^M_R(\overline {x},\overline {y})$
. Let
$R^M(\overline {x})-R^M(\overline {y})>d^M_R(\overline {x},\overline {y})$
. Let
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
In particular
![]() $R^M(\overline {x})>0$
. By the definition of
$R^M(\overline {x})>0$
. By the definition of
![]() $R^M(\overline {x})$
there is
$R^M(\overline {x})$
there is
![]() $\overline {z}\in {\mathrm {dom}}(R^X)$
such that
$\overline {z}\in {\mathrm {dom}}(R^X)$
such that
Then
 $$ \begin{align*} R^X(\overline{z})-R^M(\overline{y})&= R^X(\overline{z})-R^M(\overline{x})+R^M(\overline{x})-R^M(\overline{y}) \\&> d^X_R(\overline{x},\overline{z})-\epsilon+ d^X_R(\overline{x},\overline{y})+\epsilon \\&\geq d^X_R(\overline{z},\overline{y}). \end{align*} $$
$$ \begin{align*} R^X(\overline{z})-R^M(\overline{y})&= R^X(\overline{z})-R^M(\overline{x})+R^M(\overline{x})-R^M(\overline{y}) \\&> d^X_R(\overline{x},\overline{z})-\epsilon+ d^X_R(\overline{x},\overline{y})+\epsilon \\&\geq d^X_R(\overline{z},\overline{y}). \end{align*} $$
Thus
![]() $R^X(\overline {z})- d^X_R(\overline {z},\overline {y})>R^M(\overline {y})$
, contradicting the definition of
$R^X(\overline {z})- d^X_R(\overline {z},\overline {y})>R^M(\overline {y})$
, contradicting the definition of
![]() $R^M(\overline {y})$
.
$R^M(\overline {y})$
.
We are now ready to prove the first characterization.
Theorem 3.8. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. The following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. The following are equivalent:
-
(1)
 $\mathcal {L}$
is semiproper.
$\mathcal {L}$
is semiproper. -
(2) The class of all finite continuous
 $\mathcal {L}$
-structures has the AP.
$\mathcal {L}$
-structures has the AP. -
(3) The class of all finite continuous
 $\mathcal {L}$
-structures has the SAP.
$\mathcal {L}$
-structures has the SAP.
Proof We prove the implications (1)
![]() $\Rightarrow $
(3) and (2)
$\Rightarrow $
(3) and (2)
![]() $\Rightarrow $
(1).
$\Rightarrow $
(1).
For (1)
![]() $\Rightarrow $
(3), let
$\Rightarrow $
(3), let
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {Q}$
be finite continuous
$\mathcal {Q}$
be finite continuous
![]() $\mathcal {L}$
-structures, and let
$\mathcal {L}$
-structures, and let
![]() $\varphi : \mathcal {M}\to \mathcal {P}$
and
$\varphi : \mathcal {M}\to \mathcal {P}$
and
![]() $\psi :\mathcal {M}\to \mathcal {Q}$
be isomorphic embeddings. To ease notation we regard
$\psi :\mathcal {M}\to \mathcal {Q}$
be isomorphic embeddings. To ease notation we regard
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
as identity maps. Let X be the disjoint union of M,
$\psi $
as identity maps. Let X be the disjoint union of M,
![]() $P\setminus M$
, and
$P\setminus M$
, and
![]() $Q\setminus M$
. Define a metric
$Q\setminus M$
. Define a metric
![]() $d^X$
on X by the obvious definitions except for
$d^X$
on X by the obvious definitions except for
![]() $x\in P\setminus M$
and
$x\in P\setminus M$
and
![]() $y\in Q\setminus M$
we set
$y\in Q\setminus M$
we set
For an n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^X$
is naturally defined on
$R^X$
is naturally defined on
![]() ${\mathrm {dom}}(R^X)= P^n \cup Q^n$
.
${\mathrm {dom}}(R^X)= P^n \cup Q^n$
.
We verify that
![]() $\mathcal {X}=(X,d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
$\mathcal {X}=(X,d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure. For this, fix an n-ary
$\mathcal {L}$
-pre-structure. For this, fix an n-ary
![]() $R\in \mathcal {L}$
and consider
$R\in \mathcal {L}$
and consider
![]() $\overline {x}=(x_1,\dots , x_n), \overline {y}=(y_1,\dots , y_n)\in {\mathrm {dom}}(R^X)$
.
$\overline {x}=(x_1,\dots , x_n), \overline {y}=(y_1,\dots , y_n)\in {\mathrm {dom}}(R^X)$
.
First suppose
![]() $n=1$
. In this case we claim that for any
$n=1$
. In this case we claim that for any
![]() $u, v\in P\cup Q$
,
$u, v\in P\cup Q$
,
From the claim it follows quickly that
To prove the claim, we only need to consider the situation where
![]() $u\in P\setminus M$
and
$u\in P\setminus M$
and
![]() $v\in Q\setminus M$
. Note that for any
$v\in Q\setminus M$
. Note that for any
![]() $z\in M$
,
$z\in M$
,
 $$ \begin{align*} |R^X(u)-R^X(v)|&\leq |R^X(u)-R^X(z)|+|R^X(z)-R^X(v)|\\ &=|R^P(u)-R^P(z)|+|R^Q(z)-R^Q(v)| \\ &\leq \mathfrak{u}_{R,1}(d^P(u, z))+\mathfrak{u}_{R,1}(d^Q(z,v)) \end{align*} $$
$$ \begin{align*} |R^X(u)-R^X(v)|&\leq |R^X(u)-R^X(z)|+|R^X(z)-R^X(v)|\\ &=|R^P(u)-R^P(z)|+|R^Q(z)-R^Q(v)| \\ &\leq \mathfrak{u}_{R,1}(d^P(u, z))+\mathfrak{u}_{R,1}(d^Q(z,v)) \end{align*} $$
by (UCℒ
) for
![]() $R^P$
and
$R^P$
and
![]() $R^Q$
. If
$R^Q$
. If
![]() $d^X(u,v)\not \in I_{R,1}$
, then we certainly have
$d^X(u,v)\not \in I_{R,1}$
, then we certainly have
Otherwise, we may consider only those
![]() $z\in M$
with
$z\in M$
with
![]() $d^P(u, z)+d^Q( z,v)\in I_{R,1}$
. By the superadditivity of
$d^P(u, z)+d^Q( z,v)\in I_{R,1}$
. By the superadditivity of
![]() $\mathfrak {u}_{R,1}$
on
$\mathfrak {u}_{R,1}$
on
![]() $I_{R,1}$
, we have
$I_{R,1}$
, we have
Taking the infimum over such
![]() $z\in M$
, and noting that M is finite, we have by the monotonicity of
$z\in M$
, and noting that M is finite, we have by the monotonicity of
![]() $\mathfrak {u}_{R,1}$
that
$\mathfrak {u}_{R,1}$
that
Next suppose
![]() $n\geq 2$
. In this case we have that for all
$n\geq 2$
. In this case we have that for all
![]() $1\leq i\leq n$
, there is some
$1\leq i\leq n$
, there is some
![]() $K_{R,i}>0$
such that
$K_{R,i}>0$
such that
![]() $\mathfrak {u}_{R,i}(r)=K_{R,i} r$
for all
$\mathfrak {u}_{R,i}(r)=K_{R,i} r$
for all
![]() $r\in I_{R,i}$
. It is easy to check that for any
$r\in I_{R,i}$
. It is easy to check that for any
![]() $u, v\in P$
,
$u, v\in P$
,
Similarly for
![]() $u, v\in Q$
. From these, the cases when
$u, v\in Q$
. From these, the cases when
![]() $\overline {x}, \overline {y}\in P^n$
and
$\overline {x}, \overline {y}\in P^n$
and
![]() $\overline {x}, \overline {y}\in Q^n$
quickly follow from Lemma 3.5.
$\overline {x}, \overline {y}\in Q^n$
quickly follow from Lemma 3.5.
Next we consider the case where
![]() $\overline {x}\in P^n$
and
$\overline {x}\in P^n$
and
![]() $\overline {y}\in Q^n$
. Define
$\overline {y}\in Q^n$
. Define
 $$ \begin{align*}S_0 & = \{ i\,:\, x_i, y_i\in M\}, \\ S_1 & = \{ i\,:\, x_i\in P\setminus M, y_i\in M\}, \\ S_2 & = \{ i\,:\, x_i\in M, y_i\in Q\setminus M\}, \\ S_3 & = \{ i \,:\, x_i\in P\setminus M, y_i\in Q\setminus M\}. \end{align*} $$
$$ \begin{align*}S_0 & = \{ i\,:\, x_i, y_i\in M\}, \\ S_1 & = \{ i\,:\, x_i\in P\setminus M, y_i\in M\}, \\ S_2 & = \{ i\,:\, x_i\in M, y_i\in Q\setminus M\}, \\ S_3 & = \{ i \,:\, x_i\in P\setminus M, y_i\in Q\setminus M\}. \end{align*} $$
Define
![]() $\overline {u}=(u_1,\dots , u_n), \overline {v}=(v_1,\dots , v_n)\in {\mathrm {dom}}(R^X)$
by
$\overline {u}=(u_1,\dots , u_n), \overline {v}=(v_1,\dots , v_n)\in {\mathrm {dom}}(R^X)$
by
 $$ \begin{align*}u_i=\left\{\begin{array}{@{}ll} x_i, & \mbox{ if}\ i\in S_2\cup S_3, \\ y_i, & \mbox{ if}\ i\in S_0\cup S_1, \end{array}\right.\end{align*} $$
$$ \begin{align*}u_i=\left\{\begin{array}{@{}ll} x_i, & \mbox{ if}\ i\in S_2\cup S_3, \\ y_i, & \mbox{ if}\ i\in S_0\cup S_1, \end{array}\right.\end{align*} $$
and
 $$ \begin{align*}v_i=\left\{\begin{array}{@{}ll} x_i, & \mbox{ if}\ i\in S_2, \\ y_i, & \mbox{ if}\ i\in S_0\cup S_1\cup S_3. \end{array}\right.\end{align*} $$
$$ \begin{align*}v_i=\left\{\begin{array}{@{}ll} x_i, & \mbox{ if}\ i\in S_2, \\ y_i, & \mbox{ if}\ i\in S_0\cup S_1\cup S_3. \end{array}\right.\end{align*} $$
Given any
![]() $\overline {z}\in M^n$
, by Lemma 3.5 we have
$\overline {z}\in M^n$
, by Lemma 3.5 we have
 $$ \begin{align*} |R^X(\overline{u})-R^X(\overline{v})| &\leq |R^X(\overline{u})-R^X(\overline{z})|+|R^X(\overline{z})-R^X(\overline{v})| \\ & \leq d^P_R(\overline{u},\overline{z})+d^Q_R(\overline{z},\overline{v}) \\ & = \displaystyle\sum_{i=1}^n d^P_{\mathfrak{u}_{R,i}}(u_i,z_i)+\sum_{i=1}^n d^Q_{\mathfrak{u}_{R,i}}(z_i,v_i) \\ &= \displaystyle\sum_{i=1}^n K_{R,i}(d^P(u_i, z_i)+d^Q(z_i, v_i)). \end{align*} $$
$$ \begin{align*} |R^X(\overline{u})-R^X(\overline{v})| &\leq |R^X(\overline{u})-R^X(\overline{z})|+|R^X(\overline{z})-R^X(\overline{v})| \\ & \leq d^P_R(\overline{u},\overline{z})+d^Q_R(\overline{z},\overline{v}) \\ & = \displaystyle\sum_{i=1}^n d^P_{\mathfrak{u}_{R,i}}(u_i,z_i)+\sum_{i=1}^n d^Q_{\mathfrak{u}_{R,i}}(z_i,v_i) \\ &= \displaystyle\sum_{i=1}^n K_{R,i}(d^P(u_i, z_i)+d^Q(z_i, v_i)). \end{align*} $$
Taking the infimum over all
![]() $\overline {z}\in M^n$
, we get that
$\overline {z}\in M^n$
, we get that
 $$ \begin{align*}|R^X(\overline{u})-R^X(\overline{v})|\leq \displaystyle\sum_{i=1}^n K_{R,i}d^X(u_i,v_i)=\sum_{i=1}^nd^X_{\mathfrak{u}_{R,i}}(u_i, v_i)= d^X_R(\overline{u},\overline{v}). \end{align*} $$
$$ \begin{align*}|R^X(\overline{u})-R^X(\overline{v})|\leq \displaystyle\sum_{i=1}^n K_{R,i}d^X(u_i,v_i)=\sum_{i=1}^nd^X_{\mathfrak{u}_{R,i}}(u_i, v_i)= d^X_R(\overline{u},\overline{v}). \end{align*} $$
Thus
 $$ \begin{align*}& |R^X(\overline{x})-R^X(\overline{y})|\\ & \quad \leq |R^X(\overline{x})-R^X(\overline{u})|+|R^X(\overline{u})-R^X(\overline{v})|+|R^X(\overline{v})-R^X(\overline{y})| \\& \quad \leq d_R^X(\overline{x},\overline{u})+d^X_R(\overline{u},\overline{v})+d^X_R(\overline{v},\overline{y}) \\& \quad \leq \displaystyle\sum_{i\in S_0\cup S_1} d^X_{\mathfrak{u}_{R,i}}(x_i, y_i) + \sum_{i\in S_3} d^X_{\mathfrak{u}_{R,i}}(x_i, y_i)+\sum_{i\in S_2} d^X_{\mathfrak{u}_{R,i}}(x_i,y_i) \\& \quad = d^X_R(\overline{x},\overline{y}). \end{align*} $$
$$ \begin{align*}& |R^X(\overline{x})-R^X(\overline{y})|\\ & \quad \leq |R^X(\overline{x})-R^X(\overline{u})|+|R^X(\overline{u})-R^X(\overline{v})|+|R^X(\overline{v})-R^X(\overline{y})| \\& \quad \leq d_R^X(\overline{x},\overline{u})+d^X_R(\overline{u},\overline{v})+d^X_R(\overline{v},\overline{y}) \\& \quad \leq \displaystyle\sum_{i\in S_0\cup S_1} d^X_{\mathfrak{u}_{R,i}}(x_i, y_i) + \sum_{i\in S_3} d^X_{\mathfrak{u}_{R,i}}(x_i, y_i)+\sum_{i\in S_2} d^X_{\mathfrak{u}_{R,i}}(x_i,y_i) \\& \quad = d^X_R(\overline{x},\overline{y}). \end{align*} $$
We have thus completed the verification that
![]() $\mathcal {X}$
is a partially defined continuous
$\mathcal {X}$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure. Applying Lemma 3.7 to
$\mathcal {L}$
-pre-structure. Applying Lemma 3.7 to
![]() $\mathcal {X}$
, we obtain a conservative extension
$\mathcal {X}$
, we obtain a conservative extension
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {X}$
. This
$\mathcal {X}$
. This
![]() $\mathcal {N}$
satisfies the requirements of the strong amalgamation property.
$\mathcal {N}$
satisfies the requirements of the strong amalgamation property.
(2)
![]() $\Rightarrow $
(1). Let
$\Rightarrow $
(1). Let
![]() $R\in \mathcal {L}$
be n-ary and
$R\in \mathcal {L}$
be n-ary and
![]() $1\leq i\leq n$
. We claim that
$1\leq i\leq n$
. We claim that
for all
![]() $r_1, r_2>0$
with
$r_1, r_2>0$
with
![]() $r_1+r_2\in I_{R,i}=\{r\,:\, \mathfrak {u}_{R,i}(r)< 1\}$
. To prove the claim, let
$r_1+r_2\in I_{R,i}=\{r\,:\, \mathfrak {u}_{R,i}(r)< 1\}$
. To prove the claim, let
![]() $r_1, r_2>0$
so that
$r_1, r_2>0$
so that
![]() $r_1+r_2\in I_{R,i}$
. Consider finite continuous
$r_1+r_2\in I_{R,i}$
. Consider finite continuous
![]() $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {Q}$
where for all
$\mathcal {Q}$
where for all
![]() $R'\in \mathcal {L}$
with
$R'\in \mathcal {L}$
with
![]() $R'\neq R$
, the values of
$R'\neq R$
, the values of
![]() ${R'}^M$
,
${R'}^M$
,
![]() ${R'}^P$
,
${R'}^P$
,
![]() ${R'}^Q$
are identically
${R'}^Q$
are identically
![]() $0$
, and
$0$
, and
-
•
 $M=\{x_0\}$
,
$M=\{x_0\}$
,
 $R^M(\overline {x})=\mathfrak {u}_{R,i}(r_1)$
where
$R^M(\overline {x})=\mathfrak {u}_{R,i}(r_1)$
where
 $\overline {x}=(x_0,\dots , x_0)\in M^n$
;
$\overline {x}=(x_0,\dots , x_0)\in M^n$
; -
•
 $P= \{ x_0, x_1\}$
,
$P= \{ x_0, x_1\}$
,
 $d^P(x_0, x_1)=r_1$
, and for all
$d^P(x_0, x_1)=r_1$
, and for all
 $\overline {y}=(y_1, \dots , y_n)\in P^n$
,
$\overline {y}=(y_1, \dots , y_n)\in P^n$
,  $$ \begin{align*}R^P(\overline{y})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R, i}(r_1), & \mbox{ if}\ y_i=x_0, \\ 0, & \mbox{otherwise;} \end{array}\right.\end{align*} $$
$$ \begin{align*}R^P(\overline{y})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R, i}(r_1), & \mbox{ if}\ y_i=x_0, \\ 0, & \mbox{otherwise;} \end{array}\right.\end{align*} $$
-
•
 $Q=\{x_0, x_2\}$
,
$Q=\{x_0, x_2\}$
,
 $d^Q(x_0,x_2)=r_2$
, and for all
$d^Q(x_0,x_2)=r_2$
, and for all
 $\overline {y}=(y_1, \dots , y_n)\in Q^n$
,
$\overline {y}=(y_1, \dots , y_n)\in Q^n$
,  $$ \begin{align*}R^Q(\overline{y})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R, i}(r_1), & \mbox{ if}\ y_i=x_0, \\ \min\{1, \mathfrak{u}_{R, i}(r_1)+\mathfrak{u}_{R, i}(r_2)\}, & \mbox{otherwise.} \end{array}\right.\end{align*} $$
$$ \begin{align*}R^Q(\overline{y})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R, i}(r_1), & \mbox{ if}\ y_i=x_0, \\ \min\{1, \mathfrak{u}_{R, i}(r_1)+\mathfrak{u}_{R, i}(r_2)\}, & \mbox{otherwise.} \end{array}\right.\end{align*} $$
Let
![]() $\mathcal {N}$
be an amalgam of
$\mathcal {N}$
be an amalgam of
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $\overline {x}'$
be obtained from
$\overline {x}'$
be obtained from
![]() $\overline {x}$
by replacing the ith coordinate of
$\overline {x}$
by replacing the ith coordinate of
![]() $\overline {x}$
by
$\overline {x}$
by
![]() $x_1$
, and similarly
$x_1$
, and similarly
![]() $\overline {x}"$
be obtained from
$\overline {x}"$
be obtained from
![]() $\overline {x}$
by replacing the ith coordinate of
$\overline {x}$
by replacing the ith coordinate of
![]() $\overline {x}$
by
$\overline {x}$
by
![]() $x_2$
. Then by the monotonicity of
$x_2$
. Then by the monotonicity of
![]() $\mathfrak {u}_{R,i}$
, we have
$\mathfrak {u}_{R,i}$
, we have
 $$ \begin{align*} \mbox{min}\{1, \mathfrak{u}_{R,i}(r_1)+\mathfrak{u}_{R,i}(r_2)\}&=|R^N(\overline{x}')-R^N(\overline{x}")| \\&\leq \mathfrak{u}_{R,i}(d^N(x_1, x_2)) \\&\leq \mathfrak{u}_{R,i}(d^P(x_1,x_0)+d^Q(x_0,x_2))=\mathfrak{u}_{R,i}(r_1+r_2). \end{align*} $$
$$ \begin{align*} \mbox{min}\{1, \mathfrak{u}_{R,i}(r_1)+\mathfrak{u}_{R,i}(r_2)\}&=|R^N(\overline{x}')-R^N(\overline{x}")| \\&\leq \mathfrak{u}_{R,i}(d^N(x_1, x_2)) \\&\leq \mathfrak{u}_{R,i}(d^P(x_1,x_0)+d^Q(x_0,x_2))=\mathfrak{u}_{R,i}(r_1+r_2). \end{align*} $$
Since
![]() $\mathfrak {u}_{R,i}(r_1+r_2)<1$
, we have
$\mathfrak {u}_{R,i}(r_1+r_2)<1$
, we have
![]() $\mathfrak {u}_{R,i}(r_1)+\mathfrak {u}_{R,i}(r_2)\leq \mathfrak {u}_{R,i}(r_1+r_2)$
as desired.
$\mathfrak {u}_{R,i}(r_1)+\mathfrak {u}_{R,i}(r_2)\leq \mathfrak {u}_{R,i}(r_1+r_2)$
as desired.
It follows that
![]() $I_{R,i}$
is bounded. In fact, if
$I_{R,i}$
is bounded. In fact, if
![]() $I_{R,i}$
were unbounded then
$I_{R,i}$
were unbounded then
![]() $I_{R,i}=[0,+\infty )$
and
$I_{R,i}=[0,+\infty )$
and
![]() $M=\sup \{\, \mathfrak {u}_{R,i}(r)\,:\, r\geq 0\}\leq 1$
. Let
$M=\sup \{\, \mathfrak {u}_{R,i}(r)\,:\, r\geq 0\}\leq 1$
. Let
![]() $r_1, r_2>0$
be such that
$r_1, r_2>0$
be such that
![]() $\mathfrak {u}_{R,i}(r_1),\mathfrak {u}_{R,i}(r_2)>M/2$
. Then
$\mathfrak {u}_{R,i}(r_1),\mathfrak {u}_{R,i}(r_2)>M/2$
. Then
![]() $\mathfrak {u}_{R,i}(r_1+r_2)>M$
, contradicting the definition of M.
$\mathfrak {u}_{R,i}(r_1+r_2)>M$
, contradicting the definition of M.
For the rest of the semiproperness of
![]() $\mathcal {L}$
, suppose
$\mathcal {L}$
, suppose
![]() $n\geq 2$
. Without loss of generality consider
$n\geq 2$
. Without loss of generality consider
![]() $i=1$
. The proof for
$i=1$
. The proof for
![]() $1<i\leq n$
is similar. Let
$1<i\leq n$
is similar. Let
![]() $r_1, r_2$
be such that
$r_1, r_2$
be such that
![]() ${r_1+r_2\in I_{R,i}}$
. Let
${r_1+r_2\in I_{R,i}}$
. Let
![]() $r>r_1+r_2$
be an upper bound for
$r>r_1+r_2$
be an upper bound for
![]() $I_{R,n}$
. Consider finite continuous
$I_{R,n}$
. Consider finite continuous
![]() $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {Q}$
where for all
$\mathcal {Q}$
where for all
![]() $R'\in \mathcal {L}$
with
$R'\in \mathcal {L}$
with
![]() $R'\neq R$
, the values of
$R'\neq R$
, the values of
![]() ${R'}^M$
,
${R'}^M$
,
![]() ${R'}^P$
,
${R'}^P$
,
![]() ${R'}^Q$
are identically
${R'}^Q$
are identically
![]() $0$
, and
$0$
, and
-
•
 $M=\{x_0, u_0\}$
,
$M=\{x_0, u_0\}$
,
 $d^M(x_0, u_0)=r_1+r_2$
,
$d^M(x_0, u_0)=r_1+r_2$
,
 $R^M(\overline {x})=0$
for all
$R^M(\overline {x})=0$
for all
 $\overline {x}\in M^n$
;
$\overline {x}\in M^n$
; -
•
 $P= \{ x_0, u_0, x_1\}$
,
$P= \{ x_0, u_0, x_1\}$
,
 $d^P(x_0, x_1)=d^P(u_0, x_1)=r>r_1+r_2$
,
$d^P(x_0, x_1)=d^P(u_0, x_1)=r>r_1+r_2$
,  $$ \begin{align*}R^P(\overline{y})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R,1}(r_1+r_2), & \mbox{ if}\ y_1=x_0 \mbox{ and}\ y_n=x_1, \\ 0, & \mbox{ otherwise;} \end{array}\right.\end{align*} $$
$$ \begin{align*}R^P(\overline{y})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R,1}(r_1+r_2), & \mbox{ if}\ y_1=x_0 \mbox{ and}\ y_n=x_1, \\ 0, & \mbox{ otherwise;} \end{array}\right.\end{align*} $$
-
•
 $Q=\{x_0, u_0, x_2\}$
,
$Q=\{x_0, u_0, x_2\}$
,
 $d^Q(x_0,x_2)=r_1$
,
$d^Q(x_0,x_2)=r_1$
,
 $d^Q(u_0, x_2)=r_2$
,
$d^Q(u_0, x_2)=r_2$
,
 $R^Q(\overline {z})=0$
for all
$R^Q(\overline {z})=0$
for all
 $\overline {z}\in Q^n$
.
$\overline {z}\in Q^n$
.
Let
![]() $\mathcal {N}$
be an amalgam of
$\mathcal {N}$
be an amalgam of
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
 $$ \begin{align*}\overline{y}&= (x_0, x_0, \dots, x_0, x_1)\in P, \\ \overline{y}'&= (u_0, x_0, \dots, x_0, x_1)\in P, \\ \overline{w}&= (x_2, x_0, \dots, x_0, x_1)\in N. \end{align*} $$
$$ \begin{align*}\overline{y}&= (x_0, x_0, \dots, x_0, x_1)\in P, \\ \overline{y}'&= (u_0, x_0, \dots, x_0, x_1)\in P, \\ \overline{w}&= (x_2, x_0, \dots, x_0, x_1)\in N. \end{align*} $$
Then
 $$ \begin{align*}\mathfrak{u}_{R,1}(r_1+r_2)&= |R^N(\overline{y})-R^N(\overline{y}')| \\ &\leq |R^N(\overline{y})-R^N(\overline{w})|+|R^N(\overline{w})-R^N(\overline{y}')| \\ &\leq \mathfrak{u}_{R,1}(d^N(x_0, x_2))+\mathfrak{u}_{R,1}(d^N(u_0, x_2)) \\ &= \mathfrak{u}_{R,1}(r_1)+\mathfrak{u}_{R,1}(r_2). \end{align*} $$
$$ \begin{align*}\mathfrak{u}_{R,1}(r_1+r_2)&= |R^N(\overline{y})-R^N(\overline{y}')| \\ &\leq |R^N(\overline{y})-R^N(\overline{w})|+|R^N(\overline{w})-R^N(\overline{y}')| \\ &\leq \mathfrak{u}_{R,1}(d^N(x_0, x_2))+\mathfrak{u}_{R,1}(d^N(u_0, x_2)) \\ &= \mathfrak{u}_{R,1}(r_1)+\mathfrak{u}_{R,1}(r_2). \end{align*} $$
Thus we actually have
![]() $\mathfrak {u}_{R,1}(r_1+r_2)=\mathfrak {u}_{R,1}(r_1)+\mathfrak {u}_{R,1}(r_2)$
for all
$\mathfrak {u}_{R,1}(r_1+r_2)=\mathfrak {u}_{R,1}(r_1)+\mathfrak {u}_{R,1}(r_2)$
for all
![]() $r_1+r_2\in I_{R,1}$
. This implies that there is
$r_1+r_2\in I_{R,1}$
. This implies that there is
![]() $K_1>0$
such that
$K_1>0$
such that
![]() $\mathfrak {u}_{R,1}(r)=K_1r$
for all
$\mathfrak {u}_{R,1}(r)=K_1r$
for all
![]() $r\in I_{R,1}$
.
$r\in I_{R,1}$
.
Theorem 3.9. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. The following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. The following are equivalent:
-
(1)
 $\mathcal {L}$
is proper.
$\mathcal {L}$
is proper. -
(2) The class of all countable continuous
 $\mathcal {L}$
-pre-structures has the AP.
$\mathcal {L}$
-pre-structures has the AP. -
(3) The class of all countable continuous
 $\mathcal {L}$
-pre-structures has the SAP.
$\mathcal {L}$
-pre-structures has the SAP. -
(4) The class of all continuous
 $\mathcal {L}$
-pre-structures has the AP.
$\mathcal {L}$
-pre-structures has the AP. -
(5) The class of all continuous
 $\mathcal {L}$
-pre-structures has the SAP.
$\mathcal {L}$
-pre-structures has the SAP.
Proof The proof of (1)
![]() $\Rightarrow $
(3) follows exactly the same proof of (1)
$\Rightarrow $
(3) follows exactly the same proof of (1)
![]() $\Rightarrow $
(3) of Theorem 3.8, except in the last step of the verification of the
$\Rightarrow $
(3) of Theorem 3.8, except in the last step of the verification of the
![]() $1$
-Lipschitz property for the unary relation symbol, instead of using the finiteness of M we use the upper semicontinuity of
$1$
-Lipschitz property for the unary relation symbol, instead of using the finiteness of M we use the upper semicontinuity of
![]() $\mathfrak {u}_{R,1}$
. The proof of (1)
$\mathfrak {u}_{R,1}$
. The proof of (1)
![]() $\Rightarrow $
(5) is identical.
$\Rightarrow $
(5) is identical.
Conversely, for (2)
![]() $\Rightarrow $
(1) or (4)
$\Rightarrow $
(1) or (4)
![]() $\Rightarrow $
(1), we make the following observation. If
$\Rightarrow $
(1), we make the following observation. If
![]() $R\in \mathcal {L}$
is unary and not upper semicontinuous at
$R\in \mathcal {L}$
is unary and not upper semicontinuous at
![]() $r_0\in I_{R,1}$
, then choose some
$r_0\in I_{R,1}$
, then choose some
![]() $t_0\in (0,1)$
such that
$t_0\in (0,1)$
such that
Consider countable continuous
![]() $\mathcal {L}$
-pre-structures
$\mathcal {L}$
-pre-structures
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {Q}$
where for all
$\mathcal {Q}$
where for all
![]() $R'\in \mathcal {L}$
with
$R'\in \mathcal {L}$
with
![]() $R'\neq R$
, the values of
$R'\neq R$
, the values of
![]() ${R'}^M$
,
${R'}^M$
,
![]() ${R'}^P$
,
${R'}^P$
,
![]() ${R'}^Q$
are identically
${R'}^Q$
are identically
![]() $0$
, and
$0$
, and
-
•
 $M=\{x_i\,:\, i\geq 1\}$
,
$M=\{x_i\,:\, i\geq 1\}$
,
 $d^M(x_i, x_j)=|2^{-i}-2^{-j}|$
, for all
$d^M(x_i, x_j)=|2^{-i}-2^{-j}|$
, for all
 $i, j\geq 1$
, and
$i, j\geq 1$
, and
 $R^M(x_0)=0$
for all
$R^M(x_0)=0$
for all
 $i\geq 1$
;
$i\geq 1$
; -
•
 $P= M\cup \{x_0\}$
,
$P= M\cup \{x_0\}$
,
 $d^P(x_0, x_i)=r_0+2^{-i}$
,
$d^P(x_0, x_i)=r_0+2^{-i}$
,
 $R^P(x_0)=t_0$
;
$R^P(x_0)=t_0$
; -
•
 $Q=M\cup \{y_0\}$
,
$Q=M\cup \{y_0\}$
,
 $d^Q(y_0,x_i)=2^{-i}$
,
$d^Q(y_0,x_i)=2^{-i}$
,
 $R^Q(y_0)=0$
.
$R^Q(y_0)=0$
.
Let
![]() $\mathcal {N}$
be an amalgam of
$\mathcal {N}$
be an amalgam of
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $\mathcal {M}$
. Then
$\mathcal {M}$
. Then
 $$ \begin{align*} r_0=|d^N(x_0, x_i)-d^N(y_0, x_i)|&\leq d^N(x_0,y_0) \\ &\leq d^N(x_0, x_i)+d^N(y_0,x_i)=r_0+2^{-i+1} \end{align*} $$
$$ \begin{align*} r_0=|d^N(x_0, x_i)-d^N(y_0, x_i)|&\leq d^N(x_0,y_0) \\ &\leq d^N(x_0, x_i)+d^N(y_0,x_i)=r_0+2^{-i+1} \end{align*} $$
for all
![]() $i\geq 1$
. Letting
$i\geq 1$
. Letting
![]() $i\to \infty $
, we get
$i\to \infty $
, we get
![]() $d^N(x_0,y_0)=r_0$
. Now
$d^N(x_0,y_0)=r_0$
. Now
a contradiction.
Finally we give a characterization the AP and the SAP for the class of all (countable)
![]() $\mathcal {L}$
-structures. For this we need to introduce the following notion of strong semiproperness.
$\mathcal {L}$
-structures. For this we need to introduce the following notion of strong semiproperness.
Definition 3.10. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. We say that
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. We say that
![]() $\mathcal {L}$
is strongly semiproper if
$\mathcal {L}$
is strongly semiproper if
![]() $\mathcal {L}$
is semiproper and for any unary
$\mathcal {L}$
is semiproper and for any unary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $r_1, r_2>0$
with
$r_1, r_2>0$
with
![]() $r_1+r_2\in I_{R,1}$
,
$r_1+r_2\in I_{R,1}$
,
It is obvious that strong semiproperness implies semiproperness, and it is easy to see that properness implies strong semiproperness.
Theorem 3.11. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. The following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing. The following are equivalent:
-
(1)
 $\mathcal {L}$
is strongly semiproper.
$\mathcal {L}$
is strongly semiproper. -
(2) The class of all countable continuous
 $\mathcal {L}$
-structures has the AP.
$\mathcal {L}$
-structures has the AP. -
(3) The class of all countable continuous
 $\mathcal {L}$
-structures has the SAP.
$\mathcal {L}$
-structures has the SAP. -
(4) The class of all continuous
 $\mathcal {L}$
-structures has the AP.
$\mathcal {L}$
-structures has the AP. -
(5) The class of all continuous
 $\mathcal {L}$
-structures has the SAP.
$\mathcal {L}$
-structures has the SAP.
Proof The proof of (1)
![]() $\Rightarrow $
(3) again follows exactly the same proof of (1)
$\Rightarrow $
(3) again follows exactly the same proof of (1)
![]() $\Rightarrow $
(3) of Theorem 3.8, except that we need to modify the argument in the last step of the verification of the
$\Rightarrow $
(3) of Theorem 3.8, except that we need to modify the argument in the last step of the verification of the
![]() $1$
-Lipschitz property for the unary relation symbol. First we note that the metric space
$1$
-Lipschitz property for the unary relation symbol. First we note that the metric space
![]() $(X,d^X)$
is complete if both
$(X,d^X)$
is complete if both
![]() $(P,d^P)$
and
$(P,d^P)$
and
![]() $(Q,d^Q)$
are complete, and countable if both P and Q are countable. Let
$(Q,d^Q)$
are complete, and countable if both P and Q are countable. Let
![]() $R\in \mathcal {L}$
be unary,
$R\in \mathcal {L}$
be unary,
![]() $u\in P\setminus M$
and
$u\in P\setminus M$
and
![]() $v\in Q\setminus M$
. Then
$v\in Q\setminus M$
. Then
We may choose
![]() $\{z_n\}\subseteq M$
such that
$\{z_n\}\subseteq M$
such that
and both
![]() $\{d^P(u, z_n)\}_n$
and
$\{d^P(u, z_n)\}_n$
and
![]() $\{d^Q(z_n, v)\}_n$
are monotone. Let
$\{d^Q(z_n, v)\}_n$
are monotone. Let
If
![]() $r_1+r_2\not \in I_{R,1}$
then we have
$r_1+r_2\not \in I_{R,1}$
then we have
Suppose
![]() $r_1+r_2\in I_{R,1}$
. Then
$r_1+r_2\in I_{R,1}$
. Then
 $$ \begin{align*}|R^X(u)-R^X(v)|&\leq \inf\{ \mathfrak{u}_{R,1}(d^P(u,z))+\mathfrak{u}_{R,1}(d^Q(z, v))\,:\, z\in M\} \\&\leq \lim_n \left(\mathfrak{u}_{R,1}(d^P(u,z_n))+\mathfrak{u}_{R,1}(d^Q(z_n, v))\right)\\&\leq \inf\{\mathfrak{u}_{R,1}(r)\,:\, r>r_1\}+\inf\{\mathfrak{u}_{R,1}(r)\,:\, r>r_2\} \\&\leq \mathfrak{u}_{R,1}(r_1+r_2)=\mathfrak{u}_{R,1}(d^X(u,v)). \end{align*} $$
$$ \begin{align*}|R^X(u)-R^X(v)|&\leq \inf\{ \mathfrak{u}_{R,1}(d^P(u,z))+\mathfrak{u}_{R,1}(d^Q(z, v))\,:\, z\in M\} \\&\leq \lim_n \left(\mathfrak{u}_{R,1}(d^P(u,z_n))+\mathfrak{u}_{R,1}(d^Q(z_n, v))\right)\\&\leq \inf\{\mathfrak{u}_{R,1}(r)\,:\, r>r_1\}+\inf\{\mathfrak{u}_{R,1}(r)\,:\, r>r_2\} \\&\leq \mathfrak{u}_{R,1}(r_1+r_2)=\mathfrak{u}_{R,1}(d^X(u,v)). \end{align*} $$
The proof of (1)
![]() $\Rightarrow $
(5) is identical.
$\Rightarrow $
(5) is identical.
Conversely, we prove (2)
![]() $\Rightarrow $
(1) and (4)
$\Rightarrow $
(1) and (4)
![]() $\Rightarrow $
(1). By the proof of (2)
$\Rightarrow $
(1). By the proof of (2)
![]() $\Rightarrow $
(1) of Theorem 3.8,
$\Rightarrow $
(1) of Theorem 3.8,
![]() $\mathcal {L}$
is semiproper. To see that
$\mathcal {L}$
is semiproper. To see that
![]() $\mathcal {L}$
is strongly semiproper, let
$\mathcal {L}$
is strongly semiproper, let
![]() $R\in \mathcal {L}$
be unary and let
$R\in \mathcal {L}$
be unary and let
![]() $r_1, r_2>0$
be such that
$r_1, r_2>0$
be such that
![]() $r_1+r_2\in I_{R,1}$
. Without loss of generality assume
$r_1+r_2\in I_{R,1}$
. Without loss of generality assume
![]() $r_1\leq r_2$
. Let
$r_1\leq r_2$
. Let
![]() $M=\{x_n\,:\, n\in \mathbb {N}\}$
be a countably infinite set and define
$M=\{x_n\,:\, n\in \mathbb {N}\}$
be a countably infinite set and define
![]() $d^M(x_n,x_m)=r_1$
for all distinct
$d^M(x_n,x_m)=r_1$
for all distinct
![]() $n,m\in \mathbb {N}$
. Define
$n,m\in \mathbb {N}$
. Define
![]() $R^M(x)=\inf \{\mathfrak {u}_{R,1}(r)\,:\,r>r_1\}$
for all
$R^M(x)=\inf \{\mathfrak {u}_{R,1}(r)\,:\,r>r_1\}$
for all
![]() $x\in M$
and for any other
$x\in M$
and for any other
![]() $\tilde {R}\in \mathcal {L}$
, let
$\tilde {R}\in \mathcal {L}$
, let
![]() $\tilde {R}^M$
be identically
$\tilde {R}^M$
be identically
![]() $0$
. This defines a countable continuous
$0$
. This defines a countable continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $P=M\cup \{y\}$
where y is a fresh point. Define
$P=M\cup \{y\}$
where y is a fresh point. Define
![]() $d^P(x_n,y)=(1+2^{-n})r_1$
for all
$d^P(x_n,y)=(1+2^{-n})r_1$
for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $R^P(y)=0$
. For
$R^P(y)=0$
. For
![]() $\tilde {R}\in \mathcal {L}$
, let
$\tilde {R}\in \mathcal {L}$
, let
![]() $\tilde {R}^P$
be identically
$\tilde {R}^P$
be identically
![]() $0$
. This defines a countable continuous
$0$
. This defines a countable continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {P}$
that is an extension of
$\mathcal {P}$
that is an extension of
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $Q=M\cup \{z\}$
where z is a fresh point. Define
$Q=M\cup \{z\}$
where z is a fresh point. Define
![]() $d^Q(x_n, z)=r_2+2^{-n}r_1$
and
$d^Q(x_n, z)=r_2+2^{-n}r_1$
and
For
![]() $\tilde {R}\in \mathcal {L}$
, let
$\tilde {R}\in \mathcal {L}$
, let
![]() $\tilde {R}^Q$
be identically
$\tilde {R}^Q$
be identically
![]() $0$
. This defines a countable continuous
$0$
. This defines a countable continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {Q}$
that is an extension of
$\mathcal {Q}$
that is an extension of
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $\mathcal {N}$
be an amalgam of
$\mathcal {N}$
be an amalgam of
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $\mathcal {M}$
. Then for any
$\mathcal {M}$
. Then for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
Since n is arbitrary, we have
![]() $d^N(y,z)\leq r_1+r_2$
. Then
$d^N(y,z)\leq r_1+r_2$
. Then
 $$ \begin{align*}& \mbox{min}\left\{1, \inf\{ \mathfrak{u}_{R,1}(r)\,:\, r>r_1\}+\inf\{\mathfrak{u}_{R,1}(r)\,:\, r>r_2\}\right\} \\& \quad =|R^Q(z)-R^P(y)|=|R^N(z)-R^N(y)|\\& \quad = \mathfrak{u}_{R,1}(d^N(y,z))\leq \mathfrak{u}_{R,1}(r_1+r_2). \end{align*} $$
$$ \begin{align*}& \mbox{min}\left\{1, \inf\{ \mathfrak{u}_{R,1}(r)\,:\, r>r_1\}+\inf\{\mathfrak{u}_{R,1}(r)\,:\, r>r_2\}\right\} \\& \quad =|R^Q(z)-R^P(y)|=|R^N(z)-R^N(y)|\\& \quad = \mathfrak{u}_{R,1}(d^N(y,z))\leq \mathfrak{u}_{R,1}(r_1+r_2). \end{align*} $$
This shows that
![]() $\mathcal {L}$
is strongly semiproper.
$\mathcal {L}$
is strongly semiproper.
4. Urysohn continuous structures
In this section we give a Katětov-style construction of a Urysohn continuous
![]() $\mathcal {L}$
-structure for any proper continuous signature
$\mathcal {L}$
-structure for any proper continuous signature
![]() $\mathcal {L}$
. This will not only establish the usual properties of the Urysohn structure such as universality, ultrahomogeneity, and uniqueness, but also prove that its automorphism group is a universal Polish group.
$\mathcal {L}$
. This will not only establish the usual properties of the Urysohn structure such as universality, ultrahomogeneity, and uniqueness, but also prove that its automorphism group is a universal Polish group.
Throughout this section we assume that
![]() $\mathcal {L}$
is a proper continuous signature unless explicitly stated otherwise. For each unary
$\mathcal {L}$
is a proper continuous signature unless explicitly stated otherwise. For each unary
![]() $R\in \mathcal {L}$
, the modulus of continuity
$R\in \mathcal {L}$
, the modulus of continuity
![]() $\mathfrak {u}_{R,1}$
is nondecreasing, superadditive, and upper semicontinuous on
$\mathfrak {u}_{R,1}$
is nondecreasing, superadditive, and upper semicontinuous on
![]() $I_{R,1}$
. As in Lemma 2.3, we define
$I_{R,1}$
. As in Lemma 2.3, we define
![]() $\mathfrak {u}_{R,1}^*: [0,1)\to I_{R,1}$
, which is in particular subadditive on
$\mathfrak {u}_{R,1}^*: [0,1)\to I_{R,1}$
, which is in particular subadditive on
![]() $[0,1)$
. For n-ary
$[0,1)$
. For n-ary
![]() $R\in \mathcal {L}$
where
$R\in \mathcal {L}$
where
![]() $n\geq 2$
, we fix
$n\geq 2$
, we fix
![]() $K_{R,i}>0$
for
$K_{R,i}>0$
for
![]() $1\leq i\leq n$
so that
$1\leq i\leq n$
so that
![]() $\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
$\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
![]() $r\in I_{R,i}$
.
$r\in I_{R,i}$
.
Definition 4.1. Let
![]() $\mathcal {L}$
be a proper continuous signature,
$\mathcal {L}$
be a proper continuous signature,
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $\mathcal {U}$
be continuous
$\mathcal {U}$
be continuous
![]() $\mathcal {L}$
-pre-structures, and
$\mathcal {L}$
-pre-structures, and
![]() $\mathcal {K}$
a class of continuous
$\mathcal {K}$
a class of continuous
![]() $\mathcal {L}$
-pre-structures.
$\mathcal {L}$
-pre-structures.
-
(i)
 $\mathcal {N}$
is a one-point extension of
$\mathcal {N}$
is a one-point extension of
 $\mathcal {M}$
if
$\mathcal {M}$
if
 $\mathcal {M}$
is a substructure of
$\mathcal {M}$
is a substructure of
 $\mathcal {N}$
and
$\mathcal {N}$
and
 $N\setminus M$
is a singleton.
$N\setminus M$
is a singleton. -
(ii)
 $\mathcal {U}$
has the Urysohn property if given any finite continuous
$\mathcal {U}$
has the Urysohn property if given any finite continuous
 $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
 $\mathcal {M}$
, a one-point extension
$\mathcal {M}$
, a one-point extension
 $\mathcal {N}$
of
$\mathcal {N}$
of
 $\mathcal {M}$
, and an isomorphic embedding
$\mathcal {M}$
, and an isomorphic embedding
 $\varphi $
from
$\varphi $
from
 $\mathcal {M}$
into
$\mathcal {M}$
into
 $\mathcal {U}$
, there is an isomorphic embedding
$\mathcal {U}$
, there is an isomorphic embedding
 $\psi $
from
$\psi $
from
 $\mathcal {N}$
into
$\mathcal {N}$
into
 $\mathcal {U}$
such that
$\mathcal {U}$
such that
 $\psi \!\upharpoonright \! M=\varphi $
. We say
$\psi \!\upharpoonright \! M=\varphi $
. We say
 $\mathcal {U}$
is Urysohn if it satisfies the Urysohn property.
$\mathcal {U}$
is Urysohn if it satisfies the Urysohn property. -
(iii)
 $\mathcal {U}$
is universal for
$\mathcal {U}$
is universal for
 $\mathcal {K}$
if for any
$\mathcal {K}$
if for any
 $\mathcal {M}\in \mathcal {K}$
there is an isomorphic embedding from
$\mathcal {M}\in \mathcal {K}$
there is an isomorphic embedding from
 $\mathcal {M}$
into
$\mathcal {M}$
into
 $\mathcal {U}$
.
$\mathcal {U}$
. -
(iv)
 $\mathcal {U}$
is ultrahomogeneous if for any finite substructures
$\mathcal {U}$
is ultrahomogeneous if for any finite substructures
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $\mathcal {N}$
of
$\mathcal {N}$
of
 $\mathcal {U}$
and an isomorphism
$\mathcal {U}$
and an isomorphism
 $\varphi $
between
$\varphi $
between
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $\mathcal {N}$
, there is an automorphism
$\mathcal {N}$
, there is an automorphism
 $\psi $
of
$\psi $
of
 $\mathcal {U}$
such that
$\mathcal {U}$
such that
 $\psi \,{\!\upharpoonright \!}\,\, M=\varphi $
.
$\psi \,{\!\upharpoonright \!}\,\, M=\varphi $
.
Given a proper continuous signature
![]() $\mathcal {L}$
, let
$\mathcal {L}$
, let
and
By a standard argument, a separable continuous
![]() $\mathcal {L}$
-structure has the Urysohn property iff it is ultrahomogeneous and universal for
$\mathcal {L}$
-structure has the Urysohn property iff it is ultrahomogeneous and universal for
![]() ${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
. In this case, it is in fact universal for
${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
. In this case, it is in fact universal for
![]() ${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize sep}}}$
and unique up to isomorphism.
${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize sep}}}$
and unique up to isomorphism.
By Theorem 3.9, the class of all continuous
![]() $\mathcal {L}$
-pre-structures has the SAP. We call the continuous
$\mathcal {L}$
-pre-structures has the SAP. We call the continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {N}$
constructed in the proof of Theorem 3.9 the canonical amalgam of
$\mathcal {N}$
constructed in the proof of Theorem 3.9 the canonical amalgam of
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Definition 4.2. Let
![]() $\mathcal {M}, \mathcal {N}$
be continuous
$\mathcal {M}, \mathcal {N}$
be continuous
![]() $\mathcal {L}$
-pre-structures such that
$\mathcal {L}$
-pre-structures such that
![]() $\mathcal {M}$
is a substructure of
$\mathcal {M}$
is a substructure of
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
![]() $\mathcal {N}$
is said to be a finitely supported extension of
$\mathcal {N}$
is said to be a finitely supported extension of
![]() $\mathcal {M}$
if there is a finite subset
$\mathcal {M}$
if there is a finite subset
![]() $F\subseteq M$
such that, letting
$F\subseteq M$
such that, letting
![]() $\mathcal {F}$
be the substructure of
$\mathcal {F}$
be the substructure of
![]() $\mathcal {M}$
with domain F and
$\mathcal {M}$
with domain F and
![]() $\mathcal {A}$
be the substructure of
$\mathcal {A}$
be the substructure of
![]() $\mathcal {N}$
with domain
$\mathcal {N}$
with domain
![]() $A=F\cup (N\setminus M)$
,
$A=F\cup (N\setminus M)$
,
![]() $\mathcal {N}$
is the canonical amalgam of
$\mathcal {N}$
is the canonical amalgam of
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {M}$
over
$\mathcal {M}$
over
![]() $\mathcal {F}$
. In this case the set F is called a finite support of
$\mathcal {F}$
. In this case the set F is called a finite support of
![]() $\mathcal {N}$
over
$\mathcal {N}$
over
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
We will be working with finitely supported, one-point extensions of continuous
![]() $\mathcal {L}$
-pre-structures. In the following first step, we focus on one-point extensions.
$\mathcal {L}$
-pre-structures. In the following first step, we focus on one-point extensions.
4.1. One-point extensions
In this subsection we study one-point extensions of continuous
![]() $\mathcal {L}$
-pre-structures and their amalgams.
$\mathcal {L}$
-pre-structures and their amalgams.
Fix a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
. If
$\mathcal {M}$
. If
![]() $\mathcal {N}$
is a one-point extension of
$\mathcal {N}$
is a one-point extension of
![]() $\mathcal {M}$
, we denote the unique element of
$\mathcal {M}$
, we denote the unique element of
![]() $N\setminus M$
by
$N\setminus M$
by
![]() $x_{\mathcal {N}}$
. Conversely, if x is the unique element of
$x_{\mathcal {N}}$
. Conversely, if x is the unique element of
![]() $N\setminus M$
, we also denote
$N\setminus M$
, we also denote
![]() $\mathcal {N}$
by
$\mathcal {N}$
by
![]() $\mathcal {M}_x$
.
$\mathcal {M}_x$
.
If
![]() $\mathcal {M}_x$
and
$\mathcal {M}_x$
and
![]() $\mathcal {M}_y$
are two one-point extensions of
$\mathcal {M}_y$
are two one-point extensions of
![]() $\mathcal {M}$
, consider the map
$\mathcal {M}$
, consider the map
![]() ${\varphi : M_x\to M_y}$
with
${\varphi : M_x\to M_y}$
with
![]() $\varphi (x)=y$
and
$\varphi (x)=y$
and
![]() $\varphi (z)=z$
for all
$\varphi (z)=z$
for all
![]() $z\in M$
. Define an equivalence relation
$z\in M$
. Define an equivalence relation
![]() $x\sim y$
if
$x\sim y$
if
![]() $\varphi $
is an isomorphism between
$\varphi $
is an isomorphism between
![]() $\mathcal {M}_x$
and
$\mathcal {M}_x$
and
![]() $\mathcal {M}_y$
as continuous
$\mathcal {M}_y$
as continuous
![]() $\mathcal {L}$
-pre-structures.
$\mathcal {L}$
-pre-structures.
Let
![]() $\tilde {E}(\mathcal {M})$
be the collection of all
$\tilde {E}(\mathcal {M})$
be the collection of all
![]() $x_{\mathcal {N}}$
for one-point extensions
$x_{\mathcal {N}}$
for one-point extensions
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $E'(\mathcal {M})$
be the quotient space
$E'(\mathcal {M})$
be the quotient space
![]() $\tilde {E}(\mathcal {M})/\!\sim $
. In
$\tilde {E}(\mathcal {M})/\!\sim $
. In
![]() $E'(\mathcal {M})$
we identify
$E'(\mathcal {M})$
we identify
![]() $\sim $
-equivalent x and y and consider them the same object, and write
$\sim $
-equivalent x and y and consider them the same object, and write
![]() $x=y$
. Finally, let
$x=y$
. Finally, let
be the disjoint union of M and
![]() $E'(\mathcal {M})$
.
$E'(\mathcal {M})$
.
We define a continuous
![]() $\mathcal {L}$
-pre-structure on
$\mathcal {L}$
-pre-structure on
![]() $E(\mathcal {M})$
as follows. For any
$E(\mathcal {M})$
as follows. For any
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $x, y\in E(\mathcal {M})$
and
$x, y\in E(\mathcal {M})$
and
![]() $\overline {u}=(u_1,\dots , u_n)\in E(\mathcal {M})^n$
, define
$\overline {u}=(u_1,\dots , u_n)\in E(\mathcal {M})^n$
, define
![]() $\overline {u}(y|x)=(v_1,\dots , v_n)\in E(\mathcal {M})^n$
by letting, for
$\overline {u}(y|x)=(v_1,\dots , v_n)\in E(\mathcal {M})^n$
by letting, for
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $$ \begin{align*}v_i=\left\{\begin{array}{@{}ll} u_i, & \mbox{ if}\ u_i\neq x, \\ y, & \mbox{ if}\ u_i=x. \end{array}\right.\end{align*} $$
$$ \begin{align*}v_i=\left\{\begin{array}{@{}ll} u_i, & \mbox{ if}\ u_i\neq x, \\ y, & \mbox{ if}\ u_i=x. \end{array}\right.\end{align*} $$
Also, for
![]() $\overline {u}\in E(\mathcal {M})^n$
, let
$\overline {u}\in E(\mathcal {M})^n$
, let
For
![]() $x, y\in E(\mathcal {M})$
, define a metric
$x, y\in E(\mathcal {M})$
, define a metric
![]() $d^E(x,y)$
so that
$d^E(x,y)$
so that
 $$ \begin{align*}d^E(x, y)=\left\{\begin{array}{@{}ll} d^M(x,y), & \mbox{ if}\ x, y\in M, \\ d^{M_x}(x, y), & \mbox{ if}\ x\in E'(\mathcal{M}) \mbox{ and}\ y\in M, \\ d^{M_y}(x,y), & \mbox{ if}\ x\in M\ \mbox{ and}\ y\in E'(\mathcal{M}).\end{array}\right.\end{align*} $$
$$ \begin{align*}d^E(x, y)=\left\{\begin{array}{@{}ll} d^M(x,y), & \mbox{ if}\ x, y\in M, \\ d^{M_x}(x, y), & \mbox{ if}\ x\in E'(\mathcal{M}) \mbox{ and}\ y\in M, \\ d^{M_y}(x,y), & \mbox{ if}\ x\in M\ \mbox{ and}\ y\in E'(\mathcal{M}).\end{array}\right.\end{align*} $$
If
![]() $x, y\in E'(\mathcal {M})$
, we define
$x, y\in E'(\mathcal {M})$
, we define
 $$ \begin{align*} \mu(x,y) &= \max\left\{\mathfrak{u}_{R,1}^*(|R^{M_x}(x)-R^{M_y}(y)|)\,:\, R\in\mathcal{L} \mbox{ is unary}\right\}, \\\rho(x, y)&=\sup\left\{ \|\overline{u}\|^{-1}|R^{M_x}(\overline{u})-R^{M_y}(\overline{u}(y|x))|\ :\right.\\& \qquad\qquad \overline{u}\in M_x^n\setminus M^n, R\in {\mathcal{L}} \mbox{ is}\ n\text{-}\mbox{ary for}\ n\geq 2\big\},\\\lambda(x,y)&=\sup\left\{|d^{M_x}(x, z)-d^{M_y}(y,z)|\,:\, z\in M\right\}, \end{align*} $$
$$ \begin{align*} \mu(x,y) &= \max\left\{\mathfrak{u}_{R,1}^*(|R^{M_x}(x)-R^{M_y}(y)|)\,:\, R\in\mathcal{L} \mbox{ is unary}\right\}, \\\rho(x, y)&=\sup\left\{ \|\overline{u}\|^{-1}|R^{M_x}(\overline{u})-R^{M_y}(\overline{u}(y|x))|\ :\right.\\& \qquad\qquad \overline{u}\in M_x^n\setminus M^n, R\in {\mathcal{L}} \mbox{ is}\ n\text{-}\mbox{ary for}\ n\geq 2\big\},\\\lambda(x,y)&=\sup\left\{|d^{M_x}(x, z)-d^{M_y}(y,z)|\,:\, z\in M\right\}, \end{align*} $$
and
Lemma 4.3.
![]() $d^E$
is a metric on
$d^E$
is a metric on
![]() $E(\mathcal {M})$
.
$E(\mathcal {M})$
.
Proof We verify that if
![]() $d^E(x,y)=0$
then
$d^E(x,y)=0$
then
![]() $x=y$
. This is clear when at least one of
$x=y$
. This is clear when at least one of
![]() $x, y$
is in M. Assume
$x, y$
is in M. Assume
![]() $x, y\in E'(\mathcal {M})$
. Let
$x, y\in E'(\mathcal {M})$
. Let
![]() $\varphi : M_x\to M_y$
be the map with
$\varphi : M_x\to M_y$
be the map with
![]() $\varphi (x)=y$
and
$\varphi (x)=y$
and
![]() $\varphi (z)=z$
for all
$\varphi (z)=z$
for all
![]() $z\in M$
. If
$z\in M$
. If
![]() $d^E(x,y)=0$
then
$d^E(x,y)=0$
then
![]() $\mu (x,y)=\rho (x,y)=\lambda (x,y)=0$
, which implies that
$\mu (x,y)=\rho (x,y)=\lambda (x,y)=0$
, which implies that
![]() $\varphi $
is an isomorphism between
$\varphi $
is an isomorphism between
![]() $\mathcal {M}_x$
and
$\mathcal {M}_x$
and
![]() $\mathcal {M}_y$
as continuous
$\mathcal {M}_y$
as continuous
![]() $\mathcal {L}$
-pre-structures. Thus
$\mathcal {L}$
-pre-structures. Thus
![]() $x=y$
.
$x=y$
.
Note that
![]() $\mu $
satisfies the triangle inequality because by Lemma 2.3
$\mu $
satisfies the triangle inequality because by Lemma 2.3
![]() $\mathfrak {u}_{R,1}^*$
is subadditive for unary
$\mathfrak {u}_{R,1}^*$
is subadditive for unary
![]() $R\in \mathcal {L}$
. For all
$R\in \mathcal {L}$
. For all
![]() $x, y, z\in E'(\mathcal {M})$
,
$x, y, z\in E'(\mathcal {M})$
,
![]() $d(x, y)+d(y, z)\geq d(x, z)$
, because all of
$d(x, y)+d(y, z)\geq d(x, z)$
, because all of
![]() $\mu $
,
$\mu $
,
![]() $\rho $
and
$\rho $
and
![]() $\lambda $
satisfy the triangle inequality. Also, it is easy to verify that
$\lambda $
satisfy the triangle inequality. Also, it is easy to verify that
![]() $\max \{\mu (x, y), \rho (x, y), \lambda (x, y)\}\leq \inf \left\{d^{M_x}(x, z)+d^{M_y}(y, z)\,:\, z\in M\right\}$
, thus
$\max \{\mu (x, y), \rho (x, y), \lambda (x, y)\}\leq \inf \left\{d^{M_x}(x, z)+d^{M_y}(y, z)\,:\, z\in M\right\}$
, thus
![]() $d^E$
also satisfies the triangle inequality.
$d^E$
also satisfies the triangle inequality.
Define
![]() $(X, d^X)=(E(\mathcal {M}), d^E)$
and for any n-ary
$(X, d^X)=(E(\mathcal {M}), d^E)$
and for any n-ary
![]() $R\in \mathcal {L}$
define
$R\in \mathcal {L}$
define
![]() $R^X$
naturally on
$R^X$
naturally on
Lemma 4.4.
![]() $\mathcal {X}=(X, d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
$\mathcal {X}=(X, d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure.
$\mathcal {L}$
-pre-structure.
Proof We verify that for any n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^X$
is
$R^X$
is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $d^X_R$
.
$d^X_R$
.
Suppose first
![]() $n=1$
. It suffices to show that for any
$n=1$
. It suffices to show that for any
![]() $x, y\in E'(\mathcal {M})$
,
$x, y\in E'(\mathcal {M})$
,
For this, note that by Lemma 2.3(3), we have
 $$ \begin{align*} |R^X(x)-R^X(y)|&=|R^{M_x}(x)-R^{M_y}(y)| \\&\leq \mathfrak{u}_{R,1}(\mathfrak{u}_{R,1}^*(|R^{M_x}(x)-R^{M_y}(y)|)) \\&\leq \mathfrak{u}_{R,1}(\mu(x,y)) \\&\leq \mathfrak{u}_{R,1}(d^X(x,y)). \end{align*} $$
$$ \begin{align*} |R^X(x)-R^X(y)|&=|R^{M_x}(x)-R^{M_y}(y)| \\&\leq \mathfrak{u}_{R,1}(\mathfrak{u}_{R,1}^*(|R^{M_x}(x)-R^{M_y}(y)|)) \\&\leq \mathfrak{u}_{R,1}(\mu(x,y)) \\&\leq \mathfrak{u}_{R,1}(d^X(x,y)). \end{align*} $$
Next suppose
![]() $n\geq 2$
. The statement follows from Lemma 3.5 in all cases except when
$n\geq 2$
. The statement follows from Lemma 3.5 in all cases except when
![]() $\overline {u}\in M^n_x\setminus M^n, \overline {v}\in M_y^n\setminus M^n$
for distinct
$\overline {u}\in M^n_x\setminus M^n, \overline {v}\in M_y^n\setminus M^n$
for distinct
![]() $x, y\in E'(\mathcal {M})$
.
$x, y\in E'(\mathcal {M})$
.
Suppose
![]() $\overline {u}=(u_1,\dots , u_n),\overline {v}=(v_1,\dots , v_n)$
are given as above. Let
$\overline {u}=(u_1,\dots , u_n),\overline {v}=(v_1,\dots , v_n)$
are given as above. Let
 $$ \begin{align*} S_0&= \{ i\,:\, u_i, v_i\in M\}, \\S_1&= \{i\,:\, u_i=x, v_i\in M\}, \\S_2&= \{i\,:\, u_i\in M, v_i=y\}, \\S_3&= \{i\,:\, u_i=x, v_i=y\}. \end{align*} $$
$$ \begin{align*} S_0&= \{ i\,:\, u_i, v_i\in M\}, \\S_1&= \{i\,:\, u_i=x, v_i\in M\}, \\S_2&= \{i\,:\, u_i\in M, v_i=y\}, \\S_3&= \{i\,:\, u_i=x, v_i=y\}. \end{align*} $$
Define
![]() $\overline {w}=(w_1,\dots , w_n)\in M_x^n$
by
$\overline {w}=(w_1,\dots , w_n)\in M_x^n$
by
 $$ \begin{align*}w_i=\left\{\begin{array}{@{}ll}u_i, & \mbox{ if}\ i\in S_2\cup S_3,\\ v_i, & \mbox{ if}\ i\in S_0\cup S_1. \end{array}\right. \end{align*} $$
$$ \begin{align*}w_i=\left\{\begin{array}{@{}ll}u_i, & \mbox{ if}\ i\in S_2\cup S_3,\\ v_i, & \mbox{ if}\ i\in S_0\cup S_1. \end{array}\right. \end{align*} $$
Then
 $$ \begin{align*}& |R^X(\overline{u})-R^X(\overline{v})| \\& \quad \leq |R^X(\overline{u})-R^X(\overline{w})|+|R^X(\overline{w})-R^X(\overline{w}(y|x))|+|R^X(\overline{w}(y|x))-R^X(\overline{v})| \\& \quad \leq d^X_R(\overline{u},\overline{w})+\|w\|\rho(x, y)+d^X_R(\overline{w}(y|x),\overline{v}) \\& \quad \leq \displaystyle\sum_{i\in S_0\cup S_1}K_{R,i}d^X(u_i,v_i)+\sum_{i\in S_3}K_{R,i}d^X(u_i,v_i)+\sum_{i\in S_2} K_{R,i}d^X(u_i,v_i) \\& \quad = d^X_R(\overline{u},\overline{v}) \end{align*} $$
$$ \begin{align*}& |R^X(\overline{u})-R^X(\overline{v})| \\& \quad \leq |R^X(\overline{u})-R^X(\overline{w})|+|R^X(\overline{w})-R^X(\overline{w}(y|x))|+|R^X(\overline{w}(y|x))-R^X(\overline{v})| \\& \quad \leq d^X_R(\overline{u},\overline{w})+\|w\|\rho(x, y)+d^X_R(\overline{w}(y|x),\overline{v}) \\& \quad \leq \displaystyle\sum_{i\in S_0\cup S_1}K_{R,i}d^X(u_i,v_i)+\sum_{i\in S_3}K_{R,i}d^X(u_i,v_i)+\sum_{i\in S_2} K_{R,i}d^X(u_i,v_i) \\& \quad = d^X_R(\overline{u},\overline{v}) \end{align*} $$
as required.
By Lemma 3.7 we obtain a continuous
![]() $\mathcal {L}$
-pre-structure which is a conservative extension of
$\mathcal {L}$
-pre-structure which is a conservative extension of
![]() $\mathcal {X}$
. We denote this continuous
$\mathcal {X}$
. We denote this continuous
![]() $\mathcal {L}$
-pre-structure as
$\mathcal {L}$
-pre-structure as
From the proof of Lemma 3.7, we have that for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {x}\in E(\mathcal {M})^n$
,
$\overline {x}\in E(\mathcal {M})^n$
,
4.2. Finitely-supported one-point extensions
In this subsection we turn to finitely-supported one-point extensions.
Suppose
![]() $\mathcal {M}_x$
is a one-point extension of
$\mathcal {M}_x$
is a one-point extension of
![]() $\mathcal {M}$
with finite support
$\mathcal {M}$
with finite support
![]() $F\subseteq M$
. Then
$F\subseteq M$
. Then
![]() $\mathcal {M}_x$
is a canonical amalgam of
$\mathcal {M}_x$
is a canonical amalgam of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {F}_x$
over
$\mathcal {F}_x$
over
![]() $\mathcal {F}$
. This implies that for any
$\mathcal {F}$
. This implies that for any
![]() $y\in M$
,
$y\in M$
,
and for any n-ary
![]() $R\in \mathcal {L}$
where
$R\in \mathcal {L}$
where
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $\overline {u}\in M_x^n$
,
$\overline {u}\in M_x^n$
,
We define
and let
![]() $\mathcal {E}(\mathcal {M},\omega )$
be the substructure of
$\mathcal {E}(\mathcal {M},\omega )$
be the substructure of
![]() $\mathcal {E}(\mathcal {M})$
with domain
$\mathcal {E}(\mathcal {M})$
with domain
![]() $E(\mathcal {M},\omega )$
.
$E(\mathcal {M},\omega )$
.
Theorem 4.5. Let
![]() $\mathcal {L}$
be a proper continuous signature and
$\mathcal {L}$
be a proper continuous signature and
![]() $\mathcal {M}$
be a continuous
$\mathcal {M}$
be a continuous
![]() $\mathcal {L}$
-pre-structure. If
$\mathcal {L}$
-pre-structure. If
![]() $\mathcal {M}$
is separable, then so is
$\mathcal {M}$
is separable, then so is
![]() $\mathcal {E}(\mathcal {M},\omega )$
.
$\mathcal {E}(\mathcal {M},\omega )$
.
Proof Let N be the largest arity of all
![]() $R\in \mathcal {L}$
. Let K be the least of all
$R\in \mathcal {L}$
. Let K be the least of all
![]() $K_{R,i}$
for n-ary
$K_{R,i}$
for n-ary
![]() $R\in \mathcal {L}$
where
$R\in \mathcal {L}$
where
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1\leq i\leq n$
. Let J be the largest value of all
$1\leq i\leq n$
. Let J be the largest value of all
![]() $K_{R,i}/K$
for n-ary
$K_{R,i}/K$
for n-ary
![]() $R\in \mathcal {L}$
where
$R\in \mathcal {L}$
where
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
Let D be a countable dense subset of M. Let
and let G be the additive subgroup of
![]() $\mathbb {R}$
generated by
$\mathbb {R}$
generated by
![]() $V\cup \mathbb {Q}$
. Then G is a countable dense subset of
$V\cup \mathbb {Q}$
. Then G is a countable dense subset of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
We say that a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {A}$
is G-valued if
$\mathcal {A}$
is G-valued if
Let
Then
![]() $B\subseteq E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
is countable. It suffices to show that B is dense in
$B\subseteq E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
is countable. It suffices to show that B is dense in
![]() $E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
.
$E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
.
Let
![]() $x\in E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
and
$x\in E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
and
![]() $1>\epsilon >0$
. Suppose
$1>\epsilon >0$
. Suppose
![]() $A=\{a_0, \dots , a_m\}\subseteq M$
is a finite support of
$A=\{a_0, \dots , a_m\}\subseteq M$
is a finite support of
![]() $\mathcal {M}_x$
such that
$\mathcal {M}_x$
such that
Let
Choose
 $$ \begin{align*}0<\epsilon_0<\displaystyle\frac{\epsilon\min\{1,\delta\}\min\{1,K\}}{(9m+9)N}.\end{align*} $$
$$ \begin{align*}0<\epsilon_0<\displaystyle\frac{\epsilon\min\{1,\delta\}\min\{1,K\}}{(9m+9)N}.\end{align*} $$
Then
 $$ \begin{align*}\epsilon_0<\min\left\{\displaystyle\frac{\min\{\epsilon, \delta\}}{9m+9}, \frac{\epsilon\delta}{(9m+9)N}, \frac{K\epsilon\delta}{4}\right\}.\end{align*} $$
$$ \begin{align*}\epsilon_0<\min\left\{\displaystyle\frac{\min\{\epsilon, \delta\}}{9m+9}, \frac{\epsilon\delta}{(9m+9)N}, \frac{K\epsilon\delta}{4}\right\}.\end{align*} $$
Since D is dense, we can find distinct
![]() $b_0,\dots , b_m\in D$
such that
$b_0,\dots , b_m\in D$
such that
for all
![]() $0\leq i\leq m$
. Let
$0\leq i\leq m$
. Let
![]() $F=\{b_0,\dots , b_m\}\subseteq D$
.
$F=\{b_0,\dots , b_m\}\subseteq D$
.
Define
![]() $g: F\to G$
by
$g: F\to G$
by
for
![]() $0\leq i\leq m$
, where we choose
$0\leq i\leq m$
, where we choose
![]() $\epsilon _i'\in (0,\epsilon _0)$
so that
$\epsilon _i'\in (0,\epsilon _0)$
so that
![]() $g(b_i)\in G$
. Then the following computations demonstrate that for all
$g(b_i)\in G$
. Then the following computations demonstrate that for all
![]() $0\leq i<j\leq m$
,
$0\leq i<j\leq m$
,
Indeed, suppose
![]() $0\leq i<j\leq m$
. We have
$0\leq i<j\leq m$
. We have
 $$ \begin{align*} g(b_j)-g(b_i)&= d^{M_x}(x, a_j)-d^{M_x}(x, a_i)+3(j-i)\epsilon_0+\epsilon_j'-\epsilon_i' \\&< (3m+1)\epsilon_0 \\&= 3(m+1)\epsilon_0-2\epsilon_0 \\&< \delta-(d^M(a_i, b_i)+d^M(a_j,b_j)) \\&\leq d^M(a_i, a_j)-d^M(a_i,b_i)-d^M(a_j, b_j) \\&\leq d^M(b_i,b_j),\\g(b_i)-g(b_j)&= d^{M_x}(x, a_i)-d^{M_x}(x, a_j)-3(j-i)\epsilon_0+\epsilon_i'-\epsilon_j' \\&\leq d^{M_x}(x, a_i)-d^{M_x}(x, a_j)-2\epsilon_0 \\&< d^M(a_i,a_j)-d^M(a_i, b_i)-d^M(a_j, b_j) \\&\leq d^M(b_i,b_j), \end{align*} $$
$$ \begin{align*} g(b_j)-g(b_i)&= d^{M_x}(x, a_j)-d^{M_x}(x, a_i)+3(j-i)\epsilon_0+\epsilon_j'-\epsilon_i' \\&< (3m+1)\epsilon_0 \\&= 3(m+1)\epsilon_0-2\epsilon_0 \\&< \delta-(d^M(a_i, b_i)+d^M(a_j,b_j)) \\&\leq d^M(a_i, a_j)-d^M(a_i,b_i)-d^M(a_j, b_j) \\&\leq d^M(b_i,b_j),\\g(b_i)-g(b_j)&= d^{M_x}(x, a_i)-d^{M_x}(x, a_j)-3(j-i)\epsilon_0+\epsilon_i'-\epsilon_j' \\&\leq d^{M_x}(x, a_i)-d^{M_x}(x, a_j)-2\epsilon_0 \\&< d^M(a_i,a_j)-d^M(a_i, b_i)-d^M(a_j, b_j) \\&\leq d^M(b_i,b_j), \end{align*} $$
and
 $$ \begin{align*} d^M(b_i,b_j)& \leq d^{M_x}(x, a_i)+d^{M_x}(x, a_j)+d^M(a_i, b_i)+d^M(a_j, b_j) \\& < d^{M_x}(x, a_i)+d^{M_x}(x, a_j)+2\epsilon_0 \\& < g(b_i)+g(b_j). \end{align*} $$
$$ \begin{align*} d^M(b_i,b_j)& \leq d^{M_x}(x, a_i)+d^{M_x}(x, a_j)+d^M(a_i, b_i)+d^M(a_j, b_j) \\& < d^{M_x}(x, a_i)+d^{M_x}(x, a_j)+2\epsilon_0 \\& < g(b_i)+g(b_j). \end{align*} $$
We can thus define a one-point extension of the finite metric space
![]() $(F,d^F)$
by a point u such that for all
$(F,d^F)$
by a point u such that for all
![]() $0\leq i\leq m$
,
$0\leq i\leq m$
,
![]() $d^{F_u}(u, b_i)=g(b_i)$
. By defining
$d^{F_u}(u, b_i)=g(b_i)$
. By defining
for any
![]() $y\in M$
, we extend the metric to
$y\in M$
, we extend the metric to
![]() $M_u=M\cup \{u\}$
.
$M_u=M\cup \{u\}$
.
Next we define a continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {F}_u$
with domain
$\mathcal {F}_u$
with domain
![]() $F_u=F\cup \{u\}$
by defining the values of
$F_u=F\cup \{u\}$
by defining the values of
![]() $R^{F_u}$
for all
$R^{F_u}$
for all
![]() $R\in \mathcal {L}$
.
$R\in \mathcal {L}$
.
Suppose first
![]() $R\in \mathcal {L}$
is unary. Since G is dense in
$R\in \mathcal {L}$
is unary. Since G is dense in
![]() $\mathbb {R}$
, we may choose
$\mathbb {R}$
, we may choose
![]() $R^{F_u}(u)\in G\cap [0,1]$
such that
$R^{F_u}(u)\in G\cap [0,1]$
such that
We verify that (UCℒ
) holds for R in
![]() $F_u$
. In fact, for any
$F_u$
. In fact, for any
![]() $0\leq i\leq m$
, if
$0\leq i\leq m$
, if
![]() $g(b_i)\in I_{R,1}$
, then by the superadditivity of
$g(b_i)\in I_{R,1}$
, then by the superadditivity of
![]() $\mathfrak {u}_{R,1}$
, we have
$\mathfrak {u}_{R,1}$
, we have
 $$ \begin{align*} & |R^M(b_i)-R^{F_u}(u)| \\&\quad \leq |R^M(b_i)-R^M(a_i)|+|R^M(a_i)-R^{M_x}(x)|+|R^{M_x}(x)-R^{F_u}(u)| \\&\quad \leq \mathfrak{u}_{R,1}(d^M(b_i,a_i))+\mathfrak{u}_{R,1}(d^{M_x}(x, a_i))+\mathfrak{u}_{R,1}(\frac{\epsilon}{2}) \\&\quad \leq \mathfrak{u}_{R,1}(\epsilon_0)+\mathfrak{u}_{R,1}(d^{M_x}(x, a_i))+\mathfrak{u}_{R,1}(\frac{\epsilon}{2}) \\&\quad \leq \mathfrak{u}_{R,1}(g(b_i))=\mathfrak{u}_{R,1}(d^{F_u}(u,b_i)). \end{align*} $$
$$ \begin{align*} & |R^M(b_i)-R^{F_u}(u)| \\&\quad \leq |R^M(b_i)-R^M(a_i)|+|R^M(a_i)-R^{M_x}(x)|+|R^{M_x}(x)-R^{F_u}(u)| \\&\quad \leq \mathfrak{u}_{R,1}(d^M(b_i,a_i))+\mathfrak{u}_{R,1}(d^{M_x}(x, a_i))+\mathfrak{u}_{R,1}(\frac{\epsilon}{2}) \\&\quad \leq \mathfrak{u}_{R,1}(\epsilon_0)+\mathfrak{u}_{R,1}(d^{M_x}(x, a_i))+\mathfrak{u}_{R,1}(\frac{\epsilon}{2}) \\&\quad \leq \mathfrak{u}_{R,1}(g(b_i))=\mathfrak{u}_{R,1}(d^{F_u}(u,b_i)). \end{align*} $$
If
![]() $g(b_i)\not \in I_{R,1}$
then
$g(b_i)\not \in I_{R,1}$
then
Next suppose
![]() $R\in \mathcal {L}$
is n-ary for
$R\in \mathcal {L}$
is n-ary for
![]() $n\geq 2$
. If
$n\geq 2$
. If
![]() $\overline {v}\in F^n$
, then let
$\overline {v}\in F^n$
, then let
![]() $R^{F_u}(\overline {v})=R^M(\overline {v})$
. Next we define
$R^{F_u}(\overline {v})=R^M(\overline {v})$
. Next we define
![]() $R^{F_u}(\overline {v})$
for
$R^{F_u}(\overline {v})$
for
![]() $\overline {v}=(v_1,\dots , v_n)\in F_u^n\setminus F^n$
. For this, let
$\overline {v}=(v_1,\dots , v_n)\in F_u^n\setminus F^n$
. For this, let
![]() $\overline {v}'=(v_1',\dots , v_n')\in A_x^n\setminus A^n$
be defined by
$\overline {v}'=(v_1',\dots , v_n')\in A_x^n\setminus A^n$
be defined by
 $$ \begin{align*}v_i'=\left\{\begin{array}{@{}ll} a_j, & \mbox{ if}\ v_i=b_j, \\ x, & \mbox{ if}\ v_i=u.\end{array}\right.\end{align*} $$
$$ \begin{align*}v_i'=\left\{\begin{array}{@{}ll} a_j, & \mbox{ if}\ v_i=b_j, \\ x, & \mbox{ if}\ v_i=u.\end{array}\right.\end{align*} $$
We define
![]() $R^{F_u}: F_u^n\setminus F^n\to G\cap [0,1]$
such that:
$R^{F_u}: F_u^n\setminus F^n\to G\cap [0,1]$
such that:
-
(a) for all
 $\overline {v}\in F_u^n\setminus F^n$
,
$\overline {v}\in F_u^n\setminus F^n$
,
 $|R^{F_u}(\overline {v})-R^{A_x}(\overline {v}')|<K\displaystyle \frac {\epsilon }{2}$
, and
$|R^{F_u}(\overline {v})-R^{A_x}(\overline {v}')|<K\displaystyle \frac {\epsilon }{2}$
, and -
(b) for all
 $\overline {v}, \overline {w}\in F_u^n\setminus F^n$
,
$\overline {v}, \overline {w}\in F_u^n\setminus F^n$
,  $$ \begin{align*}|R^{F_u}(\overline{v})-R^{F_u}(\overline{w})|\leq \left( 1-\displaystyle\frac{\epsilon_0}{\delta}\right) |R^{A_x}(\overline{v}')-R^{A_x}(\overline{w}')|.\end{align*} $$
$$ \begin{align*}|R^{F_u}(\overline{v})-R^{F_u}(\overline{w})|\leq \left( 1-\displaystyle\frac{\epsilon_0}{\delta}\right) |R^{A_x}(\overline{v}')-R^{A_x}(\overline{w}')|.\end{align*} $$
Note that our choice of
![]() $\epsilon _0$
guarantees that
$\epsilon _0$
guarantees that
To define
![]() $R^{F_u}$
we enumerate all elements of
$R^{F_u}$
we enumerate all elements of
![]() $F_u^n\setminus F^n$
as
$F_u^n\setminus F^n$
as
such that
If
![]() $R^{A_x}({\overline {v}^i}')=0$
we define
$R^{A_x}({\overline {v}^i}')=0$
we define
![]() $R^{F_u}(\overline {v})=0$
. We also make the commitment that if
$R^{F_u}(\overline {v})=0$
. We also make the commitment that if
![]() $R^{A_x}({\overline {v}^i}')=R^{A_x}({\overline {v}^j}')$
then
$R^{A_x}({\overline {v}^i}')=R^{A_x}({\overline {v}^j}')$
then
![]() $R^{F_u}(\overline {v}^i)=R^{F_u}(\overline {v}^j)$
. With this commitment we assume without loss of generality that
$R^{F_u}(\overline {v}^i)=R^{F_u}(\overline {v}^j)$
. With this commitment we assume without loss of generality that
We will then make our definition by induction on
![]() $i=0,\dots , \ell $
with the following inductive hypotheses:
$i=0,\dots , \ell $
with the following inductive hypotheses:
-
(H1)
 $R^{F_u}(\overline {v}^i)\in G$
and
$R^{F_u}(\overline {v}^i)\in G$
and  $$ \begin{align*}\left(1-\displaystyle\frac{2\epsilon_0}{\delta}\right) R^{A_x}({\overline{v}^i}')< R^{F_u}(\overline{v}^i)<\left(1-\displaystyle\frac{\epsilon_0}{\delta}\right) R^{A_x}({\overline{v}^i}');\end{align*} $$
$$ \begin{align*}\left(1-\displaystyle\frac{2\epsilon_0}{\delta}\right) R^{A_x}({\overline{v}^i}')< R^{F_u}(\overline{v}^i)<\left(1-\displaystyle\frac{\epsilon_0}{\delta}\right) R^{A_x}({\overline{v}^i}');\end{align*} $$
-
(H2) for all
 $j<i$
,
$j<i$
,  $$ \begin{align*}R^{F_u}(\overline{v}^i)\leq R^{F_u}(\overline{v}^j)+\left(1-\displaystyle\frac{\epsilon_0}{\delta}\right)(R^{A_x}({\overline{v}^i}')-R^{A_x}({\overline{v}^j}')).\end{align*} $$
$$ \begin{align*}R^{F_u}(\overline{v}^i)\leq R^{F_u}(\overline{v}^j)+\left(1-\displaystyle\frac{\epsilon_0}{\delta}\right)(R^{A_x}({\overline{v}^i}')-R^{A_x}({\overline{v}^j}')).\end{align*} $$
For
![]() $i=0$
(H2) is vacuous and (H1) can be accomplished by the density of G. In general, suppose we have defined
$i=0$
(H2) is vacuous and (H1) can be accomplished by the density of G. In general, suppose we have defined
![]() $R^{F_u}(\overline {v}^j)$
for
$R^{F_u}(\overline {v}^j)$
for
![]() $j\leq i$
to satisfy (H1) and (H2). Note that
$j\leq i$
to satisfy (H1) and (H2). Note that
 $$ \begin{align*}\left(1-\displaystyle\frac{2\epsilon_0}{\delta}\right) R^{A_x}({\overline{v}^{i+1}}')<R^{F_u}(\overline{v}^i)+\left(1-\displaystyle\frac{\epsilon_0}{\delta}\right)(R^{A_x}({\overline{v}^{i+1}}')-R^{A_x}({\overline{v}^i}')).\end{align*} $$
$$ \begin{align*}\left(1-\displaystyle\frac{2\epsilon_0}{\delta}\right) R^{A_x}({\overline{v}^{i+1}}')<R^{F_u}(\overline{v}^i)+\left(1-\displaystyle\frac{\epsilon_0}{\delta}\right)(R^{A_x}({\overline{v}^{i+1}}')-R^{A_x}({\overline{v}^i}')).\end{align*} $$
We can then define
![]() $R^{F_u}(\overline {v}^{i+1})\in G$
to be a value in between the above two quantities. To see that the inductive hypotheses are maintained, note that by this definition (H2) and the left half of (H1) are immediate. For the right half of (H1), just note that
$R^{F_u}(\overline {v}^{i+1})\in G$
to be a value in between the above two quantities. To see that the inductive hypotheses are maintained, note that by this definition (H2) and the left half of (H1) are immediate. For the right half of (H1), just note that
This finishes the definition of
![]() $R^{F_u}$
. It is easy to see that (a) and (b) hold.
$R^{F_u}$
. It is easy to see that (a) and (b) hold.
We verify (UCℒ
) for R in
![]() $F_u$
. For this, let
$F_u$
. For this, let
![]() $\overline {v},\overline {w}\in F_u^n$
differ at exactly one coordinate, say the ith coordinate. If both
$\overline {v},\overline {w}\in F_u^n$
differ at exactly one coordinate, say the ith coordinate. If both
![]() $\overline {v},\overline {w}\in F^n$
then
$\overline {v},\overline {w}\in F^n$
then
by the (UCℒ
) for R in M. If both
![]() $\overline {v},\overline {w}\in F_u^n\setminus F^n$
, then by (b) we have
$\overline {v},\overline {w}\in F_u^n\setminus F^n$
, then by (b) we have
 $$ \begin{align*} |R^{F_u}(\overline{v})-R^{F_u}(\overline{w})|&\leq \left( 1-\displaystyle\frac{\epsilon_0}{\delta}\right) |R^{A_x}(\overline{v}')-R^{A_x}(\overline{w}')| \\&\leq \left( 1-\displaystyle\frac{\epsilon_0}{\delta}\right)K_{R,i}d^{A_x}(v_i', w_i') \\&\leq K_{R,i}d^{A_x}(v_i',w_i') -K_{R,i}\epsilon_0. \end{align*} $$
$$ \begin{align*} |R^{F_u}(\overline{v})-R^{F_u}(\overline{w})|&\leq \left( 1-\displaystyle\frac{\epsilon_0}{\delta}\right) |R^{A_x}(\overline{v}')-R^{A_x}(\overline{w}')| \\&\leq \left( 1-\displaystyle\frac{\epsilon_0}{\delta}\right)K_{R,i}d^{A_x}(v_i', w_i') \\&\leq K_{R,i}d^{A_x}(v_i',w_i') -K_{R,i}\epsilon_0. \end{align*} $$
Now if
![]() $v_i, w_i\in F$
then we have
$v_i, w_i\in F$
then we have
![]() $v_i', w_i'\in A$
,
$v_i', w_i'\in A$
,
![]() $d^{A_x}(v_i', w_i')=d^M(v_i', w_i')$
,
$d^{A_x}(v_i', w_i')=d^M(v_i', w_i')$
,
and
 $$ \begin{align*} |R^{F_u}(\overline{v})-R^{F_u}(\overline{w})|&\leq K_{R,i}d^M(v_i',w_i')-K_{R,i}\epsilon_0 \\& \leq K_{R,i}d^M(v_i', w_i')-K_{R,i}(d^M(v_i',v_i)+d^M(w_i',w_i)) \\&\leq K_{R,i}d^M(v_i, w_i). \end{align*} $$
$$ \begin{align*} |R^{F_u}(\overline{v})-R^{F_u}(\overline{w})|&\leq K_{R,i}d^M(v_i',w_i')-K_{R,i}\epsilon_0 \\& \leq K_{R,i}d^M(v_i', w_i')-K_{R,i}(d^M(v_i',v_i)+d^M(w_i',w_i)) \\&\leq K_{R,i}d^M(v_i, w_i). \end{align*} $$
If
![]() $v_i\in F$
and
$v_i\in F$
and
![]() $w_i=u$
, then
$w_i=u$
, then
![]() $v_i'\in A$
and
$v_i'\in A$
and
![]() $w_i'=x$
, and
$w_i'=x$
, and
This finishes the proof of (UCℒ
) for R for the case
![]() $\overline {v},\overline {w}\in F_u^n\setminus F^n$
. Finally, suppose
$\overline {v},\overline {w}\in F_u^n\setminus F^n$
. Finally, suppose
![]() $\overline {v}\in F_u^n\setminus F^n$
and
$\overline {v}\in F_u^n\setminus F^n$
and
![]() $\overline {w}\in F^n$
. Since
$\overline {w}\in F^n$
. Since
![]() $\overline {v}$
and
$\overline {v}$
and
![]() $\overline {w}$
differ at only coordinate i, we have
$\overline {w}$
differ at only coordinate i, we have
![]() $v_i=u$
and
$v_i=u$
and
![]() $w_i\in F$
. We have
$w_i\in F$
. We have
 $$ \begin{align*} & |R^{F_u}(\overline{v})-R^{F_u}(\overline{w})| \\& \quad \leq |R^{F_u}(\overline{v})-R^{A_x}(\overline{v}')|+|R^{A_x}(\overline{v}')-R^{M}(\overline{w}')| +|R^{M}(\overline{w}')-R^M(\overline{w})| \\& \quad \leq K\displaystyle\frac{\epsilon}{2}+d^{A_x}_R(\overline{v}', \overline{w}')+d^M_R(\overline{w}',\overline{w}) \\& \quad \leq K\displaystyle\frac{\epsilon}{2}+K_{R,i}d^{A_x}(x, w_i')+\sum_{j=1}^n K_{R,j}d^M(w_j', w_j) \\& \quad \leq K_{R,i}d^{A_x}(x, w_i')+K_{R,i}\displaystyle\frac{\epsilon}{2}+NJK_{R,i}\frac{\epsilon_0}{2NJ} \\& \quad < K_{R,i}d^{F_u}(u, w_i). \end{align*} $$
$$ \begin{align*} & |R^{F_u}(\overline{v})-R^{F_u}(\overline{w})| \\& \quad \leq |R^{F_u}(\overline{v})-R^{A_x}(\overline{v}')|+|R^{A_x}(\overline{v}')-R^{M}(\overline{w}')| +|R^{M}(\overline{w}')-R^M(\overline{w})| \\& \quad \leq K\displaystyle\frac{\epsilon}{2}+d^{A_x}_R(\overline{v}', \overline{w}')+d^M_R(\overline{w}',\overline{w}) \\& \quad \leq K\displaystyle\frac{\epsilon}{2}+K_{R,i}d^{A_x}(x, w_i')+\sum_{j=1}^n K_{R,j}d^M(w_j', w_j) \\& \quad \leq K_{R,i}d^{A_x}(x, w_i')+K_{R,i}\displaystyle\frac{\epsilon}{2}+NJK_{R,i}\frac{\epsilon_0}{2NJ} \\& \quad < K_{R,i}d^{F_u}(u, w_i). \end{align*} $$
Now we have established (UCℒ
) for all
![]() $R\in \mathcal {L}$
in
$R\in \mathcal {L}$
in
![]() $F_u$
, we get that
$F_u$
, we get that
![]() $\mathcal {F}_u$
is indeed a one-point extension of
$\mathcal {F}_u$
is indeed a one-point extension of
![]() $\mathcal {F}$
as a continuous
$\mathcal {F}$
as a continuous
![]() $\mathcal {L}$
-structure.
$\mathcal {L}$
-structure.
By Theorem 3.9, the canonical amalgam of
![]() $\mathcal {F}_u$
and
$\mathcal {F}_u$
and
![]() $\mathcal {M}$
over
$\mathcal {M}$
over
![]() $\mathcal {F}$
gives us a one-point extension
$\mathcal {F}$
gives us a one-point extension
![]() $\mathcal {M}_u$
of
$\mathcal {M}_u$
of
![]() $\mathcal {M}$
. Hence
$\mathcal {M}$
. Hence
![]() $u\in E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
.
$u\in E(\mathcal {M},\omega )\cap E'(\mathcal {M})$
.
To complete the proof of the theorem, we claim that
![]() $d^E(x, u)<(NJ+1)\epsilon $
. For this, we note that for any
$d^E(x, u)<(NJ+1)\epsilon $
. For this, we note that for any
![]() $y\in M$
,
$y\in M$
,
and
Fix an arbitrary
![]() $y\in M$
. Suppose first
$y\in M$
. Suppose first
![]() $d^{M_u}(u, y)< d^{M_x}(x,y)$
, and let
$d^{M_u}(u, y)< d^{M_x}(x,y)$
, and let
![]() $d^{M_u}(u,y)=d^{F_u}(u, b_i)+d^M(b_i,y)$
. Then
$d^{M_u}(u,y)=d^{F_u}(u, b_i)+d^M(b_i,y)$
. Then
 $$ \begin{align*} & d^{M_x}(x, y)-d^{M_u}(u,y) \\& \quad \leq d^{A_x}(x, a_i)+d^M(a_i, y)-(d^{F_u}(u, b_i)+d^M(b_i, y)) \\&\quad \leq d^{A_x}(x, a_i)-d^{F_u}(u, b_i)+d^M(a_i, b_i) \\&\quad \leq \displaystyle\frac{\epsilon_0}{2NJ}-\displaystyle\frac{\epsilon}{2}<0, \end{align*} $$
$$ \begin{align*} & d^{M_x}(x, y)-d^{M_u}(u,y) \\& \quad \leq d^{A_x}(x, a_i)+d^M(a_i, y)-(d^{F_u}(u, b_i)+d^M(b_i, y)) \\&\quad \leq d^{A_x}(x, a_i)-d^{F_u}(u, b_i)+d^M(a_i, b_i) \\&\quad \leq \displaystyle\frac{\epsilon_0}{2NJ}-\displaystyle\frac{\epsilon}{2}<0, \end{align*} $$
contradicting our assumption. Hence we must have
![]() $d^{M_u}(u, y)\geq d^{M_x}(x, y)$
. Let
$d^{M_u}(u, y)\geq d^{M_x}(x, y)$
. Let
![]() $d^{M_x}(x,y)=d^{A_x}(x, a_i)+d^M(a_i, y)$
. Then
$d^{M_x}(x,y)=d^{A_x}(x, a_i)+d^M(a_i, y)$
. Then
 $$ \begin{align*} & d^{M_u}(u, y)-d^{M_x}(x, y) \\& \quad \leq d^{F_u}(u, b_i)+d^M(b_i,y)-(d^{A_x}(x, a_i)+d^M(a_i, y)) \\& \quad \leq d^{F_u}(u,b_i)-d^{A_x}(x, a_i)+d^M(a_i, b_i) \\& \quad \leq (3m+2)\epsilon_0+\displaystyle\frac{\epsilon}{2}+\frac{\epsilon_0}{2NJ}<\frac{5}{6}\epsilon. \end{align*} $$
$$ \begin{align*} & d^{M_u}(u, y)-d^{M_x}(x, y) \\& \quad \leq d^{F_u}(u, b_i)+d^M(b_i,y)-(d^{A_x}(x, a_i)+d^M(a_i, y)) \\& \quad \leq d^{F_u}(u,b_i)-d^{A_x}(x, a_i)+d^M(a_i, b_i) \\& \quad \leq (3m+2)\epsilon_0+\displaystyle\frac{\epsilon}{2}+\frac{\epsilon_0}{2NJ}<\frac{5}{6}\epsilon. \end{align*} $$
It follows that
![]() $\lambda (x, u)<\epsilon $
.
$\lambda (x, u)<\epsilon $
.
For any unary
![]() $R\in \mathcal {L}$
, we have
$R\in \mathcal {L}$
, we have
Thus
![]() $\mu (x, u)<\epsilon $
.
$\mu (x, u)<\epsilon $
.
To compute
![]() $\rho (x,u)$
, we fix an n-ary
$\rho (x,u)$
, we fix an n-ary
![]() $R\in \mathcal {L}$
for
$R\in \mathcal {L}$
for
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $\overline {v}\in M_u^n\setminus M^n$
. Since
$\overline {v}\in M_u^n\setminus M^n$
. Since
![]() $\mathcal {M}_u$
is the canonical amalgam of
$\mathcal {M}_u$
is the canonical amalgam of
![]() $\mathcal {F}_u$
and
$\mathcal {F}_u$
and
![]() $\mathcal {M}$
over
$\mathcal {M}$
over
![]() $\mathcal {F}$
, we have that
$\mathcal {F}$
, we have that
Similarly,
Suppose first
![]() $R^{M_u}(\overline {v}){\kern-1pt}\geq{\kern-1pt} R^{M_x}(\overline {v}(x|u))$
. If
$R^{M_u}(\overline {v}){\kern-1pt}\geq{\kern-1pt} R^{M_x}(\overline {v}(x|u))$
. If
![]() $R^{M_u}(\overline {v}){\kern-1pt}={\kern-1pt}0$
we must have
$R^{M_u}(\overline {v}){\kern-1pt}={\kern-1pt}0$
we must have
![]() ${R^{M_x}(\overline {v}(x|u)){\kern-1pt}={\kern-1pt}0}$
and there is nothing to prove. Assume
${R^{M_x}(\overline {v}(x|u)){\kern-1pt}={\kern-1pt}0}$
and there is nothing to prove. Assume
![]() $R^{M_u}(\overline {v})>0$
. Let
$R^{M_u}(\overline {v})>0$
. Let
![]() $\eta>0$
be arbitrary. Then for some
$\eta>0$
be arbitrary. Then for some
![]() $\overline {z}\in F_u^n\cup M^n$
,
$\overline {z}\in F_u^n\cup M^n$
,
Consider first the case
![]() $\overline {z}\in M^n$
. Then
$\overline {z}\in M^n$
. Then
 $$ \begin{align*} & R^{M_u}(\overline{v})-R^{M_x}(\overline{v}(x|u)) \\&\quad\leq R^{M_u}(\overline{z})-d^{M_u}_R(\overline{v},\overline{z})+\eta-(R^{M_x}(\overline{z})-d^{M_x}_R(\overline{v}(x|u), \overline{z})) \\&\quad\leq \|\overline{v}\|\lambda(u,x)+\eta. \end{align*} $$
$$ \begin{align*} & R^{M_u}(\overline{v})-R^{M_x}(\overline{v}(x|u)) \\&\quad\leq R^{M_u}(\overline{z})-d^{M_u}_R(\overline{v},\overline{z})+\eta-(R^{M_x}(\overline{z})-d^{M_x}_R(\overline{v}(x|u), \overline{z})) \\&\quad\leq \|\overline{v}\|\lambda(u,x)+\eta. \end{align*} $$
Since
![]() $\eta $
is arbitrary, we have
$\eta $
is arbitrary, we have
Next consider the case
![]() $\overline {z}\in F_u^n\setminus F^n$
. Then
$\overline {z}\in F_u^n\setminus F^n$
. Then
 $$ \begin{align*} & R^{M_u}(\overline{v})-R^{M_x}(\overline{v}(x|u)) \\&\quad\leq R^{M_u}(\overline{z})-d^{M_u}_R(\overline{v},\overline{z})+\eta-(R^{M_x}(\overline{z}')-d^{M_x}_R(\overline{v}(x|u), \overline{z}') \\&\quad= R^{M_u}(\overline{z})-R^{M_x}(\overline{z}')+(d^{M_x}_R(\overline{v}(x|u), \overline{z}')-d^{M_u}_R(\overline{v}, \overline{z}))+\eta \\& \quad\leq K\displaystyle\frac{\epsilon}{2}+NKJ \epsilon+\eta. \end{align*} $$
$$ \begin{align*} & R^{M_u}(\overline{v})-R^{M_x}(\overline{v}(x|u)) \\&\quad\leq R^{M_u}(\overline{z})-d^{M_u}_R(\overline{v},\overline{z})+\eta-(R^{M_x}(\overline{z}')-d^{M_x}_R(\overline{v}(x|u), \overline{z}') \\&\quad= R^{M_u}(\overline{z})-R^{M_x}(\overline{z}')+(d^{M_x}_R(\overline{v}(x|u), \overline{z}')-d^{M_u}_R(\overline{v}, \overline{z}))+\eta \\& \quad\leq K\displaystyle\frac{\epsilon}{2}+NKJ \epsilon+\eta. \end{align*} $$
The last inequality follows from the observation that there are four cases for the values of
![]() $v_i, z_i\in M_u$
:
$v_i, z_i\in M_u$
:
-
Case 1.
 $v_i=u$
and
$v_i=u$
and
 $z_i=u$
. Then
$z_i=u$
. Then
 $z_i'=x$
and
$z_i'=x$
and
 $v_i(x|u)=x$
. In this case
$v_i(x|u)=x$
. In this case
 $d^{M_x}(v_i(x|u), z_i')-d^{M_u}(v_i, z_i)=0$
.
$d^{M_x}(v_i(x|u), z_i')-d^{M_u}(v_i, z_i)=0$
. -
Case 2.
 $v_i\in M$
and
$v_i\in M$
and
 $z_i=b_j\in F$
. Then
$z_i=b_j\in F$
. Then
 $z_i'=a_j\in A$
and
$z_i'=a_j\in A$
and
 $v_i(x|u)=v_i$
. In this case
$v_i(x|u)=v_i$
. In this case  $$ \begin{align*}|d^{M_x}(v_i(x|u), z_i')-d^{M_u}(v_i,z_i)|\leq d^M(a_j, b_j)<\displaystyle\frac{\epsilon_0}{2NJ}<\epsilon.\end{align*} $$
$$ \begin{align*}|d^{M_x}(v_i(x|u), z_i')-d^{M_u}(v_i,z_i)|\leq d^M(a_j, b_j)<\displaystyle\frac{\epsilon_0}{2NJ}<\epsilon.\end{align*} $$
-
Case 3.
 $v_i=u$
and
$v_i=u$
and
 $z_i=b_j\in F$
. Then
$z_i=b_j\in F$
. Then
 $z_i'=a_j\in A$
and
$z_i'=a_j\in A$
and
 $v_i(x|u)=x$
. In this case
$v_i(x|u)=x$
. In this case  $$ \begin{align*} |d^{M_x}(v_i(x|u),z_i')-d^{M_u}(v_i, z_i)|&=|d^{M_x}(x, a_j)-d^{M_u}(u, b_j)| \\ &\leq (3m+2)\epsilon_0+\displaystyle\frac{\epsilon}{2}<\epsilon. \end{align*} $$
$$ \begin{align*} |d^{M_x}(v_i(x|u),z_i')-d^{M_u}(v_i, z_i)|&=|d^{M_x}(x, a_j)-d^{M_u}(u, b_j)| \\ &\leq (3m+2)\epsilon_0+\displaystyle\frac{\epsilon}{2}<\epsilon. \end{align*} $$
-
Case 4.
 $v_i\in M$
and
$v_i\in M$
and
 $z_i=u$
. Then
$z_i=u$
. Then
 $z_i'=x$
and
$z_i'=x$
and
 $v_i(x|u)=v_i$
. In this case
$v_i(x|u)=v_i$
. In this case  $$ \begin{align*} |d^{M_x}(v_i(x|u), z_i')-d^{M_u}(v_i,z_i)|&=|d^{M_x}(v_i, x)-d^{M_u}(v_i, u)| \\ &\leq \lambda(u,x)<\epsilon. \end{align*} $$
$$ \begin{align*} |d^{M_x}(v_i(x|u), z_i')-d^{M_u}(v_i,z_i)|&=|d^{M_x}(v_i, x)-d^{M_u}(v_i, u)| \\ &\leq \lambda(u,x)<\epsilon. \end{align*} $$
Since
![]() $\eta $
is arbitrary, we have
$\eta $
is arbitrary, we have
Since
![]() $\|\overline {v}\|\geq K$
, we have
$\|\overline {v}\|\geq K$
, we have
For
![]() $R^{M_u}(\overline {v})\leq R^{M_x}(\overline {v}(x|u))$
we get a similar estimate by a symmetric argument. Thus we have
$R^{M_u}(\overline {v})\leq R^{M_x}(\overline {v}(x|u))$
we get a similar estimate by a symmetric argument. Thus we have
![]() $\rho (x, u)<(NJ+1)\epsilon $
and
$\rho (x, u)<(NJ+1)\epsilon $
and
![]() $d^E(x,u)<(NJ+1)\epsilon $
.
$d^E(x,u)<(NJ+1)\epsilon $
.
4.3. Construction of the Urysohn structure
Given any proper continuous signature
![]() $\mathcal {L}$
and continuous
$\mathcal {L}$
and continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
, define by induction
$\mathcal {M}$
, define by induction
 $$ \begin{align*}\mathcal{M}_0&=\mathcal{M}\\ \mathcal{M}_{n+1}&= \mathcal{E}(\mathcal{M}_n,\omega),\end{align*} $$
$$ \begin{align*}\mathcal{M}_0&=\mathcal{M}\\ \mathcal{M}_{n+1}&= \mathcal{E}(\mathcal{M}_n,\omega),\end{align*} $$
and let
Then by Theorem 4.5, if
![]() $\mathcal {M}$
is separable, then so is
$\mathcal {M}$
is separable, then so is
![]() $\mathcal {M}_\omega $
. From the construction of
$\mathcal {M}_\omega $
. From the construction of
![]() $\mathcal {M}_\omega $
it is easy to see that it always has the Urysohn property.
$\mathcal {M}_\omega $
it is easy to see that it always has the Urysohn property.
By the properness of
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
![]() $\mathcal {M}_\omega $
has a unique completion
$\mathcal {M}_\omega $
has a unique completion
![]() $\bar {\mathcal {M}}_\omega $
which is a continuous
$\bar {\mathcal {M}}_\omega $
which is a continuous
![]() $\mathcal {L}$
-structure. We show that
$\mathcal {L}$
-structure. We show that
![]() $\bar {\mathcal {M}}_\omega $
still has the Urysohn property. For this we first note the following corollary of the proof of Theorem 4.5.
$\bar {\mathcal {M}}_\omega $
still has the Urysohn property. For this we first note the following corollary of the proof of Theorem 4.5.
Lemma 4.6. Let
![]() $\mathcal {L}$
be a proper continuous signature and let
$\mathcal {L}$
be a proper continuous signature and let
![]() $\mathcal {M}$
be a continuous
$\mathcal {M}$
be a continuous
![]() $\mathcal {L}$
-pre-structure. Suppose
$\mathcal {L}$
-pre-structure. Suppose
![]() $\mathcal {M}$
has the Urysohn property. Given any finite substructure
$\mathcal {M}$
has the Urysohn property. Given any finite substructure
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\bar {\mathcal {M}}$
, a one-point extension
$\bar {\mathcal {M}}$
, a one-point extension
![]() $\mathcal {A}_x$
of
$\mathcal {A}_x$
of
![]() $\mathcal {A}$
, and
$\mathcal {A}$
, and
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $u\in M$
such that
$u\in M$
such that
and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {y}\in A_x^n$
,
$\overline {y}\in A_x^n$
,
Proof Let
![]() $\mathcal {A}_x$
and
$\mathcal {A}_x$
and
![]() $\epsilon>0$
be given. Let N, K, J be defined as in the proof of Theorem 4.5. Suppose
$\epsilon>0$
be given. Let N, K, J be defined as in the proof of Theorem 4.5. Suppose
![]() $A=\{a_0,\dots , a_m\}\subseteq \bar {M}$
. Since M is dense in
$A=\{a_0,\dots , a_m\}\subseteq \bar {M}$
. Since M is dense in
![]() $\bar {M}$
, we get a finite subset
$\bar {M}$
, we get a finite subset
![]() $F=\{b_0,\dots , b_m\}\subseteq M$
such that
$F=\{b_0,\dots , b_m\}\subseteq M$
such that
for all
![]() $0\leq i\leq m$
. By the proof of Theorem 4.5, we obtain an one-point extension
$0\leq i\leq m$
. By the proof of Theorem 4.5, we obtain an one-point extension
![]() $\mathcal {F}_u$
of
$\mathcal {F}_u$
of
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
for all
![]() $a\in A$
where
$a\in A$
where
![]() $b=b_j$
if
$b=b_j$
if
![]() $a=a_j$
for
$a=a_j$
for
![]() $0\leq j\leq m$
, and for any n-ary
$0\leq j\leq m$
, and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {y}\in A^n_x$
,
$\overline {y}\in A^n_x$
,
where
![]() $\overline {y}'$
is defined as in the proof of Theorem 4.5.
$\overline {y}'$
is defined as in the proof of Theorem 4.5.
Since M has the Urysohn property, we may find such a
![]() $u\in M$
. Now for any
$u\in M$
. Now for any
![]() $a\in A$
, letting
$a\in A$
, letting
![]() $b\in F$
be defined as above, we have
$b\in F$
be defined as above, we have
 $$ \begin{align*} & |d^{A_x}(x, a)-d^{\bar{M}}(u,a)| \\&\quad \leq |d^{A_x}(x, a)-d^{F_u}(u, b)|+|d^{F_u}(u, b)-d^{\bar{M}}(u, a)| \\&\quad < \displaystyle\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon. \end{align*} $$
$$ \begin{align*} & |d^{A_x}(x, a)-d^{\bar{M}}(u,a)| \\&\quad \leq |d^{A_x}(x, a)-d^{F_u}(u, b)|+|d^{F_u}(u, b)-d^{\bar{M}}(u, a)| \\&\quad < \displaystyle\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon. \end{align*} $$
For n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {y}\in A_x^n$
,
$\overline {y}\in A_x^n$
,
 $$ \begin{align*}& |R^{A_x}(\overline{y})-R^{\bar{M}}(\overline{y}(u|x))| \\& \quad \leq |R^{A_x}(\overline{y})-R^{F_u}(\overline{y}')|+|R^{F_u}(\overline{y}')-R^{\bar{M}}(\overline{y}(u|x))| \\& \quad \leq \displaystyle\frac{\epsilon}{2}+d_R^{\bar{M}}(\overline{y}',\overline{y}(u|x)) \\& \quad \leq \displaystyle\frac{\epsilon}{2}+NKJ\frac{\epsilon}{2NKJ}=\epsilon.\\[-37pt] \end{align*} $$
$$ \begin{align*}& |R^{A_x}(\overline{y})-R^{\bar{M}}(\overline{y}(u|x))| \\& \quad \leq |R^{A_x}(\overline{y})-R^{F_u}(\overline{y}')|+|R^{F_u}(\overline{y}')-R^{\bar{M}}(\overline{y}(u|x))| \\& \quad \leq \displaystyle\frac{\epsilon}{2}+d_R^{\bar{M}}(\overline{y}',\overline{y}(u|x)) \\& \quad \leq \displaystyle\frac{\epsilon}{2}+NKJ\frac{\epsilon}{2NKJ}=\epsilon.\\[-37pt] \end{align*} $$
The following lemma is also obvious.
Lemma 4.7. Let
![]() $\mathcal {M}$
be a continuous
$\mathcal {M}$
be a continuous
![]() $\mathcal {L}$
-pre-structure, and
$\mathcal {L}$
-pre-structure, and
![]() $\mathcal {M}_x$
and
$\mathcal {M}_x$
and
![]() $\mathcal {M}_y$
be two nonisomorphic one-point extensions of
$\mathcal {M}_y$
be two nonisomorphic one-point extensions of
![]() $\mathcal {M}$
. Then
$\mathcal {M}$
. Then
![]() $\mathcal {M}$
has an extension
$\mathcal {M}$
has an extension
![]() $\mathcal {M}_{xy}$
with
$\mathcal {M}_{xy}$
with
![]() $M_{xy}=M\cup \{x, y\}$
such that
$M_{xy}=M\cup \{x, y\}$
such that
Proof Take
![]() $\mathcal {M}_{xy}$
to be the substructure of
$\mathcal {M}_{xy}$
to be the substructure of
![]() $\mathcal {E}(\mathcal {M})$
with domain
$\mathcal {E}(\mathcal {M})$
with domain
![]() $M_{xy}$
.
$M_{xy}$
.
Theorem 4.8. Let
![]() $\mathcal {L}$
be a proper continuous signature and let
$\mathcal {L}$
be a proper continuous signature and let
![]() $\mathcal {M}$
be a continuous
$\mathcal {M}$
be a continuous
![]() $\mathcal {L}$
-pre-structure. If
$\mathcal {L}$
-pre-structure. If
![]() $\mathcal {M}$
has the Urysohn property, then so does its completion
$\mathcal {M}$
has the Urysohn property, then so does its completion
![]() $\bar {\mathcal {M}}$
.
$\bar {\mathcal {M}}$
.
Proof Let
![]() $A\subseteq \bar {M}$
and
$A\subseteq \bar {M}$
and
![]() $\mathcal {A}_x$
be a one-point extension of
$\mathcal {A}_x$
be a one-point extension of
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
We define a sequence
![]() $(y_m)$
in M by induction on m. By Lemma 4.6 there is
$(y_m)$
in M by induction on m. By Lemma 4.6 there is
![]() $y_0\in M$
such that
$y_0\in M$
such that
for any unary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {z}\in A^n_x$
,
$\overline {z}\in A^n_x$
,
where K is defined as in the proof of Theorem 4.5. Let
![]() $B_0=A\cup \{y_0\}\subseteq \bar {M}$
. By Lemma 4.7 we obtain a one-point extension
$B_0=A\cup \{y_0\}\subseteq \bar {M}$
. By Lemma 4.7 we obtain a one-point extension
![]() $(\mathcal {B}_0)_x=\mathcal {A}_{xy_0}$
such that
$(\mathcal {B}_0)_x=\mathcal {A}_{xy_0}$
such that
In general, assume
![]() $y_m$
has been defined to satisfy the following inductive hypothesis: for
$y_m$
has been defined to satisfy the following inductive hypothesis: for
there is an one-point extension
![]() $(\mathcal {B}_m)_x$
of
$(\mathcal {B}_m)_x$
of
![]() $\mathcal {B}_m$
(obtained from Lemma 4.7) such that
$\mathcal {B}_m$
(obtained from Lemma 4.7) such that
By Lemma 4.6 there is
![]() $y_{m+1}\in M$
such that
$y_{m+1}\in M$
such that
for any unary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
 $$ \begin{align*}|R^{(B_m)_x}(x)-R^{\bar{M}}(y_{m+1})|<\mathfrak{u}_{R,1}\left(\displaystyle\frac{\delta}{2^{m+1}}\right),\end{align*} $$
$$ \begin{align*}|R^{(B_m)_x}(x)-R^{\bar{M}}(y_{m+1})|<\mathfrak{u}_{R,1}\left(\displaystyle\frac{\delta}{2^{m+1}}\right),\end{align*} $$
and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {z}\in (B_m)_x^n$
,
$\overline {z}\in (B_m)_x^n$
,
Now let
and
![]() $(\mathcal {B}_{m+1})_x$
be given by Lemma 4.7 such that
$(\mathcal {B}_{m+1})_x$
be given by Lemma 4.7 such that
The inductive step of the definition is complete, and the inductive hypothesis is maintained. Note that
 $$ \begin{align*} d^M(y_m, y_{m+1})&\leq d^{(B_m)_x}(x, y_{m})+d^{(B_{m+1})_x}(x, y_{m+1}) \\ &<\displaystyle\frac{\delta}{2^m}+\frac{\delta}{2^{m+1}}<\frac{\delta}{2^{m-1}}. \end{align*} $$
$$ \begin{align*} d^M(y_m, y_{m+1})&\leq d^{(B_m)_x}(x, y_{m})+d^{(B_{m+1})_x}(x, y_{m+1}) \\ &<\displaystyle\frac{\delta}{2^m}+\frac{\delta}{2^{m+1}}<\frac{\delta}{2^{m-1}}. \end{align*} $$
Thus
![]() $(y_m)$
is a
$(y_m)$
is a
![]() $d^M$
-Cauchy sequence in M. Let
$d^M$
-Cauchy sequence in M. Let
![]() $y=\lim _m y_m\in \bar {M}$
. Then for any
$y=\lim _m y_m\in \bar {M}$
. Then for any
![]() $a\in A$
, since
$a\in A$
, since
letting
![]() $m\to \infty $
, we get that
$m\to \infty $
, we get that
For any unary
![]() $R\in \mathcal {L}$
, we have
$R\in \mathcal {L}$
, we have
 $$ \begin{align*}|R^{A_x}(x)-R^{\bar{M}}(y_m)|<\mathfrak{u}_{R,1} \left(\displaystyle\frac{\delta}{2^{m}}\right).\end{align*} $$
$$ \begin{align*}|R^{A_x}(x)-R^{\bar{M}}(y_m)|<\mathfrak{u}_{R,1} \left(\displaystyle\frac{\delta}{2^{m}}\right).\end{align*} $$
Since
![]() $\mathfrak {u}$
is continuous at
$\mathfrak {u}$
is continuous at
![]() $0$
, by letting
$0$
, by letting
![]() $m\to \infty $
we get
$m\to \infty $
we get
For any n-ary
![]() $\mathcal {R}\in \mathcal {L}$
and
$\mathcal {R}\in \mathcal {L}$
and
![]() $\overline {z}\in A_x^n$
,
$\overline {z}\in A_x^n$
,
Letting
![]() $m\to \infty $
, we obtain
$m\to \infty $
, we obtain
This shows that
![]() $\mathcal {A}_x$
and
$\mathcal {A}_x$
and
![]() $\mathcal {A}_y$
are isomorphic, and in particular there is an isomorphic embedding
$\mathcal {A}_y$
are isomorphic, and in particular there is an isomorphic embedding
![]() $\varphi : \mathcal {A}_x\to \mathcal {\bar {M}}$
with
$\varphi : \mathcal {A}_x\to \mathcal {\bar {M}}$
with
![]() $\varphi (a)=a$
for all
$\varphi (a)=a$
for all
![]() $a\in A$
.
$a\in A$
.
Thus we have shown that for any proper continuous signature
![]() $\mathcal {L}$
and continuous
$\mathcal {L}$
and continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\bar {\mathcal {M}}_\omega $
is a continuous
$\bar {\mathcal {M}}_\omega $
is a continuous
![]() $\mathcal {L}$
-structure with the Urysohn property. Since any two separable continuous
$\mathcal {L}$
-structure with the Urysohn property. Since any two separable continuous
![]() $\mathcal {L}$
-structures with the Urysohn property are isomorphic, by the above procedure we obtain this unique separable continuous
$\mathcal {L}$
-structures with the Urysohn property are isomorphic, by the above procedure we obtain this unique separable continuous
![]() $\mathcal {L}$
-structure as
$\mathcal {L}$
-structure as
![]() $\bar {\mathcal {M}}_\omega $
for any separable continuous
$\bar {\mathcal {M}}_\omega $
for any separable continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
We denote this unique separable continuous
![]() $\mathcal {L}$
-structure with the Urysohn property as
$\mathcal {L}$
-structure with the Urysohn property as
![]() $\mathbb {U}_{\mathcal {L}}$
.
$\mathbb {U}_{\mathcal {L}}$
.
4.4. Properties of the Urysohn structures
In the preceding subsection we showed one direction of Theorem 1.1(i), i.e., if
![]() $\mathcal {L}$
is a proper continuous signature, then there exists a (separable) continuous
$\mathcal {L}$
is a proper continuous signature, then there exists a (separable) continuous
![]() $\mathcal {L}$
-structure with the Urysohn property. In the following we prove the rest of Theorem 1.1.
$\mathcal {L}$
-structure with the Urysohn property. In the following we prove the rest of Theorem 1.1.
We first show that if
![]() $\mathcal {L}$
is semiproper, then for any continuous
$\mathcal {L}$
is semiproper, then for any continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {M}_\omega $
is a continuous
$\mathcal {M}_\omega $
is a continuous
![]() $\mathcal {L}$
-pre-structure with the Urysohn property. Note that
$\mathcal {L}$
-pre-structure with the Urysohn property. Note that
![]() $\mathcal {E}(\mathcal {M}, \omega )$
is not necessarily complete or even has a completion. We also do not need to address the separability of
$\mathcal {E}(\mathcal {M}, \omega )$
is not necessarily complete or even has a completion. We also do not need to address the separability of
![]() $\mathcal {M}_\omega $
. The proof requires only an observation that the upper semicontinuity is not used in the construction of
$\mathcal {M}_\omega $
. The proof requires only an observation that the upper semicontinuity is not used in the construction of
![]() $\mathcal {M}_\omega $
.
$\mathcal {M}_\omega $
.
Theorem 4.9. Let
![]() $\mathcal {L}$
be a semiproper continuous signature and
$\mathcal {L}$
be a semiproper continuous signature and
![]() $\mathcal {M}$
be a continuous
$\mathcal {M}$
be a continuous
![]() $\mathcal {L}$
-pre-structure. Then
$\mathcal {L}$
-pre-structure. Then
![]() $\mathcal {M}_\omega $
is a continuous
$\mathcal {M}_\omega $
is a continuous
![]() $\mathcal {L}$
-pre-structure with the Urysohn property.
$\mathcal {L}$
-pre-structure with the Urysohn property.
Proof We first claim that for any continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
and finite subsets
$\mathcal {M}$
and finite subsets
![]() $F\subseteq G$
of M, if the one-point extension
$F\subseteq G$
of M, if the one-point extension
![]() $\mathcal {M}_x$
has support F, then it also has support G. It is easy to verify that for any
$\mathcal {M}_x$
has support F, then it also has support G. It is easy to verify that for any
![]() $y\in M$
,
$y\in M$
,
If
![]() $R\in \mathcal {L}$
is n-ary, where
$R\in \mathcal {L}$
is n-ary, where
![]() $n\geq 2$
, and
$n\geq 2$
, and
![]() $\bar {u}\in M^n_x$
, then
$\bar {u}\in M^n_x$
, then
 $$ \begin{align*} R^{M_x}(\bar{u})&=\max\{0, \sup\{R^{M_x}(\bar{v})-d^{M_x}_R(\bar{u}, \bar{v}): \bar{v}\in M^n\cup F^n_x\}\}\\ &\leq\max\{0, \sup\{R^{M_x}(\bar{v})-d^{M_x}_R(\bar{u}, \bar{v}): \bar{v}\in M^n\cup G^n_x\}\}. \end{align*} $$
$$ \begin{align*} R^{M_x}(\bar{u})&=\max\{0, \sup\{R^{M_x}(\bar{v})-d^{M_x}_R(\bar{u}, \bar{v}): \bar{v}\in M^n\cup F^n_x\}\}\\ &\leq\max\{0, \sup\{R^{M_x}(\bar{v})-d^{M_x}_R(\bar{u}, \bar{v}): \bar{v}\in M^n\cup G^n_x\}\}. \end{align*} $$
On the other hand, if
![]() $\bar {v}\in M^n\cup G^n_x$
,
$\bar {v}\in M^n\cup G^n_x$
,
 $$ \begin{align*} R^{M_x}(\bar{v})-d^{M_x}_R(\bar{u}, \bar{v})&\leq\sup\{R^{M_x}(\bar{w})-d^{M_x}_R(\bar{v}, \bar{w})-d^{M_x}_R(\bar{u}, \bar{v}): \bar{w}\in M^n\cup F^n_x\}\\ &\leq\sup\{R^{M_x}(\bar{w})-d^{M_x}_R(\bar{u}, \bar{w}): \bar{w}\in M^n\cup F^n_x\}. \end{align*} $$
$$ \begin{align*} R^{M_x}(\bar{v})-d^{M_x}_R(\bar{u}, \bar{v})&\leq\sup\{R^{M_x}(\bar{w})-d^{M_x}_R(\bar{v}, \bar{w})-d^{M_x}_R(\bar{u}, \bar{v}): \bar{w}\in M^n\cup F^n_x\}\\ &\leq\sup\{R^{M_x}(\bar{w})-d^{M_x}_R(\bar{u}, \bar{w}): \bar{w}\in M^n\cup F^n_x\}. \end{align*} $$
So we have
as required.
To complete the proof, it suffices to show that
![]() $\mathcal {E}(\mathcal {M}, \omega )$
is a continuous
$\mathcal {E}(\mathcal {M}, \omega )$
is a continuous
![]() $\mathcal {L}$
-pre-structure, since
$\mathcal {L}$
-pre-structure, since
![]() $\mathcal {M}_\omega $
would be easily defined from iterating the definition of
$\mathcal {M}_\omega $
would be easily defined from iterating the definition of
![]() $\mathcal {E}(\mathcal {M},\omega )$
, and
$\mathcal {E}(\mathcal {M},\omega )$
, and
![]() $\mathcal {M}_\omega $
would have the Urysohn property by the construction. For this, we only observe that Lemmas 4.3 and 4.4 can be proved for
$\mathcal {M}_\omega $
would have the Urysohn property by the construction. For this, we only observe that Lemmas 4.3 and 4.4 can be proved for
![]() $\mathcal {E}(\mathcal {M},\omega )$
without using upper semicontinuity. For Lemma 4.3, only note that the use of Lemma 2.3 to obtain subadditivity of
$\mathcal {E}(\mathcal {M},\omega )$
without using upper semicontinuity. For Lemma 4.3, only note that the use of Lemma 2.3 to obtain subadditivity of
![]() $\mathfrak {u}^*_{R,1}$
does not require upper semicontinuity of
$\mathfrak {u}^*_{R,1}$
does not require upper semicontinuity of
![]() $\mathfrak {u}_{R,1}$
. For Lemma 4.4, the use of Lemma 2.3(3) in its proof does require upper semicontinuity. Below we provide an alternative proof of the relevant part for
$\mathfrak {u}_{R,1}$
. For Lemma 4.4, the use of Lemma 2.3(3) in its proof does require upper semicontinuity. Below we provide an alternative proof of the relevant part for
![]() $\mathcal {E}(\mathcal {M},\omega )$
without using upper semicontinuity.
$\mathcal {E}(\mathcal {M},\omega )$
without using upper semicontinuity.
Let
![]() $R\in \mathcal {L}$
be unary and
$R\in \mathcal {L}$
be unary and
![]() $x,y\in E'(\mathcal {M},\omega )$
, we need to show
$x,y\in E'(\mathcal {M},\omega )$
, we need to show
Suppose
![]() $\mathcal {M}_x$
has finite support
$\mathcal {M}_x$
has finite support
![]() $F\subseteq M$
and
$F\subseteq M$
and
![]() $\mathcal {M}_y$
has finite support
$\mathcal {M}_y$
has finite support
![]() $G\subseteq M$
. Then by the above claim both
$G\subseteq M$
. Then by the above claim both
![]() $\mathcal {M}_x$
and
$\mathcal {M}_x$
and
![]() $\mathcal {M}_y$
have finite support
$\mathcal {M}_y$
have finite support
![]() $H=F\cup G$
. It follows that
$H=F\cup G$
. It follows that
By the superadditivity of
![]() $\mathfrak {u}_{R,1}$
, we have that for any
$\mathfrak {u}_{R,1}$
, we have that for any
![]() $z\in H$
,
$z\in H$
,
 $$ \begin{align*} |R^{M_x}(x)-R^{M_y}(y)|&= |R^{H_x}(x)-R^{H_y}(y)| \\ &\leq |R^{H_x}(x)-R^H(z)|+|R^H(z)-R^{H_y}(y)| \\ &\leq \mathfrak{u}_{R,1}(d^{H_x}(x,z))+\mathfrak{u}_{R,1}(d^{H_y}(z,y)) \\ &\leq \mathfrak{u}_{R,1}(d^{H_x}(x,z)+d^{H_y}(z,y)).\end{align*} $$
$$ \begin{align*} |R^{M_x}(x)-R^{M_y}(y)|&= |R^{H_x}(x)-R^{H_y}(y)| \\ &\leq |R^{H_x}(x)-R^H(z)|+|R^H(z)-R^{H_y}(y)| \\ &\leq \mathfrak{u}_{R,1}(d^{H_x}(x,z))+\mathfrak{u}_{R,1}(d^{H_y}(z,y)) \\ &\leq \mathfrak{u}_{R,1}(d^{H_x}(x,z)+d^{H_y}(z,y)).\end{align*} $$
The required inequality follows from the monotonicity of
![]() $\mathfrak {u}_{R,1}$
because H is finite.
$\mathfrak {u}_{R,1}$
because H is finite.
Theorem 4.10. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing.
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are nondecreasing.
-
(1) If there exists a continuous
 $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
 $\mathcal {U}$
with the Urysohn property, then
$\mathcal {U}$
with the Urysohn property, then
 $\mathcal {L}$
is semiproper.
$\mathcal {L}$
is semiproper. -
(2) If there exists a (separable) continuous
 $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
 $\mathcal {U}$
with the Urysohn property, then
$\mathcal {U}$
with the Urysohn property, then
 $\mathcal {L}$
is proper.
$\mathcal {L}$
is proper.
Proof (1) By Theorem 3.8 it suffices to show that the AP holds for
![]() ${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
. Let
${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
. Let
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {Q}$
be finite continuous
$\mathcal {Q}$
be finite continuous
![]() $\mathcal {L}$
-structures with isomorphic embeddings
$\mathcal {L}$
-structures with isomorphic embeddings
![]() $\varphi : M\to P$
and
$\varphi : M\to P$
and
![]() $\psi : M\to Q$
. By the Urysohn property of
$\psi : M\to Q$
. By the Urysohn property of
![]() $\mathcal {U}$
, we can find a substructure
$\mathcal {U}$
, we can find a substructure
![]() $\mathcal {P}'$
of
$\mathcal {P}'$
of
![]() $\mathcal {U}$
that is isomorphic to
$\mathcal {U}$
that is isomorphic to
![]() $\mathcal {P}$
. Let
$\mathcal {P}$
. Let
![]() $i:P\to P'$
be an isomorphism. Let
$i:P\to P'$
be an isomorphism. Let
![]() $M'=i\circ \varphi (M)\subseteq U$
. Then
$M'=i\circ \varphi (M)\subseteq U$
. Then
![]() $i\circ \varphi $
is an isomorphism between
$i\circ \varphi $
is an isomorphism between
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {M}'$
as a substructure of
$\mathcal {M}'$
as a substructure of
![]() $\mathcal {U}$
(or
$\mathcal {U}$
(or
![]() $\mathcal {P}'$
). Let
$\mathcal {P}'$
). Let
![]() $e:\psi (M)\to M'$
be
$e:\psi (M)\to M'$
be
![]() $i\circ \varphi \circ \psi ^{-1}$
. Then e is an isomorphism, and we have
$i\circ \varphi \circ \psi ^{-1}$
. Then e is an isomorphism, and we have
![]() $i\circ \varphi =e\circ \psi $
.
$i\circ \varphi =e\circ \psi $
.
By the Urysohn property of
![]() $\mathcal {U}$
we can find an extension
$\mathcal {U}$
we can find an extension
![]() $\mathcal {Q}'$
of
$\mathcal {Q}'$
of
![]() $\mathcal {M}'$
with
$\mathcal {M}'$
with
![]() ${Q'\subseteq U}$
such that
${Q'\subseteq U}$
such that
![]() $\mathcal {Q}'$
is isomorphic to
$\mathcal {Q}'$
is isomorphic to
![]() $\mathcal {Q}$
, and letting
$\mathcal {Q}$
, and letting
![]() $j: Q\to Q'$
be the isomorphism, we have
$j: Q\to Q'$
be the isomorphism, we have
![]() $j\,{\!\upharpoonright \!}\,\, \psi (M)=e$
. Now let
$j\,{\!\upharpoonright \!}\,\, \psi (M)=e$
. Now let
![]() $N=P'\cup Q'\subseteq U$
. Then
$N=P'\cup Q'\subseteq U$
. Then
![]() $\mathcal {N}$
is a substructure of U,
$\mathcal {N}$
is a substructure of U,
![]() $i: P\to N$
is an isomorphic embedding from
$i: P\to N$
is an isomorphic embedding from
![]() $\mathcal {P}$
into
$\mathcal {P}$
into
![]() $\mathcal {N}$
, and
$\mathcal {N}$
, and
![]() $j: P\to N$
is an isomorphic embedding from
$j: P\to N$
is an isomorphic embedding from
![]() $\mathcal {Q}$
into
$\mathcal {Q}$
into
![]() $\mathcal {N}$
. By our construction,
$\mathcal {N}$
. By our construction,
![]() $i\circ \varphi =j\circ \psi $
. Thus
$i\circ \varphi =j\circ \psi $
. Thus
![]() $\mathcal {N}$
is an amalgam of
$\mathcal {N}$
is an amalgam of
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $\mathcal {Q}$
over
$\mathcal {Q}$
over
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
(2) Assume that
![]() $\mathcal {U}$
is a continuous
$\mathcal {U}$
is a continuous
![]() $\mathcal {L}$
-structure with the Urysohn property. By (1),
$\mathcal {L}$
-structure with the Urysohn property. By (1),
![]() $\mathcal {L}$
is semiproper. It remains to show that given any unary
$\mathcal {L}$
is semiproper. It remains to show that given any unary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $\mathfrak {u}_{R, 1}$
is upper semicontinuous on
$\mathfrak {u}_{R, 1}$
is upper semicontinuous on
![]() $I_{R, 1}$
. Let
$I_{R, 1}$
. Let
![]() $I^\circ _{R, 1}$
be the interior of
$I^\circ _{R, 1}$
be the interior of
![]() $I_{R, 1}$
and assume
$I_{R, 1}$
and assume
![]() $a\in I^\circ _{R, 1}$
. Since
$a\in I^\circ _{R, 1}$
. Since
![]() $\mathcal {U}$
has the Urysohn property, there is a countable substructure
$\mathcal {U}$
has the Urysohn property, there is a countable substructure
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {U}$
where:
$\mathcal {U}$
where:
-
•
 $M=\{x_n\}_{n\geq 1}\cup \{y\}$
,
$M=\{x_n\}_{n\geq 1}\cup \{y\}$
, -
• for all
 $m, n\geq 1$
,
$m, n\geq 1$
,
 $d^M(x_n,y)=a+2^{-n}$
,
$d^M(x_n,y)=a+2^{-n}$
,
 $d^M(x_m, x_n)=|2^{-m}-2^{-n}|$
,
$d^M(x_m, x_n)=|2^{-m}-2^{-n}|$
, -
•
 $R^M(y)=\lim _{\delta \rightarrow 0^+}\mathfrak {u}_{R, 1}(a+\delta )<1$
,
$R^M(y)=\lim _{\delta \rightarrow 0^+}\mathfrak {u}_{R, 1}(a+\delta )<1$
,
 $R^M(x_n)=0$
for all
$R^M(x_n)=0$
for all
 $n\geq 1$
, and
$n\geq 1$
, and -
• for all other
 $R'\in \mathcal {L}$
,
$R'\in \mathcal {L}$
,
 ${R'}^M$
is identically
${R'}^M$
is identically
 $0$
.
$0$
.
Then by the completeness of
![]() $\mathcal {U}$
, there is
$\mathcal {U}$
, there is
![]() $z\in \mathcal {U}$
such that
$z\in \mathcal {U}$
such that
![]() $d^U(y, z)=a$
and
$d^U(y, z)=a$
and
![]() ${R^U(z)=0}$
, which implies that
${R^U(z)=0}$
, which implies that
In case
![]() $\mathcal {L}$
is proper, one naturally wonders whether the metric space underlying
$\mathcal {L}$
is proper, one naturally wonders whether the metric space underlying
![]() $\mathbb {U}_{\mathcal {L}}$
is isometric to the universal Urysohn metric space
$\mathbb {U}_{\mathcal {L}}$
is isometric to the universal Urysohn metric space
![]() $\mathbb {U}$
. The answer is not always.
$\mathbb {U}$
. The answer is not always.
Definition 4.11. A continuous signature
![]() $\mathcal {L}$
is Lipschitz if
$\mathcal {L}$
is Lipschitz if
![]() $\mathcal {L}$
consists of only finitely many relation symbols and for each n-ary
$\mathcal {L}$
consists of only finitely many relation symbols and for each n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $I_{R,i}$
is bounded and there is
$I_{R,i}$
is bounded and there is
![]() $K_{R,i}>0$
such that
$K_{R,i}>0$
such that
![]() $\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
$\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
![]() $r\in I_{r,i}$
.
$r\in I_{r,i}$
.
Any Lipschitz continuous signature is proper. If
![]() $\mathcal {L}$
does not contain any unary relation symbols, then
$\mathcal {L}$
does not contain any unary relation symbols, then
![]() $\mathcal {L}$
is proper iff it is Lipschitz.
$\mathcal {L}$
is proper iff it is Lipschitz.
Theorem 4.12. Let
![]() $\mathcal {L}$
be a proper continuous signature. Then the following are equivalent:
$\mathcal {L}$
be a proper continuous signature. Then the following are equivalent:
-
(i)
 $\mathcal {L}$
is Lipschitz.
$\mathcal {L}$
is Lipschitz. -
(ii) The metric space underlying
 $\mathbb {U}_{\mathcal {L}}$
is isometric to
$\mathbb {U}_{\mathcal {L}}$
is isometric to
 $\mathbb {U}$
.
$\mathbb {U}$
.
Proof For (i)
![]() $\Rightarrow $
(ii) let
$\Rightarrow $
(ii) let
![]() $A\subseteq \mathbb {U}_{\mathcal {L}}$
be finite and
$A\subseteq \mathbb {U}_{\mathcal {L}}$
be finite and
![]() $A_x$
be a metric space which is a one-point extension of A as a metric space. It suffices to show that x can be realized as a point in
$A_x$
be a metric space which is a one-point extension of A as a metric space. It suffices to show that x can be realized as a point in
![]() $\mathbb {U}_{\mathcal {L}}$
. For this we only need to make a continuous
$\mathbb {U}_{\mathcal {L}}$
. For this we only need to make a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {A}_x$
as a one-point extension of the substructure
$\mathcal {A}_x$
as a one-point extension of the substructure
![]() $\mathcal {A}$
. Observe that for any n-ary
$\mathcal {A}$
. Observe that for any n-ary
![]() $R\in \mathcal {L}$
, since
$R\in \mathcal {L}$
, since
![]() $\mathcal {L}$
is Lipschitz, we have that for any metric space
$\mathcal {L}$
is Lipschitz, we have that for any metric space
![]() $(X, d^X)$
and
$(X, d^X)$
and
![]() $\overline {u}=(u_1,\dots , u_n), \overline {v}=(v_1,\dots , v_n)\in X^n$
,
$\overline {u}=(u_1,\dots , u_n), \overline {v}=(v_1,\dots , v_n)\in X^n$
,
 $$ \begin{align*}d^X_R(\overline{u},\overline{v})=\displaystyle\sum_{i=1}^n K_id^X(u_i, v_i).\end{align*} $$
$$ \begin{align*}d^X_R(\overline{u},\overline{v})=\displaystyle\sum_{i=1}^n K_id^X(u_i, v_i).\end{align*} $$
Now for any n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^A$
is defined on
$R^A$
is defined on
![]() $A^n$
and is
$A^n$
and is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $d^A_R$
by Lemma 3.5. It follows that
$d^A_R$
by Lemma 3.5. It follows that
![]() $R^{A_x}$
is partially defined on
$R^{A_x}$
is partially defined on
![]() ${\mathrm {dom}}(R^{A_x})=A^n$
and is
${\mathrm {dom}}(R^{A_x})=A^n$
and is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $d^{A_x}_R$
. Thus by Lemma 3.7 we can define
$d^{A_x}_R$
. Thus by Lemma 3.7 we can define
![]() $R^{A_x}$
on
$R^{A_x}$
on
![]() $A_x^n$
so that
$A_x^n$
so that
![]() $\mathcal {A}_x$
is an extension of
$\mathcal {A}_x$
is an extension of
![]() $\mathcal {A}$
. By the Urysohn property of
$\mathcal {A}$
. By the Urysohn property of
![]() $\mathbb {U}_{\mathcal {L}}$
, x can now be realized as a point in
$\mathbb {U}_{\mathcal {L}}$
, x can now be realized as a point in
![]() $\mathbb {U}_{\mathcal {L}}$
as desired.
$\mathbb {U}_{\mathcal {L}}$
as desired.
For (ii)
![]() $\Rightarrow $
(i) assume
$\Rightarrow $
(i) assume
![]() $\mathcal {L}$
is proper but not Lipschitz. Then for some unary
$\mathcal {L}$
is proper but not Lipschitz. Then for some unary
![]() $R\in \mathcal {L}$
we have
$R\in \mathcal {L}$
we have
![]() $r_1, r_2>0$
with
$r_1, r_2>0$
with
![]() $r_1+r_2\in I_{R,1}$
and
$r_1+r_2\in I_{R,1}$
and
Now consider the continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
defined as follows.
$\mathcal {M}$
defined as follows.
and for any other
![]() $R'\in \mathcal {L}$
,
$R'\in \mathcal {L}$
,
![]() ${R'}^M$
is identically
${R'}^M$
is identically
![]() $0$
. Let
$0$
. Let
![]() $\mathcal {A}$
be a substructure of
$\mathcal {A}$
be a substructure of
![]() $\mathbb {U}_{\mathcal {L}}$
that is isomorphic to
$\mathbb {U}_{\mathcal {L}}$
that is isomorphic to
![]() $\mathcal {M}$
. Suppose
$\mathcal {M}$
. Suppose
![]() $A=\{x, y\}\subseteq \mathbb {U}_{\mathcal {L}}$
where
$A=\{x, y\}\subseteq \mathbb {U}_{\mathcal {L}}$
where
![]() $d^U(x,y)=r_1+r_2$
,
$d^U(x,y)=r_1+r_2$
,
![]() $R^U(x)=0$
and
$R^U(x)=0$
and
![]() $R^U(y)=\mathfrak {u}_{R,1}(r_1+r_2)$
. Now consider a metric one-point extension of
$R^U(y)=\mathfrak {u}_{R,1}(r_1+r_2)$
. Now consider a metric one-point extension of
![]() $(A, d^A)$
with an extra point z such that
$(A, d^A)$
with an extra point z such that
Assume toward a contradiction that
![]() $\mathbb {U}_{\mathcal {L}}$
is isometric to
$\mathbb {U}_{\mathcal {L}}$
is isometric to
![]() $\mathbb {U}$
. Then there is such a
$\mathbb {U}$
. Then there is such a
![]() $z\in \mathbb {U}_{\mathcal {L}}$
. Then
$z\in \mathbb {U}_{\mathcal {L}}$
. Then
 $$ \begin{align*}\mathfrak{u}_{R,1}(r_1+r_2)=|R^U(x)-R^U(y)|&\leq |R^U(x)-R^U(z)|+|R^U(z)-R^U(y)| \\ &\leq \mathfrak{u}_{R,1}(r_1)+\mathfrak{u}_{R,2}(r_2), \end{align*} $$
$$ \begin{align*}\mathfrak{u}_{R,1}(r_1+r_2)=|R^U(x)-R^U(y)|&\leq |R^U(x)-R^U(z)|+|R^U(z)-R^U(y)| \\ &\leq \mathfrak{u}_{R,1}(r_1)+\mathfrak{u}_{R,2}(r_2), \end{align*} $$
contradicting our assumption.
When
![]() $\mathcal {L}$
is proper but not Lipschitz, we can decompose
$\mathcal {L}$
is proper but not Lipschitz, we can decompose
![]() $\mathbb {U}_{\mathcal {L}}$
into continuum many substructures each of which has an isometric copy of
$\mathbb {U}_{\mathcal {L}}$
into continuum many substructures each of which has an isometric copy of
![]() $\mathbb {U}$
as its underlying metric space. The parameter space is
$\mathbb {U}$
as its underlying metric space. The parameter space is
![]() $[0,1]^k$
for some finite k. In fact, let
$[0,1]^k$
for some finite k. In fact, let
![]() $R_1,\dots , R_k$
be all the unary relation symbols in
$R_1,\dots , R_k$
be all the unary relation symbols in
![]() $\mathcal {L}$
whose associated moduli of continuity is not Lipschitz. For each
$\mathcal {L}$
whose associated moduli of continuity is not Lipschitz. For each
![]() $\overline {p}=(p_1,\dots , p_k)\in [0,1]^k$
, let
$\overline {p}=(p_1,\dots , p_k)\in [0,1]^k$
, let
Then for each
![]() $\overline {p}\in [0,1]^k$
, the metric space underlying each
$\overline {p}\in [0,1]^k$
, the metric space underlying each
![]() $\mathbb {U}_{\mathcal {L}, \overline {p}}$
is isometric to
$\mathbb {U}_{\mathcal {L}, \overline {p}}$
is isometric to
![]() $\mathbb {U}$
.
$\mathbb {U}$
.
Let
![]() $\mathcal {L}$
be a proper continuous signature. For any separable continuous
$\mathcal {L}$
be a proper continuous signature. For any separable continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
, equip
$\mathcal {M}$
, equip
![]() ${\mathrm {Aut}}(\mathcal {M})$
with the pointwise convergence topology. Then
${\mathrm {Aut}}(\mathcal {M})$
with the pointwise convergence topology. Then
![]() ${\mathrm { Aut}}(\mathcal {M})$
becomes a Polish group.
${\mathrm { Aut}}(\mathcal {M})$
becomes a Polish group.
It follows easily from Uspenskij’s method [Reference Uspenskij19] and our construction that
![]() ${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
is a universal Polish group.
${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
is a universal Polish group.
5. Fraïssé classes of finite continuous structures
In this section we consider some classes of finite continuous
![]() $\mathcal {L}$
-structures for semiproper
$\mathcal {L}$
-structures for semiproper
![]() $\mathcal {L}$
and show that they are Fraïssé classes. In particular, we construct the rational Urysohn
$\mathcal {L}$
and show that they are Fraïssé classes. In particular, we construct the rational Urysohn
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathbb {QU}_{\mathcal {L}}$
and show that its completion is isomorphic to
$\mathbb {QU}_{\mathcal {L}}$
and show that its completion is isomorphic to
![]() $\mathbb {U}_{\mathcal {L}}$
when
$\mathbb {U}_{\mathcal {L}}$
when
![]() $\mathcal {L}$
is proper.
$\mathcal {L}$
is proper.
Definition 5.1. Let
![]() $\mathcal {L}$
be a continuous signature. Let
$\mathcal {L}$
be a continuous signature. Let
![]() $\Delta \subseteq \mathbb {R}^+$
and
$\Delta \subseteq \mathbb {R}^+$
and
![]() $V\subseteq [0,1]$
.
$V\subseteq [0,1]$
.
-
(i) We call
 $\Delta $
a distance value set if for all
$\Delta $
a distance value set if for all
 $a, b\in \Delta $
,
$a, b\in \Delta $
,  $$ \begin{align*}\min\{a+b, \sup(\Delta)\}\in \Delta.\end{align*} $$
$$ \begin{align*}\min\{a+b, \sup(\Delta)\}\in \Delta.\end{align*} $$
-
(ii) We call the pair
 $(\Delta , V)$
a good value pair for
$(\Delta , V)$
a good value pair for
 $\mathcal {L}$
if:
$\mathcal {L}$
if:-
•
 $\Delta $
is a distance value set,
$\Delta $
is a distance value set, -
• if
 $\Delta $
is bounded, then for any n-ary
$\Delta $
is bounded, then for any n-ary
 $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
 $1\leq i\leq n$
,
$1\leq i\leq n$
,
 $\mathfrak {u}_{R,i}(\sup (\Delta ))\geq 1$
,
$\mathfrak {u}_{R,i}(\sup (\Delta ))\geq 1$
, -
•
 $0\in V$
, and
$0\in V$
, and -
• for any
 $v\in V$
, any
$v\in V$
, any
 $\delta \in \Delta $
, any n-ary
$\delta \in \Delta $
, any n-ary
 $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
 $1\leq i\leq n$
, if
$1\leq i\leq n$
, if
 $v>\mathfrak {u}_{R,i}(\delta )$
, then
$v>\mathfrak {u}_{R,i}(\delta )$
, then
 $v-\mathfrak {u}_{R,i}(\delta )\in V$
.
$v-\mathfrak {u}_{R,i}(\delta )\in V$
.
-
-
(iii) We say that
 $(\Delta , V)$
is finite (countable, respectively) if both
$(\Delta , V)$
is finite (countable, respectively) if both
 $\Delta $
and V are finite (countable, respectively).
$\Delta $
and V are finite (countable, respectively).
Definition 5.2. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {M}$
a continuous
$\mathcal {M}$
a continuous
![]() $\mathcal {L}$
-pre-structure. Let
$\mathcal {L}$
-pre-structure. Let
![]() $(\Delta , V)$
be a good value pair for
$(\Delta , V)$
be a good value pair for
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
-
(i) We say that
 $\mathcal {M}$
is
$\mathcal {M}$
is
 $(\Delta , V)$
-valued if for all
$(\Delta , V)$
-valued if for all
 $x, y\in M$
,
$x, y\in M$
,
 $d^M(x,y)\in \Delta $
and for all n-ary
$d^M(x,y)\in \Delta $
and for all n-ary
 $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
 $\overline {x}\in M^n$
,
$\overline {x}\in M^n$
,
 $R^M(\overline {x})\in V$
.
$R^M(\overline {x})\in V$
. -
(ii) Let
 $\mathcal {K}_{(\Delta , V)}$
be the class of all finite
$\mathcal {K}_{(\Delta , V)}$
be the class of all finite
 $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
 $\mathcal {L}$
-structures.
$\mathcal {L}$
-structures.
Lemma 5.3. Let
![]() $\mathcal {L}$
be a semiproper continuous signature.
$\mathcal {L}$
be a semiproper continuous signature.
-
(i) For any finite continuous
 $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
 $\mathcal {M}$
, there exists a finite good value pair
$\mathcal {M}$
, there exists a finite good value pair
 $(\Delta , V)$
for
$(\Delta , V)$
for
 $\mathcal {L}$
such that
$\mathcal {L}$
such that
 $\mathcal {M}$
is
$\mathcal {M}$
is
 $(\Delta , V)$
-valued.
$(\Delta , V)$
-valued. -
(ii) For any finite (countable, respectively) distance value set
 $\Delta $
and finite (countable, respectively)
$\Delta $
and finite (countable, respectively)
 $W\subseteq [0,1]$
, there exists a finite (countable, respectively) V such that
$W\subseteq [0,1]$
, there exists a finite (countable, respectively) V such that
 $W\subseteq V$
and
$W\subseteq V$
and
 $(\Delta , V)$
is a good value pair for
$(\Delta , V)$
is a good value pair for
 $\mathcal {L}$
.
$\mathcal {L}$
.
Proof (i) Let
Let
![]() $\delta $
be sufficiently large such that
$\delta $
be sufficiently large such that
![]() $\delta \geq \sup (P)$
and for any n-ary
$\delta \geq \sup (P)$
and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $\delta \geq \sup (I_{R,i})$
. Let
$\delta \geq \sup (I_{R,i})$
. Let
![]() $\Delta $
be the smallest distance value set such that
$\Delta $
be the smallest distance value set such that
![]() $P\subseteq \Delta $
and
$P\subseteq \Delta $
and
![]() $\sup (\Delta )=\delta \in \Delta $
. Since P is finite, so is
$\sup (\Delta )=\delta \in \Delta $
. Since P is finite, so is
![]() $\Delta $
.
$\Delta $
.
Let
 $$ \begin{align*}Q&=\{\mathfrak{u}_{R,i}(\delta)\,:\, R\in\mathcal{L} \mbox{ is}\ n\text{-}\mbox{ary}, 1\leq i\le n, \delta\in \Delta\},\\W&=\{R^M(\overline{x})\,:\, R\in\mathcal{L} \mbox{ is}\ n\text{-}\mbox{ary}, \overline{x}\in M^n\},\end{align*} $$
$$ \begin{align*}Q&=\{\mathfrak{u}_{R,i}(\delta)\,:\, R\in\mathcal{L} \mbox{ is}\ n\text{-}\mbox{ary}, 1\leq i\le n, \delta\in \Delta\},\\W&=\{R^M(\overline{x})\,:\, R\in\mathcal{L} \mbox{ is}\ n\text{-}\mbox{ary}, \overline{x}\in M^n\},\end{align*} $$
and
 $$ \begin{align*}V=\{0\}\cup W\cup ([0,1]\cap \left\{w-\sum_{i=1}^{\ell}q_i\,:\, w\in W,\ q_1,\dots, q_\ell\in Q\right\}).\end{align*} $$
$$ \begin{align*}V=\{0\}\cup W\cup ([0,1]\cap \left\{w-\sum_{i=1}^{\ell}q_i\,:\, w\in W,\ q_1,\dots, q_\ell\in Q\right\}).\end{align*} $$
Since
![]() $\mathcal {L}$
is semiproper, Q,
$\mathcal {L}$
is semiproper, Q,
![]() $W,$
and V are all finite. It is clear that
$W,$
and V are all finite. It is clear that
![]() $(\Delta , V)$
is a good value pair for
$(\Delta , V)$
is a good value pair for
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $(\Delta , V)$
-valued.
$(\Delta , V)$
-valued.
(ii) is proved similarly.
Definition 5.4. Let
![]() $\mathcal {L}$
be a continuous signature and
$\mathcal {L}$
be a continuous signature and
![]() $\mathcal {K}$
be a set of continuous
$\mathcal {K}$
be a set of continuous
![]() $\mathcal {L}$
-pre-structures.
$\mathcal {L}$
-pre-structures.
-
(i)
 $\mathcal {K}$
has the hereditary property (HP) if for any continuous
$\mathcal {K}$
has the hereditary property (HP) if for any continuous
 $\mathcal {L}$
-pre-structures
$\mathcal {L}$
-pre-structures
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $\mathcal {N}$
, if
$\mathcal {N}$
, if
 $\mathcal {M}$
is a substructure of
$\mathcal {M}$
is a substructure of
 $\mathcal {N}$
and
$\mathcal {N}$
and
 $\mathcal {N}\in \mathcal {K}$
, then
$\mathcal {N}\in \mathcal {K}$
, then
 $\mathcal {M}\in \mathcal {K}$
.
$\mathcal {M}\in \mathcal {K}$
. -
(ii)
 $\mathcal {K}$
has the joint embedding property (JEP) if for any
$\mathcal {K}$
has the joint embedding property (JEP) if for any
 $\mathcal {M}, \mathcal {N}\in \mathcal {K}$
there exist
$\mathcal {M}, \mathcal {N}\in \mathcal {K}$
there exist
 $\mathcal {P}\in \mathcal {K}$
and isomorphic embeddings
$\mathcal {P}\in \mathcal {K}$
and isomorphic embeddings
 $\varphi :\mathcal {M}\to \mathcal {P}$
and
$\varphi :\mathcal {M}\to \mathcal {P}$
and
 $\psi :\mathcal {N}\to \mathcal {P}$
.
$\psi :\mathcal {N}\to \mathcal {P}$
. 
-
(iii)
 $\mathcal {K}$
is a Fraïssé class if
$\mathcal {K}$
is a Fraïssé class if
 $\mathcal {K}$
has the HP, JEP, and AP.
$\mathcal {K}$
has the HP, JEP, and AP.
Our main theorem of the section is the following.
Theorem 5.5. Let
![]() $\mathcal {L}$
be a semiproper continuous signature and let
$\mathcal {L}$
be a semiproper continuous signature and let
![]() $(\Delta , V)$
be a countable good value pair for
$(\Delta , V)$
be a countable good value pair for
![]() $\mathcal {L}$
. Then the class
$\mathcal {L}$
. Then the class
![]() $\mathcal {K}_{(\Delta , V)}$
is a countable Fraïssé class.
$\mathcal {K}_{(\Delta , V)}$
is a countable Fraïssé class.
Proof It is obvious that
![]() $\mathcal {K}_{(\Delta , V)}$
is countable. The HP for
$\mathcal {K}_{(\Delta , V)}$
is countable. The HP for
![]() $\mathcal {K}_{(\Delta , V)}$
is obvious. For the JEP, suppose
$\mathcal {K}_{(\Delta , V)}$
is obvious. For the JEP, suppose
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are finite
$\mathcal {N}$
are finite
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-structures. Let X be the disjoint union of M and N. Let
$\mathcal {L}$
-structures. Let X be the disjoint union of M and N. Let
![]() $\delta \in \Delta $
be such that
$\delta \in \Delta $
be such that
![]() $\delta \geq {\mathrm {diam}}(M), {\mathrm {diam}}(N)$
and for any n-ary
$\delta \geq {\mathrm {diam}}(M), {\mathrm {diam}}(N)$
and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $\delta \geq \sup (I_{R,i})$
. Note that such
$\delta \geq \sup (I_{R,i})$
. Note that such
![]() $\delta $
exists since
$\delta $
exists since
![]() $(\Delta , V)$
is a good value pair for
$(\Delta , V)$
is a good value pair for
![]() $\mathcal {L}$
. Then define a metric
$\mathcal {L}$
. Then define a metric
![]() $d^X$
on X by
$d^X$
on X by
 $$ \begin{align*}d^X(x, y)=\left\{\begin{array}{@{}ll} d^{M}(x, y), & \mbox{ if}\ x, y\in M, \\ d^N(x,y), & \mbox{ if}\ x, y\in N, \\ \delta, & \mbox{ otherwise.} \end{array}\right. \end{align*} $$
$$ \begin{align*}d^X(x, y)=\left\{\begin{array}{@{}ll} d^{M}(x, y), & \mbox{ if}\ x, y\in M, \\ d^N(x,y), & \mbox{ if}\ x, y\in N, \\ \delta, & \mbox{ otherwise.} \end{array}\right. \end{align*} $$
For every
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^X$
is naturally defined on
$R^X$
is naturally defined on
and takes values in V. It is clear that
![]() $\mathcal {X}=(X, d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
$\mathcal {X}=(X, d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure. Then by Lemma 3.7,
$\mathcal {L}$
-pre-structure. Then by Lemma 3.7,
![]() $\mathcal {X}$
has a conservative extension
$\mathcal {X}$
has a conservative extension
![]() $\mathcal {P}$
. It is easy to see that
$\mathcal {P}$
. It is easy to see that
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
embed into
$\mathcal {N}$
embed into
![]() $\mathcal {P}$
as substructures.
$\mathcal {P}$
as substructures.
The proof of Theorem 3.8 gives the AP. Only note that for the partially defined structure
![]() $\mathcal {X}$
defined in that proof,
$\mathcal {X}$
defined in that proof,
![]() $d^X$
can be made to take values in
$d^X$
can be made to take values in
![]() $\Delta $
and for any
$\Delta $
and for any
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^X$
takes values in V. Then in the application of the proof of Lemma 3.7, for the amalgam
$R^X$
takes values in V. Then in the application of the proof of Lemma 3.7, for the amalgam
![]() $\mathcal {P}$
and any
$\mathcal {P}$
and any
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^P$
takes values in V. Thus the resulting amalgam
$R^P$
takes values in V. Thus the resulting amalgam
![]() $\mathcal {P}$
is an element of
$\mathcal {P}$
is an element of
![]() $\mathcal {K}_{(\Delta , V)}$
.
$\mathcal {K}_{(\Delta , V)}$
.
By a standard argument there exists a Fraïssé limit of the class
![]() $\mathcal {K}_{(\Delta , V)}$
when
$\mathcal {K}_{(\Delta , V)}$
when
![]() $\mathcal {L}$
is semiproper and
$\mathcal {L}$
is semiproper and
![]() $(\Delta , V)$
a countable good value pair for
$(\Delta , V)$
a countable good value pair for
![]() $\mathcal {L}$
. We denote it as
$\mathcal {L}$
. We denote it as
![]() $\mathbb {U}_{(\Delta , V)}$
.
$\mathbb {U}_{(\Delta , V)}$
.
![]() $\mathbb {U}_{(\Delta , V)}$
is the unique countable continuous
$\mathbb {U}_{(\Delta , V)}$
is the unique countable continuous
![]() $\mathcal {L}$
-pre-structure that is universal for all finite
$\mathcal {L}$
-pre-structure that is universal for all finite
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-structures and is ultrahomogeneous. It is also universal for all countable
$\mathcal {L}$
-structures and is ultrahomogeneous. It is also universal for all countable
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-pre-structures.
$\mathcal {L}$
-pre-structures.
It is well known that for any countable distance value set
![]() $\Delta $
, the class of all finite metric spaces whose distance takes values in
$\Delta $
, the class of all finite metric spaces whose distance takes values in
![]() $\Delta $
(known as
$\Delta $
(known as
![]() $\Delta $
-metric spaces) form a Fraïssé class (see, e.g., [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]), and the Fraïssé limit is denoted
$\Delta $
-metric spaces) form a Fraïssé class (see, e.g., [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]), and the Fraïssé limit is denoted
![]() $\mathbb {U}_{\Delta }$
. As usual,
$\mathbb {U}_{\Delta }$
. As usual,
![]() $\mathbb {U}_{\Delta }$
is characterized by the property that it is universal for all finite
$\mathbb {U}_{\Delta }$
is characterized by the property that it is universal for all finite
![]() $\Delta $
-metric spaces and it is ultrahomogeneous.
$\Delta $
-metric spaces and it is ultrahomogeneous.
By an argument identical to the proof of Theorem 4.12 (i)
![]() $\Rightarrow $
(ii), we have that if
$\Rightarrow $
(ii), we have that if
![]() $\mathcal {L}$
is a Lipschitz continuous signature and
$\mathcal {L}$
is a Lipschitz continuous signature and
![]() $(\Delta , V)$
is a countable good value pair for
$(\Delta , V)$
is a countable good value pair for
![]() $\mathcal {L}$
, then the metric space underlying
$\mathcal {L}$
, then the metric space underlying
![]() $\mathbb {U}_{(\Delta , V)}$
is isometric to
$\mathbb {U}_{(\Delta , V)}$
is isometric to
![]() $\mathbb {U}_{\Delta }$
.
$\mathbb {U}_{\Delta }$
.
When
![]() $\mathcal {L}$
is semiproper and
$\mathcal {L}$
is semiproper and
![]() $(\Delta , V)$
is a countable good value pair for
$(\Delta , V)$
is a countable good value pair for
![]() $\mathcal {L}$
, we consider the automorphism group of
$\mathcal {L}$
, we consider the automorphism group of
![]() $\mathbb {U}_{(\Delta , V)}$
and denote it as
$\mathbb {U}_{(\Delta , V)}$
and denote it as
![]() ${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
. Since
${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
. Since
![]() $\mathbb {U}_{(\Delta , V)}$
is countable, we may regard
$\mathbb {U}_{(\Delta , V)}$
is countable, we may regard
![]() ${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
as a subgroup of the infinite permutation group
${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
as a subgroup of the infinite permutation group
![]() $S_\infty $
. Under the usual topology of
$S_\infty $
. Under the usual topology of
![]() $S_\infty $
, it is a closed subgroup, hence is itself a Polish group. From the above discussions, we know that
$S_\infty $
, it is a closed subgroup, hence is itself a Polish group. From the above discussions, we know that
![]() ${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
is universal among all
${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
is universal among all
![]() ${\mathrm {Aut}}(\mathcal {M})$
for
${\mathrm {Aut}}(\mathcal {M})$
for
![]() $(\Delta ,V)$
-valued continuous
$(\Delta ,V)$
-valued continuous
![]() $\mathcal {L}$
-pre-structures
$\mathcal {L}$
-pre-structures
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
When
![]() $\Delta =\mathbb {Q}^+$
, we know by Lemma 5.3(ii) that there is a countable V such that
$\Delta =\mathbb {Q}^+$
, we know by Lemma 5.3(ii) that there is a countable V such that
![]() $\mathbb {Q}\cap [0,1]\subseteq V$
and
$\mathbb {Q}\cap [0,1]\subseteq V$
and
![]() $(\Delta , V)$
is a good value pair for
$(\Delta , V)$
is a good value pair for
![]() $\mathcal {L}$
. Moreover, there is a smallest such V, which we fix. We denote
$\mathcal {L}$
. Moreover, there is a smallest such V, which we fix. We denote
![]() $\mathbb {U}_{(\Delta , V)}$
also by
$\mathbb {U}_{(\Delta , V)}$
also by
![]() $\mathbb {QU}_{\mathcal {L}}$
following the convention for the analogous classical structure. We also call
$\mathbb {QU}_{\mathcal {L}}$
following the convention for the analogous classical structure. We also call
![]() $\mathbb {QU}_{\mathcal {L}}$
the rational Urysohn continuous
$\mathbb {QU}_{\mathcal {L}}$
the rational Urysohn continuous
![]() $\mathcal {L}$
-pre-structure.
$\mathcal {L}$
-pre-structure.
In the following we show that if
![]() $\mathcal {L}$
is proper, then the completion of
$\mathcal {L}$
is proper, then the completion of
![]() $\mathbb {QU}_{\mathcal {L}}$
is isomorphic to the unique separable Urysohn continuous
$\mathbb {QU}_{\mathcal {L}}$
is isomorphic to the unique separable Urysohn continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathbb {U}_{\mathcal {L}}$
.
$\mathbb {U}_{\mathcal {L}}$
.
Theorem 5.6. Let
![]() $\mathcal {L}$
be a proper continuous signature. Then the completion of
$\mathcal {L}$
be a proper continuous signature. Then the completion of
![]() $\mathbb {QU}_{\mathcal {L}}$
is isomorphic to
$\mathbb {QU}_{\mathcal {L}}$
is isomorphic to
![]() $\mathbb {U}_{\mathcal {L}}$
.
$\mathbb {U}_{\mathcal {L}}$
.
Proof Let
![]() $\Delta =\mathbb {Q}^+$
and let V be the smallest such that
$\Delta =\mathbb {Q}^+$
and let V be the smallest such that
![]() $\mathbb {Q}\cap [0,1]\subseteq V$
and
$\mathbb {Q}\cap [0,1]\subseteq V$
and
![]() $(\Delta , V)$
is a good value pair for
$(\Delta , V)$
is a good value pair for
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
![]() $\mathbb {QU}_{\mathcal {L}}$
obviously has the following rational Urysohn property: given any finite
$\mathbb {QU}_{\mathcal {L}}$
obviously has the following rational Urysohn property: given any finite
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
, a one-point extension
$\mathcal {M}$
, a one-point extension
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {M}$
that is
$\mathcal {M}$
that is
![]() $(\Delta , V)$
-valued, and an isomorphic embedding
$(\Delta , V)$
-valued, and an isomorphic embedding
![]() $\varphi $
from
$\varphi $
from
![]() $\mathcal {M}$
into
$\mathcal {M}$
into
![]() $\mathbb {QU}_{\mathcal {L}}$
, there is an isomorphic embedding
$\mathbb {QU}_{\mathcal {L}}$
, there is an isomorphic embedding
![]() $\psi $
from
$\psi $
from
![]() $\mathcal {N}$
into
$\mathcal {N}$
into
![]() $\mathbb {QU}_{\mathcal {L}}$
such that
$\mathbb {QU}_{\mathcal {L}}$
such that
![]() $\psi \,{\!\upharpoonright \!}\,\, M=\varphi $
.
$\psi \,{\!\upharpoonright \!}\,\, M=\varphi $
.
Using the rational Urysohn property to replace the Urysohn property, the proofs of Theorem 4.5 and Lemma 4.6 can be repeated so that the following statement holds: given any finite substructure
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\bar {\mathbb {QU}}_{\mathcal {L}}=\bar {\mathcal {M}}$
, a one-point extension
$\bar {\mathbb {QU}}_{\mathcal {L}}=\bar {\mathcal {M}}$
, a one-point extension
![]() $\mathcal {A}_x$
of
$\mathcal {A}_x$
of
![]() $\mathcal {A}$
, and
$\mathcal {A}$
, and
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $u\in \mathbb {QU}_{\mathcal {L}}$
such that
$u\in \mathbb {QU}_{\mathcal {L}}$
such that
and for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {y}\in A_x^n$
,
$\overline {y}\in A_x^n$
,
Then by repeating the proof of Theorem 4.8, again replacing the Urysohn property by the rational Urysohn property in the assumption, we get the Urysohn property for the completion of
![]() $\mathbb {QU}_{\mathcal {L}}$
. This shows that the completion of
$\mathbb {QU}_{\mathcal {L}}$
. This shows that the completion of
![]() $\mathbb {QU}_{\mathcal {L}}$
is isomorphic to
$\mathbb {QU}_{\mathcal {L}}$
is isomorphic to
![]() $\mathbb {U}_{\mathcal {L}}$
.
$\mathbb {U}_{\mathcal {L}}$
.
If
![]() $\mathcal {L}$
is proper, by Theorem 5.6 every element of
$\mathcal {L}$
is proper, by Theorem 5.6 every element of
![]() ${\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}})$
extends uniquely to an element of
${\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}})$
extends uniquely to an element of
![]() ${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
. Let
${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
. Let
![]() $\eta : {\mathrm { Aut}}(\mathbb {QU}_{\mathcal {L}}) \to {\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
be this canonical extension map. Then it is easy to see that
$\eta : {\mathrm { Aut}}(\mathbb {QU}_{\mathcal {L}}) \to {\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
be this canonical extension map. Then it is easy to see that
![]() $\eta $
is a group isomorphic embedding.
$\eta $
is a group isomorphic embedding.
Before closing this section we show that
![]() $\eta ({\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}}))$
is dense in
$\eta ({\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}}))$
is dense in
![]() ${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
. For this we need to fix some notation. For any continuous
${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
. For this we need to fix some notation. For any continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
with one-point extensions
$\mathcal {M}$
with one-point extensions
![]() $\mathcal {M}_x$
and
$\mathcal {M}_x$
and
![]() $\mathcal {M}_y$
, let
$\mathcal {M}_y$
, let
be defined as in Section 4.1. Let
![]() $A>\max \{NJ,1\}$
, where N and J are defined as in the proof of Theorem 4.5.
$A>\max \{NJ,1\}$
, where N and J are defined as in the proof of Theorem 4.5.
Lemma 5.7. Let
![]() $\mathcal {M}=\mathbb {QU}_{\mathcal {L}}$
,
$\mathcal {M}=\mathbb {QU}_{\mathcal {L}}$
,
![]() $\mathcal {A}$
be a finite substructure of
$\mathcal {A}$
be a finite substructure of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {A}_x$
and
$\mathcal {A}_x$
and
![]() $\mathcal {A}_y$
be one-point extensions of
$\mathcal {A}_y$
be one-point extensions of
![]() $\mathcal {A}$
, and
$\mathcal {A}$
, and
![]() $\epsilon>0$
. Suppose
$\epsilon>0$
. Suppose
![]() $y\in M$
,
$y\in M$
,
![]() $d^E_{\mathcal {A}}(x,y)<\epsilon $
, and there is
$d^E_{\mathcal {A}}(x,y)<\epsilon $
, and there is
![]() $x_0\in M$
such that
$x_0\in M$
such that
![]() $d^E_{\mathcal {A}}(x, x_0)=0$
. Then there is some
$d^E_{\mathcal {A}}(x, x_0)=0$
. Then there is some
![]() $x'\in M$
such that
$x'\in M$
such that
![]() $d^E_{\mathcal {A}}(x, x')=0$
and
$d^E_{\mathcal {A}}(x, x')=0$
and
![]() $d^{M}(x',y)<\epsilon $
.
$d^{M}(x',y)<\epsilon $
.
Proof Let
![]() $\Delta =\mathbb {Q}^+$
and let V be the smallest such that
$\Delta =\mathbb {Q}^+$
and let V be the smallest such that
![]() $\mathbb {Q}\cap [0,1]\subseteq V$
and
$\mathbb {Q}\cap [0,1]\subseteq V$
and
![]() $(\Delta , V)$
is a good value pair for
$(\Delta , V)$
is a good value pair for
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
By Lemma 4.7 there is an amalgam
![]() $\mathcal {A}_{xy}$
of both
$\mathcal {A}_{xy}$
of both
![]() $\mathcal {A}_x$
and
$\mathcal {A}_x$
and
![]() $\mathcal {A}_y$
such that
$\mathcal {A}_y$
such that
![]() $A_{xy}=A\cup \{x, y\}$
and
$A_{xy}=A\cup \{x, y\}$
and
![]() $d^{A_{xy}}(x,y)=d^E_{\mathcal {A}}(x,y)$
. We define a finite continuous
$d^{A_{xy}}(x,y)=d^E_{\mathcal {A}}(x,y)$
. We define a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {F}$
where
$\mathcal {F}$
where
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {A}_{xy}$
agree on everything except that
$\mathcal {A}_{xy}$
agree on everything except that
![]() $d^F(x,y)$
is a rational number such that both
$d^F(x,y)$
is a rational number such that both
and
It follows from our assumptions that
![]() $\mathcal {F}$
is a finite
$\mathcal {F}$
is a finite
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-structure that is an extension of
$\mathcal {L}$
-structure that is an extension of
![]() $\mathcal {A}_y$
. By the rational Urysohn property of
$\mathcal {A}_y$
. By the rational Urysohn property of
![]() $\mathcal {M}$
, we obtain a point
$\mathcal {M}$
, we obtain a point
![]() $x'\in M$
such that
$x'\in M$
such that
![]() $d^E_{\mathcal {A}}(x, x')=0$
and
$d^E_{\mathcal {A}}(x, x')=0$
and
![]() $d^M(x',y)=d^F(x, y)<\epsilon $
.
$d^M(x',y)=d^F(x, y)<\epsilon $
.
Theorem 5.8.
![]() $\eta ({\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}}))$
is dense in
$\eta ({\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}}))$
is dense in
![]() ${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
.
${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
.
Proof Let
![]() $\mathcal {M}=\mathbb {QU}_{\mathcal {L}}$
and
$\mathcal {M}=\mathbb {QU}_{\mathcal {L}}$
and
![]() $\bar {\mathcal {M}}=\mathbb {U}_{\mathcal {L}}$
. Let
$\bar {\mathcal {M}}=\mathbb {U}_{\mathcal {L}}$
. Let
![]() $g\in {\mathrm {Aut}}(\bar {\mathcal {M}})$
,
$g\in {\mathrm {Aut}}(\bar {\mathcal {M}})$
,
![]() $x_1,\dots , x_n\in \bar {\mathcal {M}}$
and
$x_1,\dots , x_n\in \bar {\mathcal {M}}$
and
![]() ${\epsilon>0}$
. We will define
${\epsilon>0}$
. We will define
![]() $y_1,\dots , y_n, z_1,\dots , z_n\in M$
such that the map
$y_1,\dots , y_n, z_1,\dots , z_n\in M$
such that the map
![]() $y_i\mapsto z_i$
,
$y_i\mapsto z_i$
,
![]() $1\leq i\leq n$
, is a partial isomorphism of
$1\leq i\leq n$
, is a partial isomorphism of
![]() $\mathcal {M}$
, and for all
$\mathcal {M}$
, and for all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
and
First, let
![]() $y_1,\dots , y_n\in M$
be such that
$y_1,\dots , y_n\in M$
be such that
![]() $d^{\bar {M}}(x_i,y_i)<\epsilon $
for all
$d^{\bar {M}}(x_i,y_i)<\epsilon $
for all
![]() $1\leq i\leq n$
. Let
$1\leq i\leq n$
. Let
![]() $u_1, \dots , u_n\in M$
be such that
$u_1, \dots , u_n\in M$
be such that
![]() $d^E_{\varnothing }(g(y_i), u_i)<\epsilon $
and
$d^E_{\varnothing }(g(y_i), u_i)<\epsilon $
and
![]() $d^{\bar {M}}(g(y_i), u_i)<\epsilon $
. We define
$d^{\bar {M}}(g(y_i), u_i)<\epsilon $
. We define
![]() $z_1,\dots , z_n\in M$
by induction on
$z_1,\dots , z_n\in M$
by induction on
![]() $1\leq i\leq n$
with the following inductive hypothesis: letting
$1\leq i\leq n$
with the following inductive hypothesis: letting
![]() $A_{i-1}=\{z_1,\dots , z_{i-1}\}$
, the map
$A_{i-1}=\{z_1,\dots , z_{i-1}\}$
, the map
![]() $y_j\mapsto z_j$
,
$y_j\mapsto z_j$
,
![]() $1\leq j\leq i-1$
, is a partial isomorphism of
$1\leq j\leq i-1$
, is a partial isomorphism of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $d^{\bar {M}}(u_j, z_j)<2jA^j\epsilon $
for all
$d^{\bar {M}}(u_j, z_j)<2jA^j\epsilon $
for all
![]() $1\leq j\leq i-1$
. Let
$1\leq j\leq i-1$
. Let
![]() $F_{i-1}=\{y_1,\dots , y_{i-1}\}$
. Then by our inductive hypothesis
$F_{i-1}=\{y_1,\dots , y_{i-1}\}$
. Then by our inductive hypothesis
![]() $\mathcal {A}_{i-1}$
and
$\mathcal {A}_{i-1}$
and
![]() $\mathcal {F}_{i-1}$
are isomorphic. Let
$\mathcal {F}_{i-1}$
are isomorphic. Let
![]() $\pi _{i-1}: F_{i-1}\to A_{i-1}$
be the isomorphism given by
$\pi _{i-1}: F_{i-1}\to A_{i-1}$
be the isomorphism given by
![]() $\pi _{i-1}(y_j)=z_j$
for
$\pi _{i-1}(y_j)=z_j$
for
![]() $1\leq j\leq i-1$
. Consider the one-point extension of
$1\leq j\leq i-1$
. Consider the one-point extension of
![]() $\mathcal {F}_{i-1}$
by
$\mathcal {F}_{i-1}$
by
![]() $y_i$
. Via
$y_i$
. Via
![]() $\pi _{i-1}$
this gives a one-point extension of
$\pi _{i-1}$
this gives a one-point extension of
![]() $\mathcal {A}_{i-1}$
by a point which we denote by
$\mathcal {A}_{i-1}$
by a point which we denote by
![]() $v_i$
. Consider also the one-point extension of
$v_i$
. Consider also the one-point extension of
![]() $\mathcal {A}_{i-1}$
by
$\mathcal {A}_{i-1}$
by
![]() $u_i$
. In the following calculation we denote
$u_i$
. In the following calculation we denote
![]() $\mathcal {A}_{i-1}$
by
$\mathcal {A}_{i-1}$
by
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {F}_{i-1}$
by
$\mathcal {F}_{i-1}$
by
![]() $\mathcal {F}$
for notational simplicity.
$\mathcal {F}$
for notational simplicity.
For any unary
![]() $R\in \mathcal {L}$
, we have
$R\in \mathcal {L}$
, we have
 $$ \begin{align*}\mathfrak{u}^*_{R,1}(|R^{A_{u_i}}(u_i)-R^{A_{v_i}}(v_i)|) &= \mathfrak{u}^*_{R,1}(|R^{A_{u_i}}(u_i)-R^{F_{y_i}}(y_i)|) \\&= \mathfrak{u}^*_{R,1}(|R^{A_{u_i}}(u_i)-R^{g(F)_{g(y_i)}}(g(y_i))|) \\&\leq d^E_{\varnothing}(u_i,g(y_i))<\epsilon. \end{align*} $$
$$ \begin{align*}\mathfrak{u}^*_{R,1}(|R^{A_{u_i}}(u_i)-R^{A_{v_i}}(v_i)|) &= \mathfrak{u}^*_{R,1}(|R^{A_{u_i}}(u_i)-R^{F_{y_i}}(y_i)|) \\&= \mathfrak{u}^*_{R,1}(|R^{A_{u_i}}(u_i)-R^{g(F)_{g(y_i)}}(g(y_i))|) \\&\leq d^E_{\varnothing}(u_i,g(y_i))<\epsilon. \end{align*} $$
Thus
![]() $\mu (u_i,v_i)<\epsilon $
.
$\mu (u_i,v_i)<\epsilon $
.
Let
![]() $1\leq j\leq i-1$
be such that
$1\leq j\leq i-1$
be such that
![]() $\lambda (u_i, v_i)=|d^{A_{u_i}}(u_i, z_j)-d^{A_{v_i}}(v_i,z_j)|$
. Then
$\lambda (u_i, v_i)=|d^{A_{u_i}}(u_i, z_j)-d^{A_{v_i}}(v_i,z_j)|$
. Then
 $$ \begin{align*}\lambda(u_i, v_i)&=|d^{A_{u_i}}(u_i, z_j)-d^{A_{v_i}}(v_i,z_j)| \\&= |d^{A_{u_i}}(u_i, z_j)-d^{F_{y_i}}(y_i,y_j)| \\&= |d^{\bar{M}}(u_i, z_j)-d^{\bar{M}}(y_i,y_j)| \\&= |d^{\bar{M}}(u_i,z_j)-d^{\bar{M}}(g(y_i), g(y_j))| \\&\leq d^{\bar{M}}(u_i, g(y_i))+d^{\bar{M}}(g(y_j),z_j) \\&\leq d^{\bar{M}}(u_i, g(y_i))+d^{\bar{M}}(g(y_j),u_j)+d^{\bar{M}}(u_j, z_j) \\&\leq \epsilon+\epsilon+2jA^j\epsilon \leq 2iA^i\epsilon. \end{align*} $$
$$ \begin{align*}\lambda(u_i, v_i)&=|d^{A_{u_i}}(u_i, z_j)-d^{A_{v_i}}(v_i,z_j)| \\&= |d^{A_{u_i}}(u_i, z_j)-d^{F_{y_i}}(y_i,y_j)| \\&= |d^{\bar{M}}(u_i, z_j)-d^{\bar{M}}(y_i,y_j)| \\&= |d^{\bar{M}}(u_i,z_j)-d^{\bar{M}}(g(y_i), g(y_j))| \\&\leq d^{\bar{M}}(u_i, g(y_i))+d^{\bar{M}}(g(y_j),z_j) \\&\leq d^{\bar{M}}(u_i, g(y_i))+d^{\bar{M}}(g(y_j),u_j)+d^{\bar{M}}(u_j, z_j) \\&\leq \epsilon+\epsilon+2jA^j\epsilon \leq 2iA^i\epsilon. \end{align*} $$
Finally, let
![]() $R\in \mathcal {L}$
be n-ary where
$R\in \mathcal {L}$
be n-ary where
![]() $n\geq 2$
, and let
$n\geq 2$
, and let
![]() $\overline {w}\in A_{u_i}^n\setminus A^n$
. Define
$\overline {w}\in A_{u_i}^n\setminus A^n$
. Define
![]() $\overline {w}'\in g(F)_{g(y_i)}^n$
by
$\overline {w}'\in g(F)_{g(y_i)}^n$
by
 $$ \begin{align*}w'_k=\left\{\begin{array}{@{}ll} g(y_j), & \mbox{ if}\ w_k=z_j\ \mbox{ for some}\ 1\leq j\leq i-1, \\ g(y_i), & \mbox{ if}\ w_k=u_i. \end{array}\right. \end{align*} $$
$$ \begin{align*}w'_k=\left\{\begin{array}{@{}ll} g(y_j), & \mbox{ if}\ w_k=z_j\ \mbox{ for some}\ 1\leq j\leq i-1, \\ g(y_i), & \mbox{ if}\ w_k=u_i. \end{array}\right. \end{align*} $$
We have
 $$ \begin{align*}& \|\overline{w}\|^{-1}\left|R^{A_{u_i}}(\overline{w})-R^{A_{v_i}}(\overline{w}(v_i|u_i))\right| \\&\quad = \|\overline{w}\|^{-1}\left|R^{A_{u_i}}(\overline{w})-R^{g(F)_{g(y_i)}}(\overline{w}')\right| \\&\quad \leq A(d^{\bar{M}}(u_i,g(y_i))+\max\{d^{\bar{M}}(z_j, g(y_j))\,:\, 1\leq j\leq i-1\}) \\&\quad \leq A(d^{\bar{M}}(u_i,g(y_i))+\max\{d^{\bar{M}}(z_j, u_j)+ d^{\bar{M}}(u_j, g(y_j))\,:\, 1\leq j\leq i-1\}) \\&\quad \leq A(\epsilon+2(i-1)A^{i-1}\epsilon+\epsilon)\leq 2iA^i\epsilon. \end{align*} $$
$$ \begin{align*}& \|\overline{w}\|^{-1}\left|R^{A_{u_i}}(\overline{w})-R^{A_{v_i}}(\overline{w}(v_i|u_i))\right| \\&\quad = \|\overline{w}\|^{-1}\left|R^{A_{u_i}}(\overline{w})-R^{g(F)_{g(y_i)}}(\overline{w}')\right| \\&\quad \leq A(d^{\bar{M}}(u_i,g(y_i))+\max\{d^{\bar{M}}(z_j, g(y_j))\,:\, 1\leq j\leq i-1\}) \\&\quad \leq A(d^{\bar{M}}(u_i,g(y_i))+\max\{d^{\bar{M}}(z_j, u_j)+ d^{\bar{M}}(u_j, g(y_j))\,:\, 1\leq j\leq i-1\}) \\&\quad \leq A(\epsilon+2(i-1)A^{i-1}\epsilon+\epsilon)\leq 2iA^i\epsilon. \end{align*} $$
This implies that
![]() $\rho (u_i,v_i)<2iA^i\epsilon $
.
$\rho (u_i,v_i)<2iA^i\epsilon $
.
Combining the above computations, we get
![]() $d^E_{\mathcal {A}}(u_i,v_i)<2iAi\epsilon $
. By Lemma 5.7, there is some
$d^E_{\mathcal {A}}(u_i,v_i)<2iAi\epsilon $
. By Lemma 5.7, there is some
![]() $z_i\in M$
such that the map
$z_i\in M$
such that the map
![]() $y_j\mapsto z_j$
,
$y_j\mapsto z_j$
,
![]() $1\leq j\leq i$
, is a partial isomorphism of
$1\leq j\leq i$
, is a partial isomorphism of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $d^M(u_j, z_j)<2iA^i\epsilon $
. This completes the induction.
$d^M(u_j, z_j)<2iA^i\epsilon $
. This completes the induction.
We note that for any
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
as desired.
6. Coherent EPPA for continuous structures
In this section we continue to work with a semiproper continuous signature
![]() $\mathcal {L}$
. We prove that the class of all finite continuous
$\mathcal {L}$
. We prove that the class of all finite continuous
![]() $\mathcal {L}$
-structures has the coherent EPPA as defined by Hrushovski [Reference Hrushovski11] and Siniora–Solecki [Reference Siniora and Solecki16].
$\mathcal {L}$
-structures has the coherent EPPA as defined by Hrushovski [Reference Hrushovski11] and Siniora–Solecki [Reference Siniora and Solecki16].
Theorem 6.1. Let
![]() $\mathcal {L}$
be a semiproper continuous signature and let
$\mathcal {L}$
be a semiproper continuous signature and let
![]() $\mathcal {M}$
be a finite continuous
$\mathcal {M}$
be a finite continuous
![]() $\mathcal {L}$
-structure. There is a finite continuous
$\mathcal {L}$
-structure. There is a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
such that:
$\mathcal {N}$
such that:
-
(i)
 $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
 $\mathcal {M}$
;
$\mathcal {M}$
; -
(ii) there is a map
 $\phi $
from the set
$\phi $
from the set
 ${\mathrm {Part}}(\mathcal {M})$
of all partial automorphism of
${\mathrm {Part}}(\mathcal {M})$
of all partial automorphism of
 $\mathcal {M}$
to the set
$\mathcal {M}$
to the set
 ${\mathrm {Aut}}(\mathcal {N})$
of all automorphism of
${\mathrm {Aut}}(\mathcal {N})$
of all automorphism of
 $\mathcal {N}$
such that for any
$\mathcal {N}$
such that for any
 $\pi \in {\mathrm {Part}}(\mathcal {M})$
,
$\pi \in {\mathrm {Part}}(\mathcal {M})$
,
 $\phi (\pi )$
extends
$\phi (\pi )$
extends
 $\pi $
;
$\pi $
; -
(iii) for the map
 $\phi $
in (ii) we have that for all
$\phi $
in (ii) we have that for all
 $\pi , \tau \in {\mathrm {Part}}(\mathcal {M})$
, if
$\pi , \tau \in {\mathrm {Part}}(\mathcal {M})$
, if
 ${\mathrm {range}}(\tau )={\mathrm {dom}}(\pi )$
then
${\mathrm {range}}(\tau )={\mathrm {dom}}(\pi )$
then  $$ \begin{align*}\phi(\pi\circ \tau)=\phi(\pi)\circ \phi(\tau).\end{align*} $$
$$ \begin{align*}\phi(\pi\circ \tau)=\phi(\pi)\circ \phi(\tau).\end{align*} $$
Proof Let
and
We introduce a new binary relation symbol
![]() $D_p$
for each
$D_p$
for each
![]() $p\in P$
and an n-ary relation symbol
$p\in P$
and an n-ary relation symbol
![]() $R_{v}$
for each n-ary
$R_{v}$
for each n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $v\in V$
. Let
$v\in V$
. Let
![]() $\mathcal {L}^*$
be the classical signature consisting of all
$\mathcal {L}^*$
be the classical signature consisting of all
![]() $D_p$
and
$D_p$
and
![]() $R_v$
for
$R_v$
for
![]() $p\in P$
,
$p\in P$
,
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $v\in V$
. Let
$v\in V$
. Let
![]() $\mathcal {T}$
be the collection of all finite classical
$\mathcal {T}$
be the collection of all finite classical
![]() $\mathcal {L}^*$
-structures
$\mathcal {L}^*$
-structures
![]() $\mathcal {S}$
satisfying one of the following conditions:
$\mathcal {S}$
satisfying one of the following conditions:
-
(a) for some
 $m\geq 1$
and
$m\geq 1$
and
 $p, p_1, \dots , p_m\in P$
such that
$p, p_1, \dots , p_m\in P$
such that  $$ \begin{align*}\displaystyle\sum_{i=1}^m p_i<p,\end{align*} $$
$$ \begin{align*}\displaystyle\sum_{i=1}^m p_i<p,\end{align*} $$
 $\mathcal {S}$
has at most
$\mathcal {S}$
has at most
 $m+1$
elements and there are
$m+1$
elements and there are
 $z_0, z_1, \dots , z_m\in S$
such that or
$z_0, z_1, \dots , z_m\in S$
such that or $$ \begin{align*}\mathcal{S}\models D_{p}(z_0, z_m)\wedge D_{p}(z_m, z_0)\wedge \bigwedge_{1\leq i\leq m} (D_{p_i}(z_{i-1}, z_i)\wedge D_{p_i}(z_i,z_{i-1}));\end{align*} $$
$$ \begin{align*}\mathcal{S}\models D_{p}(z_0, z_m)\wedge D_{p}(z_m, z_0)\wedge \bigwedge_{1\leq i\leq m} (D_{p_i}(z_{i-1}, z_i)\wedge D_{p_i}(z_i,z_{i-1}));\end{align*} $$
-
(b) for some n-ary
 $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
 $v, v'\in V$
,
$v, v'\in V$
,
 $m_1,\dots , m_n\geq 1$
and such that
$m_1,\dots , m_n\geq 1$
and such that $$ \begin{align*}p_{1,1}, \dots, p_{1, m_1}, p_{2, 1},\dots, p_{2, m_2},\dots, p_{n, 1}, \dots, p_{n, m_n}\in P\end{align*} $$
$$ \begin{align*}p_{1,1}, \dots, p_{1, m_1}, p_{2, 1},\dots, p_{2, m_2},\dots, p_{n, 1}, \dots, p_{n, m_n}\in P\end{align*} $$
 $$ \begin{align*}\displaystyle\sum_{i=1}^n\sum_{j=1}^{m_i}\mathfrak{u}_{R,i}(p_{i,j})<|v-v'|,\end{align*} $$
$$ \begin{align*}\displaystyle\sum_{i=1}^n\sum_{j=1}^{m_i}\mathfrak{u}_{R,i}(p_{i,j})<|v-v'|,\end{align*} $$
 $\mathcal {S}$
has at most
$\mathcal {S}$
has at most
 $\sum _{i=1}^n(m_i+1)=n+\sum _{i=1}^nm_i$
elements and there are such that
$\sum _{i=1}^n(m_i+1)=n+\sum _{i=1}^nm_i$
elements and there are such that $$ \begin{align*}z_{1, 0}, \dots, z_{1, m_1}, z_{2,0}, \dots, z_{2, m_2}, \dots, z_{n, 0}, \dots, z_{n, m_n}\in S\end{align*} $$
and
$$ \begin{align*}z_{1, 0}, \dots, z_{1, m_1}, z_{2,0}, \dots, z_{2, m_2}, \dots, z_{n, 0}, \dots, z_{n, m_n}\in S\end{align*} $$
and $$ \begin{align*}\mathcal{S}\models \bigwedge_{1\leq i\leq n}\bigwedge_{1\leq j\leq m_i} (D_{p_{i,j}}(z_{i,j-1}, z_{i,j})\wedge D_{p_{i,j}}(z_{i,j}, z_{i,j-1}))\end{align*} $$
or
$$ \begin{align*}\mathcal{S}\models \bigwedge_{1\leq i\leq n}\bigwedge_{1\leq j\leq m_i} (D_{p_{i,j}}(z_{i,j-1}, z_{i,j})\wedge D_{p_{i,j}}(z_{i,j}, z_{i,j-1}))\end{align*} $$
or $$ \begin{align*}\mathcal{S}\models R_{v}(z_{1,0}, z_{2,0},\dots, z_{n, 0}) \wedge R_{v'}(z_{1, m_1}, z_{2, m_2}, \dots, z_{n, m_n});\end{align*} $$
$$ \begin{align*}\mathcal{S}\models R_{v}(z_{1,0}, z_{2,0},\dots, z_{n, 0}) \wedge R_{v'}(z_{1, m_1}, z_{2, m_2}, \dots, z_{n, m_n});\end{align*} $$
-
(c) for some n-ary
 $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
 $v\neq v'\in V$
,
$v\neq v'\in V$
,
 $\mathcal {S}$
has at most n elements and there are
$\mathcal {S}$
has at most n elements and there are
 $x_1, \dots , x_n\in S$
such that
$x_1, \dots , x_n\in S$
such that  $$ \begin{align*}\mathcal{S}\models R_v(x_1,\dots, x_n)\wedge R_{v'}(x_1,\dots, x_n).\end{align*} $$
$$ \begin{align*}\mathcal{S}\models R_v(x_1,\dots, x_n)\wedge R_{v'}(x_1,\dots, x_n).\end{align*} $$
Since D and V are finite,
![]() $\mathcal {T}$
is also finite.
$\mathcal {T}$
is also finite.
For any continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {A}$
we obtain a classical
$\mathcal {A}$
we obtain a classical
![]() $\mathcal {L}^*$
-structure
$\mathcal {L}^*$
-structure
![]() $\mathcal {A}^*$
in the obvious way: for
$\mathcal {A}^*$
in the obvious way: for
![]() $x, y\in A^*$
and
$x, y\in A^*$
and
![]() $p\in P$
, define
$p\in P$
, define
and for any n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $v\in V$
and
$v\in V$
and
![]() $\overline {x}\in ({A}^*)^n$
, define
$\overline {x}\in ({A}^*)^n$
, define
By Lemma 5.3(i) there is a finite good value pair
![]() $(\Delta , W)$
for
$(\Delta , W)$
for
![]() $\mathcal {L}$
such that
$\mathcal {L}$
such that
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $(\Delta , W)$
-valued. Moreover,
$(\Delta , W)$
-valued. Moreover,
![]() $P\subseteq \Delta $
and
$P\subseteq \Delta $
and
![]() $V\subseteq W$
. By Theorem 5.5 the class
$V\subseteq W$
. By Theorem 5.5 the class
![]() $\mathcal {K}_{(\Delta , W)}$
is a countable Fraïssé class and thus has a Fraïssé limit
$\mathcal {K}_{(\Delta , W)}$
is a countable Fraïssé class and thus has a Fraïssé limit
![]() $\mathbb {U}_{(\Delta , W)}$
. Then
$\mathbb {U}_{(\Delta , W)}$
. Then
![]() $\mathbb {U}_{(\Delta , W)}^*$
is a classical
$\mathbb {U}_{(\Delta , W)}^*$
is a classical
![]() $\mathcal {L}^*$
-structure which extends
$\mathcal {L}^*$
-structure which extends
![]() $\mathcal {M}^*$
such that any partial automorphism of
$\mathcal {M}^*$
such that any partial automorphism of
![]() $\mathcal {M}^*$
extends to an automorphism of
$\mathcal {M}^*$
extends to an automorphism of
![]() $\mathbb {U}_{(\Delta , W)}^*$
. Moreover,
$\mathbb {U}_{(\Delta , W)}^*$
. Moreover,
![]() $\mathbb {U}_{(\Delta , W)}^*$
is
$\mathbb {U}_{(\Delta , W)}^*$
is
![]() $\mathcal {T}$
-free under homomorphisms, i.e., there is no
$\mathcal {T}$
-free under homomorphisms, i.e., there is no
![]() $\mathcal {S}\in \mathcal {T}$
and homomorphism from
$\mathcal {S}\in \mathcal {T}$
and homomorphism from
![]() $\mathcal {S}$
into
$\mathcal {S}$
into
![]() $\mathbb {U}_{(\Delta , W)}^*$
.
$\mathbb {U}_{(\Delta , W)}^*$
.
By Theorem 1.11 of [Reference Siniora and Solecki16] there is a finite
![]() $\mathcal {L}^*$
-structure
$\mathcal {L}^*$
-structure
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
![]() $\mathcal {X}$
is an extension of
$\mathcal {X}$
is an extension of
![]() $\mathcal {M}^*$
and there is a map
$\mathcal {M}^*$
and there is a map
![]() $\psi : {\mathrm { Part}}(\mathcal {M}^*)\to {\mathrm {Aut}}(\mathcal {X})$
such that for any
$\psi : {\mathrm { Part}}(\mathcal {M}^*)\to {\mathrm {Aut}}(\mathcal {X})$
such that for any
![]() $\pi \in {\mathrm {Part}}(\mathcal {M}^*)$
,
$\pi \in {\mathrm {Part}}(\mathcal {M}^*)$
,
![]() $\psi (\pi )$
extends
$\psi (\pi )$
extends
![]() $\pi $
, and for all
$\pi $
, and for all
![]() $\pi , \tau \in {\mathrm {Part}}(\mathcal {M}^*)$
, if
$\pi , \tau \in {\mathrm {Part}}(\mathcal {M}^*)$
, if
![]() ${\mathrm {dom}}(\pi )={\mathrm {range}}(\tau )$
, then
${\mathrm {dom}}(\pi )={\mathrm {range}}(\tau )$
, then
Define an equivalence relation
![]() $\sim $
on X by
$\sim $
on X by
![]() $x\sim y$
iff there are
$x\sim y$
iff there are
![]() $x=z_0, \dots , z_m=y\in X$
and
$x=z_0, \dots , z_m=y\in X$
and
![]() $p_1,\dots , p_m\in P$
such that
$p_1,\dots , p_m\in P$
such that
Clearly M is contained in one of the
![]() $\sim $
-equivalence classes. We denote this class by Y. Let
$\sim $
-equivalence classes. We denote this class by Y. Let
![]() $\mathcal {Y}$
be the substructure of
$\mathcal {Y}$
be the substructure of
![]() $\mathcal {X}$
with domain Y. We define a metric
$\mathcal {X}$
with domain Y. We define a metric
![]() $d^Y$
on Y as follows. For any
$d^Y$
on Y as follows. For any
![]() $x, y\in Y$
, define
$x, y\in Y$
, define
![]() $d^Y(x, y)=0$
if
$d^Y(x, y)=0$
if
![]() $x=y$
, and
$x=y$
, and
 $$ \begin{align*}d^Y(x, y)&=\inf\left\{ \displaystyle\sum_{i=1}^m p_i\right. \,:\, p_1,\dots, p_m\in P, \exists z_0=x, z_1,\dots, z_m=y\in Y \\& \qquad\qquad \mbox{such that } \left.\mathcal{X}\models \displaystyle\bigwedge_{1\leq i\leq m} (D_{p_i}(z_{i-1}, z_i)\wedge D_{p_i}(z_i,z_{i-1}))\right\}\end{align*} $$
$$ \begin{align*}d^Y(x, y)&=\inf\left\{ \displaystyle\sum_{i=1}^m p_i\right. \,:\, p_1,\dots, p_m\in P, \exists z_0=x, z_1,\dots, z_m=y\in Y \\& \qquad\qquad \mbox{such that } \left.\mathcal{X}\models \displaystyle\bigwedge_{1\leq i\leq m} (D_{p_i}(z_{i-1}, z_i)\wedge D_{p_i}(z_i,z_{i-1}))\right\}\end{align*} $$
if
![]() $x\neq y$
. Since
$x\neq y$
. Since
![]() $\mathcal {Y}$
is
$\mathcal {Y}$
is
![]() $\mathcal {T}$
-free, it follows that
$\mathcal {T}$
-free, it follows that
![]() $d^Y$
is a metric on Y and that
$d^Y$
is a metric on Y and that
![]() $(Y, d^Y)$
is an extension of
$(Y, d^Y)$
is an extension of
![]() $(M, d^M)$
as a metric space.
$(M, d^M)$
as a metric space.
For each nonempty
![]() $\pi \in {\mathrm {Part}}(\mathcal {M}^*)$
,
$\pi \in {\mathrm {Part}}(\mathcal {M}^*)$
,
![]() $\psi (\pi )\in {\mathrm {Aut}}(\mathcal {X})$
must fix Y setwise, thus
$\psi (\pi )\in {\mathrm {Aut}}(\mathcal {X})$
must fix Y setwise, thus
![]() $\psi (\pi )\,{\!\upharpoonright \!}\,\, Y$
is an automorphism of
$\psi (\pi )\,{\!\upharpoonright \!}\,\, Y$
is an automorphism of
![]() $\mathcal {Y}$
still extending
$\mathcal {Y}$
still extending
![]() $\pi $
, which implies that
$\pi $
, which implies that
![]() $\psi (\pi )\,{\!\upharpoonright \!}\,\, Y$
is an isometry of
$\psi (\pi )\,{\!\upharpoonright \!}\,\, Y$
is an isometry of
![]() $(Y, d^Y)$
extending
$(Y, d^Y)$
extending
![]() $\pi $
as a partial isometry of
$\pi $
as a partial isometry of
![]() $(M, d^M)$
.
$(M, d^M)$
.
We continue to define a partially defined continuous
![]() $\mathcal {L}$
-pre-structure on Y. For any n-ary
$\mathcal {L}$
-pre-structure on Y. For any n-ary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $v\in V$
, and
$v\in V$
, and
![]() $\overline {x}\in Y^n$
, let
$\overline {x}\in Y^n$
, let
![]() $R^Y(\overline {x})=v$
iff
$R^Y(\overline {x})=v$
iff
![]() $\mathcal {X}\models R_v(\overline {x})$
. Thus
$\mathcal {X}\models R_v(\overline {x})$
. Thus
Since
![]() $\mathcal {Y}$
is
$\mathcal {Y}$
is
![]() $\mathcal {T}$
-free, it follows that for any n-ary
$\mathcal {T}$
-free, it follows that for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {x}, \overline {y}\in {\mathrm {dom}}(R^Y)$
, we have
$\overline {x}, \overline {y}\in {\mathrm {dom}}(R^Y)$
, we have
![]() $R^Y(\overline {x}), R^Y(\overline {y})\in V$
, and
$R^Y(\overline {x}), R^Y(\overline {y})\in V$
, and
Hence
![]() $(Y, d^Y, (R^Y)_{R\in \mathcal {L}})$
is a partially defined continuous
$(Y, d^Y, (R^Y)_{R\in \mathcal {L}})$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure.
$\mathcal {L}$
-pre-structure.
Let
![]() $\mathcal {N}$
be a continuous
$\mathcal {N}$
be a continuous
![]() $\mathcal {L}$
-pre-structure that is a conservative extension of
$\mathcal {L}$
-pre-structure that is a conservative extension of
given by Lemma 3.7. Then
![]() $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
![]() $\mathcal {M}$
. For any
$\mathcal {M}$
. For any
![]() $\pi \in {\mathrm {Part}}(\mathcal {M})$
, let
$\pi \in {\mathrm {Part}}(\mathcal {M})$
, let
![]() $\phi (\pi )=\psi (\pi )\,{\!\upharpoonright \!}\,\, Y$
. To complete our proof, it suffices to show that for any
$\phi (\pi )=\psi (\pi )\,{\!\upharpoonright \!}\,\, Y$
. To complete our proof, it suffices to show that for any
![]() $\pi \in {\mathrm { Part}}(\mathcal {M})$
,
$\pi \in {\mathrm { Part}}(\mathcal {M})$
,
![]() $\phi (\pi )\in {\mathrm {Aut}}(\mathcal {N})$
. For this, we only note that for any n-ary
$\phi (\pi )\in {\mathrm {Aut}}(\mathcal {N})$
. For this, we only note that for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {z}\in N^n=Y^n$
,
$\overline {z}\in N^n=Y^n$
,
Thus
![]() $R^N(\overline {z})=R^N(\phi (\pi )(\overline {z}))$
since
$R^N(\overline {z})=R^N(\phi (\pi )(\overline {z}))$
since
![]() $\phi (\pi )(\overline {x})\in {\mathrm {dom}}(R^Y)$
iff
$\phi (\pi )(\overline {x})\in {\mathrm {dom}}(R^Y)$
iff
![]() $\overline {x}\in {\mathrm {dom}}(R^Y)$
, and for
$\overline {x}\in {\mathrm {dom}}(R^Y)$
, and for
![]() $\overline {x}\in {\mathrm {dom}}(R^Y)$
,
$\overline {x}\in {\mathrm {dom}}(R^Y)$
,
![]() $R^Y(\overline {x})=R^Y(\phi (\pi )(\overline {x}))$
.
$R^Y(\overline {x})=R^Y(\phi (\pi )(\overline {x}))$
.
In Theorem 6.1 the first two clauses define the property EPPA for
![]() ${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
and (i)–(iii) together give the definition of coherent EPPA. Before closing this section we show that these properties are equivalent to the semiproperness of the continuous signature
${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
and (i)–(iii) together give the definition of coherent EPPA. Before closing this section we show that these properties are equivalent to the semiproperness of the continuous signature
![]() $\mathcal {L}$
. Note, however, that we assume a slightly stronger background condition than before for the continuous signature
$\mathcal {L}$
. Note, however, that we assume a slightly stronger background condition than before for the continuous signature
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Theorem 6.2. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are strictly increasing. The following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are strictly increasing. The following are equivalent:
-
(1)
 $\mathcal {L}$
is semiproper.
$\mathcal {L}$
is semiproper. -
(2)
 ${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
has the EPPA.
${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
has the EPPA. -
(3)
 ${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
has the coherent EPPA.
${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
has the coherent EPPA.
Proof (1)
![]() $\Rightarrow $
(3) by Theorem 6.1. (3)
$\Rightarrow $
(3) by Theorem 6.1. (3)
![]() $\Rightarrow $
(2) is obvious. We show (2)
$\Rightarrow $
(2) is obvious. We show (2)
![]() $\Rightarrow $
(1). For this, let
$\Rightarrow $
(1). For this, let
![]() $R\in \mathcal {L}$
be n-ary and let
$R\in \mathcal {L}$
be n-ary and let
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
We first show that
![]() $I_{R,i}$
is bounded. Toward a contradiction, assume
$I_{R,i}$
is bounded. Toward a contradiction, assume
![]() $I_{R,i}$
is unbounded, that is,
$I_{R,i}$
is unbounded, that is,
![]() $I_{R,i}=[0,+\infty )$
. Let
$I_{R,i}=[0,+\infty )$
. Let
![]() $M=\sup \{\,\mathfrak {u}_{R,i}(r)\,:\, r\geq 0\}\leq 1$
. Since
$M=\sup \{\,\mathfrak {u}_{R,i}(r)\,:\, r\geq 0\}\leq 1$
. Since
![]() $\mathfrak {u}_{R,i}$
is strictly increasing, we have
$\mathfrak {u}_{R,i}$
is strictly increasing, we have
![]() $\mathfrak {u}_{R,i}(r)<M$
for all
$\mathfrak {u}_{R,i}(r)<M$
for all
![]() $r\geq 0$
. Let
$r\geq 0$
. Let
![]() $a, b>0$
be such that
$a, b>0$
be such that
![]() $\mathfrak {u}_{R,i}(a)+\mathfrak {u}_{R,i}(b)>M$
. Let
$\mathfrak {u}_{R,i}(a)+\mathfrak {u}_{R,i}(b)>M$
. Let
![]() $\epsilon>0$
be such that
$\epsilon>0$
be such that
![]() $\epsilon < M-\mathfrak {u}_{R,i}(a+b)$
. Let
$\epsilon < M-\mathfrak {u}_{R,i}(a+b)$
. Let
![]() $\delta>0$
be sufficiently large such that
$\delta>0$
be sufficiently large such that
![]() $\mathfrak {u}_{R,i}(a+\delta +b)>M-\epsilon $
. Consider the metric space
$\mathfrak {u}_{R,i}(a+\delta +b)>M-\epsilon $
. Consider the metric space
![]() $(M, d^M)$
consisting of four points
$(M, d^M)$
consisting of four points
![]() $y, s, t, z$
on the real line where
$y, s, t, z$
on the real line where
![]() $s-y=a$
,
$s-y=a$
,
![]() $t-s=\delta $
and
$t-s=\delta $
and
![]() $z-t=b$
. For
$z-t=b$
. For
![]() $\overline {x}=(x_1,\dots , x_n)\in M^n$
, define
$\overline {x}=(x_1,\dots , x_n)\in M^n$
, define
 $$ \begin{align*}R^M(\overline{x})=\left\{\begin{array}{@{}ll} M-\epsilon, & \mbox{ if}\ x_i=y, \\ \mathfrak{u}_{R,i}(b), & \mbox{ if}\ x_i=s\ \mbox{ or}\ x_i=t, \\ 0, & \mbox{ if}\ x_i=z. \end{array}\right. \end{align*} $$
$$ \begin{align*}R^M(\overline{x})=\left\{\begin{array}{@{}ll} M-\epsilon, & \mbox{ if}\ x_i=y, \\ \mathfrak{u}_{R,i}(b), & \mbox{ if}\ x_i=s\ \mbox{ or}\ x_i=t, \\ 0, & \mbox{ if}\ x_i=z. \end{array}\right. \end{align*} $$
For all other
![]() $\tilde {R}\in \mathcal {L}$
, define
$\tilde {R}\in \mathcal {L}$
, define
![]() $\tilde {R}^M$
to be identically
$\tilde {R}^M$
to be identically
![]() $0$
. It is easy to check that this defines a finite continuous
$0$
. It is easy to check that this defines a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $p: \{s, t\}\to \{s, t\}$
be defined as
$p: \{s, t\}\to \{s, t\}$
be defined as
![]() $p(s)=t$
and
$p(s)=t$
and
![]() $p(t)=s$
. Then p is a partial isomorphism of
$p(t)=s$
. Then p is a partial isomorphism of
![]() $\mathcal {M}$
. By the EPPA, there is a finite continuous
$\mathcal {M}$
. By the EPPA, there is a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
and an automorphism f of
$\mathcal {N}$
and an automorphism f of
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
![]() $\mathcal {M}$
and f is an extension of p. Let
$\mathcal {M}$
and f is an extension of p. Let
![]() $y'=f(y)$
. Then
$y'=f(y)$
. Then
![]() $d^N(y',t)=d^N(f(y), f(s))=d^N(y,s)=d^M(y,s)=a$
. Define
$d^N(y',t)=d^N(f(y), f(s))=d^N(y,s)=d^M(y,s)=a$
. Define
![]() $\overline {x}^0$
,
$\overline {x}^0$
,
![]() $\overline {x}^1$
,
$\overline {x}^1$
,
![]() $\overline {x}^2$
as follows.
$\overline {x}^2$
as follows.
 $$ \begin{align*}\begin{array}{ccc} x^0_j=\left\{\begin{array}{@{}ll} y, & \mbox{ if}\ j=i, \\ s, & \mbox{ if}\ j\neq i, \end{array}\right. & x^1_j=\left\{\begin{array}{@{}ll} y', & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i, \end{array}\right. & x^2_j=\left\{\begin{array}{@{}ll} z, & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i. \end{array}\right. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} x^0_j=\left\{\begin{array}{@{}ll} y, & \mbox{ if}\ j=i, \\ s, & \mbox{ if}\ j\neq i, \end{array}\right. & x^1_j=\left\{\begin{array}{@{}ll} y', & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i, \end{array}\right. & x^2_j=\left\{\begin{array}{@{}ll} z, & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i. \end{array}\right. \end{array} \end{align*} $$
Then
![]() $\overline {x}^1=f(\overline {x}^0)$
and thus
$\overline {x}^1=f(\overline {x}^0)$
and thus
![]() $R^N(\overline {x}^1)=R^N(\overline {x}^0)=R^M(\overline {x}^0)= M-\epsilon $
. It follows that
$R^N(\overline {x}^1)=R^N(\overline {x}^0)=R^M(\overline {x}^0)= M-\epsilon $
. It follows that
contradicting our choice of
![]() $\epsilon $
.
$\epsilon $
.
Next we show that
![]() $\mathfrak {u}_{R,i}$
is superadditive on
$\mathfrak {u}_{R,i}$
is superadditive on
![]() $I_{R,i}$
. For this we use a construction similar to the above one. Let
$I_{R,i}$
. For this we use a construction similar to the above one. Let
![]() $a, b>0$
be such that
$a, b>0$
be such that
![]() $a+b\in I_{R,i}$
. Let
$a+b\in I_{R,i}$
. Let
![]() $\delta> \sup I_{R,i}$
. Consider the metric space
$\delta> \sup I_{R,i}$
. Consider the metric space
![]() $(M, d^M)$
consisting of four points
$(M, d^M)$
consisting of four points
![]() $y, s, t, z$
on the real line where
$y, s, t, z$
on the real line where
![]() $s-y=a$
,
$s-y=a$
,
![]() $t-s=\delta $
, and
$t-s=\delta $
, and
![]() $z-t=b$
. For
$z-t=b$
. For
![]() $\overline {x}=(x_1,\dots , x_n)\in M^n$
, define
$\overline {x}=(x_1,\dots , x_n)\in M^n$
, define
 $$ \begin{align*}R^M(\overline{x})=\left\{\begin{array}{@{}ll} \mbox{min}\{1,\mathfrak{u}_{R,i}(a)+\mathfrak{u}_{R,i}(b)\}, & \mbox{ if}\ x_i=y, \\ \mathfrak{u}_{R,i}(b), & \mbox{ if}\ x_i=s\ \mbox{ or}\ x_i=t, \\ 0, & \mbox{ if}\ x_i=z. \end{array}\right. \end{align*} $$
$$ \begin{align*}R^M(\overline{x})=\left\{\begin{array}{@{}ll} \mbox{min}\{1,\mathfrak{u}_{R,i}(a)+\mathfrak{u}_{R,i}(b)\}, & \mbox{ if}\ x_i=y, \\ \mathfrak{u}_{R,i}(b), & \mbox{ if}\ x_i=s\ \mbox{ or}\ x_i=t, \\ 0, & \mbox{ if}\ x_i=z. \end{array}\right. \end{align*} $$
For all other
![]() $\tilde {R}\in \mathcal {L}$
, define
$\tilde {R}\in \mathcal {L}$
, define
![]() $\tilde {R}^M$
to be identically
$\tilde {R}^M$
to be identically
![]() $0$
. It is easy to check that this defines a finite continuous
$0$
. It is easy to check that this defines a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $p: \{s, t\}\to \{s, t\}$
be defined as
$p: \{s, t\}\to \{s, t\}$
be defined as
![]() $p(s)=t$
and
$p(s)=t$
and
![]() $p(t)=s$
. Then p is a partial isomorphism of
$p(t)=s$
. Then p is a partial isomorphism of
![]() $\mathcal {M}$
. By the EPPA, there is a finite continuous
$\mathcal {M}$
. By the EPPA, there is a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
and an automorphism f of
$\mathcal {N}$
and an automorphism f of
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
![]() $\mathcal {M}$
and f is an extension of p. Let
$\mathcal {M}$
and f is an extension of p. Let
![]() $y'=f(y)$
. Then
$y'=f(y)$
. Then
![]() $d^N(y',t)=d^N(f(y), f(s))=d^N(y,s)=d^M(y,s)=a$
. Define
$d^N(y',t)=d^N(f(y), f(s))=d^N(y,s)=d^M(y,s)=a$
. Define
![]() $\overline {x}^0$
,
$\overline {x}^0$
,
![]() $\overline {x}^1$
,
$\overline {x}^1$
,
![]() $\overline {x}^2$
as before.
$\overline {x}^2$
as before.
 $$ \begin{align*}\begin{array}{ccc} x^0_j=\left\{\begin{array}{@{}ll} y, & \mbox{ if}\ j=i, \\ s, & \mbox{ if}\ j\neq i, \end{array}\right. & x^1_j=\left\{\begin{array}{@{}ll} y', & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i, \end{array}\right. & x^2_j=\left\{\begin{array}{@{}ll} z, & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i. \end{array}\right. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} x^0_j=\left\{\begin{array}{@{}ll} y, & \mbox{ if}\ j=i, \\ s, & \mbox{ if}\ j\neq i, \end{array}\right. & x^1_j=\left\{\begin{array}{@{}ll} y', & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i, \end{array}\right. & x^2_j=\left\{\begin{array}{@{}ll} z, & \mbox{ if}\ j=i, \\ t, & \mbox{ if}\ j\neq i. \end{array}\right. \end{array} \end{align*} $$
Then
![]() $\overline {x}^1{\kern-1pt}={\kern-1pt}f(\overline {x}^0)$
and thus
$\overline {x}^1{\kern-1pt}={\kern-1pt}f(\overline {x}^0)$
and thus
![]() $R^N(\overline {x}^1){\kern-1pt}={\kern-1pt}R^N(\overline {x}^0){\kern-1pt}={\kern-1pt}R^M(\overline {x}^0){\kern-1pt}={\kern-1pt} \mbox {min}\{1,\mathfrak {u}_{R,i}(a)+\mathfrak {u}_{R,i}(b)\}$
. It follows that
$R^N(\overline {x}^1){\kern-1pt}={\kern-1pt}R^N(\overline {x}^0){\kern-1pt}={\kern-1pt}R^M(\overline {x}^0){\kern-1pt}={\kern-1pt} \mbox {min}\{1,\mathfrak {u}_{R,i}(a)+\mathfrak {u}_{R,i}(b)\}$
. It follows that
 $$ \begin{align*}\mbox{min}\{1,\mathfrak{u}_{R,i}(a)+\mathfrak{u}_{R,i}(b)\} &=|R^N(\overline{x}^1)- R^N(\overline{x}^2)| \\&\leq \mathfrak{u}_{R,i}(d^N(y',z)) \\&\leq \mathfrak{u}_{R,i}(d^N(y',t)+d^N(t,z))=\mathfrak{u}_{R,i}(a+b). \end{align*} $$
$$ \begin{align*}\mbox{min}\{1,\mathfrak{u}_{R,i}(a)+\mathfrak{u}_{R,i}(b)\} &=|R^N(\overline{x}^1)- R^N(\overline{x}^2)| \\&\leq \mathfrak{u}_{R,i}(d^N(y',z)) \\&\leq \mathfrak{u}_{R,i}(d^N(y',t)+d^N(t,z))=\mathfrak{u}_{R,i}(a+b). \end{align*} $$
Since
![]() $\mathfrak {u}_{R,i}(a+b)<1$
, we have
$\mathfrak {u}_{R,i}(a+b)<1$
, we have
![]() $\mathfrak {u}_{R,i}(a)+\mathfrak {u}_{R,i}(b)\leq \mathfrak {u}_{R,i}(a+b)$
as desired.
$\mathfrak {u}_{R,i}(a)+\mathfrak {u}_{R,i}(b)\leq \mathfrak {u}_{R,i}(a+b)$
as desired.
Finally we show that if
![]() $R\in \mathcal {L}$
is n-ary with
$R\in \mathcal {L}$
is n-ary with
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1\leq i\leq n$
, then there is
$1\leq i\leq n$
, then there is
![]() $K_{R,i}>0$
such that
$K_{R,i}>0$
such that
![]() $\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
$\mathfrak {u}_{R,i}(r)=K_{R,i}r$
for all
![]() $r\in I_{R,i}$
. For this we show that
$r\in I_{R,i}$
. For this we show that
![]() $\mathfrak {u}_{R,i}$
is subadditive on
$\mathfrak {u}_{R,i}$
is subadditive on
![]() $I_{R,i}$
. Let
$I_{R,i}$
. Let
![]() $1\leq k\leq n$
be such that
$1\leq k\leq n$
be such that
![]() $k\neq i$
. Let
$k\neq i$
. Let
![]() ${a, b>0}$
be such that
${a, b>0}$
be such that
![]() $a+b\in I_{R,i}$
. Consider the metric space
$a+b\in I_{R,i}$
. Consider the metric space
![]() $(M, d^M)$
consisting of five points
$(M, d^M)$
consisting of five points
![]() $r, s, t, z, y$
, where
$r, s, t, z, y$
, where
![]() $r,s,t$
form an equilateral triangle with side length
$r,s,t$
form an equilateral triangle with side length
![]() ${a+b}$
,
${a+b}$
,
![]() $d^N(y,s)=b$
,
$d^N(y,s)=b$
,
![]() $d^N(y, t)=a$
,
$d^N(y, t)=a$
,
![]() $d^N(y, r)=\mbox {min}\{2a+b, a+2b\}$
, and
$d^N(y, r)=\mbox {min}\{2a+b, a+2b\}$
, and
![]() $d^N(z,r)=d^N(z,s)=d^N(z,t)=d^N(z,y)=\delta $
for some
$d^N(z,r)=d^N(z,s)=d^N(z,t)=d^N(z,y)=\delta $
for some
![]() $\delta>\sup I_{R,i}$
. For
$\delta>\sup I_{R,i}$
. For
![]() $\overline {x}=(x_1,\dots , x_n)\in M^n$
, define
$\overline {x}=(x_1,\dots , x_n)\in M^n$
, define
 $$ \begin{align*}R^M(\overline{x})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R,i}(a+b), & \mbox{ if}\ x_i=r\ \mbox{ and}\ x_k=z, \\ 0, & \mbox{ otherwise.}\end{array}\right.\end{align*} $$
$$ \begin{align*}R^M(\overline{x})=\left\{\begin{array}{@{}ll} \mathfrak{u}_{R,i}(a+b), & \mbox{ if}\ x_i=r\ \mbox{ and}\ x_k=z, \\ 0, & \mbox{ otherwise.}\end{array}\right.\end{align*} $$
For all other
![]() $\tilde {R}\in \mathcal {L}$
, define
$\tilde {R}\in \mathcal {L}$
, define
![]() $\tilde {R}^M$
to be identically
$\tilde {R}^M$
to be identically
![]() $0$
. It is easy to check that this defines a finite continuous
$0$
. It is easy to check that this defines a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $p:\{r,s,t\}\to \{r,s,t\}$
be such that
$p:\{r,s,t\}\to \{r,s,t\}$
be such that
![]() $p(r)=s$
,
$p(r)=s$
,
![]() $p(s)=t$
and
$p(s)=t$
and
![]() $p(t)=r$
. Then p is a partial isomorphism of
$p(t)=r$
. Then p is a partial isomorphism of
![]() $\mathcal {M}$
. By the EPPA, we obtain a finite continuous
$\mathcal {M}$
. By the EPPA, we obtain a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
and an automorphism f of
$\mathcal {N}$
and an automorphism f of
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
![]() $\mathcal {N}$
and f is an extension of p. Let
$\mathcal {N}$
and f is an extension of p. Let
![]() $y'=f(y)\in N$
. Then
$y'=f(y)\in N$
. Then
![]() $d^N(y', r)=d^N(f(y), f(t))=d^N(y, t)=a$
and
$d^N(y', r)=d^N(f(y), f(t))=d^N(y, t)=a$
and
![]() $d^N(y', t)=d^N(f(y), f(s))=d^N(y, s)=b$
. Define
$d^N(y', t)=d^N(f(y), f(s))=d^N(y, s)=b$
. Define
![]() $\overline {x}^0$
,
$\overline {x}^0$
,
![]() $\overline {x}^1$
,
$\overline {x}^1$
,
![]() $\overline {x}^2$
as follows.
$\overline {x}^2$
as follows.
 $$ \begin{align*}\begin{array}{ccc} x^0_j=\left\{\begin{array}{@{}ll} r, & \mbox{ if}\ j=i, \\ z, & \mbox{ if}\ j\neq i, \end{array}\right. & x^1_j=\left\{\begin{array}{@{}ll} t, & \mbox{ if}\ j=i, \\ z, & \mbox{ if}\ j\neq i, \end{array}\right. & x^2_j=\left\{\begin{array}{@{}ll} y', & \mbox{ if}\ j=i, \\ z, & \mbox{ if}\ j\neq i. \end{array}\right. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} x^0_j=\left\{\begin{array}{@{}ll} r, & \mbox{ if}\ j=i, \\ z, & \mbox{ if}\ j\neq i, \end{array}\right. & x^1_j=\left\{\begin{array}{@{}ll} t, & \mbox{ if}\ j=i, \\ z, & \mbox{ if}\ j\neq i, \end{array}\right. & x^2_j=\left\{\begin{array}{@{}ll} y', & \mbox{ if}\ j=i, \\ z, & \mbox{ if}\ j\neq i. \end{array}\right. \end{array} \end{align*} $$
Then
 $$ \begin{align*}\mathfrak{u}_{R,i}(a+b)&=|R^N(\overline{x}^0)-R^N(\overline{x}^1)| \\&\leq |R^N(\overline{x}^0)-R^N(\overline{x}^2)|+|R^N(\overline{x}^2)-R^N(\overline{x}^1)| \\&\leq \mathfrak{u}_{R,i}(d^N(r,y'))+\mathfrak{u}_{R,i}(d^N(y',t)) =\mathfrak{u}_{R,i}(a)+\mathfrak{u}_{R,i}(b).\\[-33pt] \end{align*} $$
$$ \begin{align*}\mathfrak{u}_{R,i}(a+b)&=|R^N(\overline{x}^0)-R^N(\overline{x}^1)| \\&\leq |R^N(\overline{x}^0)-R^N(\overline{x}^2)|+|R^N(\overline{x}^2)-R^N(\overline{x}^1)| \\&\leq \mathfrak{u}_{R,i}(d^N(r,y'))+\mathfrak{u}_{R,i}(d^N(y',t)) =\mathfrak{u}_{R,i}(a)+\mathfrak{u}_{R,i}(b).\\[-33pt] \end{align*} $$
7. Actions by automorphisms on continuous structures
In this section we prove that the actions by automorphisms on finite continuous
![]() $\mathcal {L}$
-structures form a Fraïssé class for any semiproper continuous signature
$\mathcal {L}$
-structures form a Fraïssé class for any semiproper continuous signature
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Definition 7.1. Let
![]() $\mathcal {L}$
be a semiproper continuous signature. Let
$\mathcal {L}$
be a semiproper continuous signature. Let
![]() $\mathcal {C}_{\mathcal {L}}$
be the class of all actions
$\mathcal {C}_{\mathcal {L}}$
be the class of all actions
![]() $\Gamma \curvearrowright \mathcal {M}$
such that:
$\Gamma \curvearrowright \mathcal {M}$
such that:
-
•
 $\mathcal {M}$
is a finite continuous
$\mathcal {M}$
is a finite continuous
 $\mathcal {L}$
-structure,
$\mathcal {L}$
-structure, -
•
 $\Gamma $
is a finite group, and
$\Gamma $
is a finite group, and -
•
 $\Gamma \curvearrowright \mathcal {M}$
is an action by automorphisms.
$\Gamma \curvearrowright \mathcal {M}$
is an action by automorphisms.
Our objective is to show that
![]() $\mathcal {C}_{\mathcal {L}}$
is a Fraïssé class. By this we mean that
$\mathcal {C}_{\mathcal {L}}$
is a Fraïssé class. By this we mean that
![]() $\mathcal {C}_{\mathcal {L}}$
has the hereditary property, the joint embedding property, and the amalgamation property. They are defined below.
$\mathcal {C}_{\mathcal {L}}$
has the hereditary property, the joint embedding property, and the amalgamation property. They are defined below.
Definition 7.2. Let
![]() $\mathcal {L}$
be a semiproper continuous signature. Let
$\mathcal {L}$
be a semiproper continuous signature. Let
![]() $\Lambda , \Gamma $
be groups,
$\Lambda , \Gamma $
be groups,
![]() $\mathcal {M}, \mathcal {N}$
be continuous
$\mathcal {M}, \mathcal {N}$
be continuous
![]() $\mathcal {L}$
-pre-structures, and
$\mathcal {L}$
-pre-structures, and
![]() $\tau :\Lambda \curvearrowright \mathcal {M}$
and
$\tau :\Lambda \curvearrowright \mathcal {M}$
and
![]() $\pi :\Gamma \curvearrowright \mathcal {N}$
be actions by automorphisms.
$\pi :\Gamma \curvearrowright \mathcal {N}$
be actions by automorphisms.
-
(1) An embedding from
 $\tau $
into
$\tau $
into
 $\pi $
is a pair
$\pi $
is a pair
 $(e, f)$
where e is a group isomorphic embedding from
$(e, f)$
where e is a group isomorphic embedding from
 $\Lambda $
into
$\Lambda $
into
 $\Gamma $
and f is an embedding from
$\Gamma $
and f is an embedding from
 $\mathcal {M}$
to
$\mathcal {M}$
to
 $\mathcal {N}$
as continuous
$\mathcal {N}$
as continuous
 $\mathcal {L}$
-pre-structures such that for all
$\mathcal {L}$
-pre-structures such that for all
 $g\in \Lambda $
and
$g\in \Lambda $
and
 $x\in M$
,
$x\in M$
,
 $e(g)\cdot _{\pi }f(x)=f(g\cdot _{\tau }x)$
.
$e(g)\cdot _{\pi }f(x)=f(g\cdot _{\tau }x)$
. -
(2) We say that
 $\mathcal {C}_{\mathcal {L}}$
has the hereditary property (HP) if for any
$\mathcal {C}_{\mathcal {L}}$
has the hereditary property (HP) if for any
 $\tau :\Lambda \curvearrowright \mathcal {M}$
and
$\tau :\Lambda \curvearrowright \mathcal {M}$
and
 $\pi :\Gamma \curvearrowright \mathcal {N}$
, whenever
$\pi :\Gamma \curvearrowright \mathcal {N}$
, whenever
 $\pi \in \mathcal {C}_{\mathcal {L}}$
and there is an embedding from
$\pi \in \mathcal {C}_{\mathcal {L}}$
and there is an embedding from
 $\tau $
into
$\tau $
into
 $\pi $
, then
$\pi $
, then
 $\tau \in \mathcal {C}_{\mathcal {L}}$
.
$\tau \in \mathcal {C}_{\mathcal {L}}$
. -
(3) We say that
 $\mathcal {C}_{\mathcal {L}}$
has the joint embedding property (JEP) if given any
$\mathcal {C}_{\mathcal {L}}$
has the joint embedding property (JEP) if given any
 $\tau ,\pi \in \mathcal {C}_{\mathcal {L}}$
there is a
$\tau ,\pi \in \mathcal {C}_{\mathcal {L}}$
there is a
 $\kappa \in \mathcal {C}_{\mathcal {L}}$
and embeddings from
$\kappa \in \mathcal {C}_{\mathcal {L}}$
and embeddings from
 $\tau $
into
$\tau $
into
 $\kappa $
and from
$\kappa $
and from
 $\pi $
into
$\pi $
into
 $\kappa $
.
$\kappa $
. -
(4) We say that
 $\mathcal {C}_{\mathcal {L}}$
has the amalgamation property (AP) if given any
$\mathcal {C}_{\mathcal {L}}$
has the amalgamation property (AP) if given any
 $\mu , \tau , \pi \in \mathcal {C}_{\mathcal {L}}$
and embeddings
$\mu , \tau , \pi \in \mathcal {C}_{\mathcal {L}}$
and embeddings
 $(e,f)$
from
$(e,f)$
from
 $\mu $
into
$\mu $
into
 $\tau $
and
$\tau $
and
 $(p,q)$
from
$(p,q)$
from
 $\mu $
into
$\mu $
into
 $\pi $
, there exist a
$\pi $
, there exist a
 $\kappa \in \mathcal {C}_{\mathcal {L}}$
and embeddings
$\kappa \in \mathcal {C}_{\mathcal {L}}$
and embeddings
 $(g,h)$
from
$(g,h)$
from
 $\tau $
into
$\tau $
into
 $\kappa $
and
$\kappa $
and
 $(r,s)$
from
$(r,s)$
from
 $\pi $
into
$\pi $
into
 $\kappa $
such that
$\kappa $
such that  $$ \begin{align*}g\circ e=r\circ p \mbox{ and } h\circ f=s\circ q.\end{align*} $$
$$ \begin{align*}g\circ e=r\circ p \mbox{ and } h\circ f=s\circ q.\end{align*} $$
Our proof will follow the general line of arguments for Theorems 3.9 and 4.8 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]. Two key ingredients of the proof are analogs of some results of Rosendal (Lemma 16 of [Reference Rosendal15] and Theorem 7 of [Reference Rosendal14], also cf. Lemma 4.7 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8], Theorem 4.6 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8], and Theorem 3.3 of [Reference Etedadialiabadi and Gao7]). We develop these results first.
7.1. Extensions of actions by automorphisms
In this subsection we generalize a lemma of Rosendal (Lemma 16 of [Reference Rosendal15]; also cf. Lemma 4.7 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]) to finite continuous
![]() $\mathcal {L}$
-structures for a semiproper continuous signature
$\mathcal {L}$
-structures for a semiproper continuous signature
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
We will prove a more general result with the stronger assumption that
![]() $\mathcal {L}$
is a proper continuous signature. The same proof will give the desired result for semiproper
$\mathcal {L}$
is a proper continuous signature. The same proof will give the desired result for semiproper
![]() $\mathcal {L}$
. So, for the time being let us assume
$\mathcal {L}$
. So, for the time being let us assume
![]() $\mathcal {L}$
is proper.
$\mathcal {L}$
is proper.
Assume
![]() $\Gamma $
is a group,
$\Gamma $
is a group,
![]() $\Lambda \leq \Gamma $
is a subgroup,
$\Lambda \leq \Gamma $
is a subgroup,
![]() $\mathcal {M}\subseteq \mathcal {N}$
are continuous
$\mathcal {M}\subseteq \mathcal {N}$
are continuous
![]() $\mathcal {L}$
-pre-structures, and
$\mathcal {L}$
-pre-structures, and
![]() $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
![]() $\Lambda \curvearrowright \mathcal {N}$
are compatible actions by automorphisms.
$\Lambda \curvearrowright \mathcal {N}$
are compatible actions by automorphisms.
Define a pseudo-metric
![]() $\partial $
on
$\partial $
on
![]() $N\times \Gamma $
by
$N\times \Gamma $
by
 $$ \begin{align*} & \partial((y_1, g_1), (y_2, g_2)) \\& \quad =\left\{\begin{array}{@{}l} d^N(g_2^{-1}g_1\cdot y_1, y_2), \ \ \ \ \ \ \ \mbox{ if either}\ y_1, y_2\in M \mbox{ or}\ g_2^{-1}g_1\in \Lambda, \\ \inf_{x\in M}\{d^N(y_1, g_1^{-1}\cdot x)+d^N(y_2, g_2^{-1}\cdot x)\}, \ \ \ \ \ \ \ \mbox{ otherwise.} \end{array}\right. \end{align*} $$
$$ \begin{align*} & \partial((y_1, g_1), (y_2, g_2)) \\& \quad =\left\{\begin{array}{@{}l} d^N(g_2^{-1}g_1\cdot y_1, y_2), \ \ \ \ \ \ \ \mbox{ if either}\ y_1, y_2\in M \mbox{ or}\ g_2^{-1}g_1\in \Lambda, \\ \inf_{x\in M}\{d^N(y_1, g_1^{-1}\cdot x)+d^N(y_2, g_2^{-1}\cdot x)\}, \ \ \ \ \ \ \ \mbox{ otherwise.} \end{array}\right. \end{align*} $$
Then
![]() $\partial $
is a pseudo-metric on
$\partial $
is a pseudo-metric on
![]() $N\times \Gamma $
and for all
$N\times \Gamma $
and for all
![]() $(y_1, g_1), (y_2, g_2)\in N\times \Gamma $
,
$(y_1, g_1), (y_2, g_2)\in N\times \Gamma $
,
Define an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $N\times \Gamma $
by
$N\times \Gamma $
by
Then
![]() $(y_1, g_1)\sim (y_2, g_2)$
iff
$(y_1, g_1)\sim (y_2, g_2)$
iff
Let
![]() $[y, g]$
denote the
$[y, g]$
denote the
![]() $\sim $
-equivalence class of
$\sim $
-equivalence class of
![]() $(y, g)$
. Let
$(y, g)$
. Let
and let
Then
![]() $d^P$
is a metric on P.
$d^P$
is a metric on P.
Let
![]() $\varphi : N\to P$
be defined as
$\varphi : N\to P$
be defined as
![]() $\varphi (y)=[y,1]$
. Then
$\varphi (y)=[y,1]$
. Then
![]() $\varphi $
is an isometric embedding from
$\varphi $
is an isometric embedding from
![]() $(N,d^N)$
into
$(N,d^N)$
into
![]() $(P, d^P)$
, since
$(P, d^P)$
, since
for any
![]() $y_1, y_2\in N$
.
$y_1, y_2\in N$
.
Define
![]() $\Gamma \curvearrowright P$
by
$\Gamma \curvearrowright P$
by
for
![]() $g, h\in \Gamma $
and
$g, h\in \Gamma $
and
![]() $y\in N$
. It is easy to see that this is well defined.
$y\in N$
. It is easy to see that this is well defined.
Now suppose
![]() $R\in \mathcal {L}$
is an n-ary relation symbol. Define
$R\in \mathcal {L}$
is an n-ary relation symbol. Define
if
![]() $z_1, \dots , z_n\in N$
,
$z_1, \dots , z_n\in N$
,
![]() $g\in \Gamma $
, and
$g\in \Gamma $
, and
Thus
 $$ \begin{align*}\begin{array}{c} [y_1, g_1], \dots, [y_1, g_n]\in {\mathrm{dom}}(R^P)\iff \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \exists g\in \Gamma, z_1, \dots, z_n\in N\ \bigwedge_{i=1}^n [y_i, g_i]=[z_i, g]. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{c} [y_1, g_1], \dots, [y_1, g_n]\in {\mathrm{dom}}(R^P)\iff \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \exists g\in \Gamma, z_1, \dots, z_n\in N\ \bigwedge_{i=1}^n [y_i, g_i]=[z_i, g]. \end{array}\end{align*} $$
We verify that
![]() $R^P$
is well defined on its domain. For this let
$R^P$
is well defined on its domain. For this let
Suppose
![]() $z_1, \dots , z_n, z_1', \dots , z_n'\in N$
and
$z_1, \dots , z_n, z_1', \dots , z_n'\in N$
and
![]() $g, g'\in \Gamma $
such that for all
$g, g'\in \Gamma $
such that for all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
We need to show that
![]() $R^N(z_1, \dots , z_n)=R^N(z_1',\dots , z_n')$
. Note that we have
$R^N(z_1, \dots , z_n)=R^N(z_1',\dots , z_n')$
. Note that we have
![]() ${g^{-1}g'\cdot z_i'=z_i}$
for all
${g^{-1}g'\cdot z_i'=z_i}$
for all
![]() $1\leq i\leq n$
, and thus
$1\leq i\leq n$
, and thus
We also note that
![]() ${\mathrm {dom}}(R^P)$
is invariant under the
${\mathrm {dom}}(R^P)$
is invariant under the
![]() $\Gamma $
action. That is, if
$\Gamma $
action. That is, if
![]() $[\overline {y}, h]\in {\mathrm {dom}}(R^P)$
and
$[\overline {y}, h]\in {\mathrm {dom}}(R^P)$
and
![]() $g\in \Gamma $
then
$g\in \Gamma $
then
and
Lemma 7.3. For any
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^P$
on
$R^P$
on
![]() ${\mathrm {dom}}(R^P)$
is
${\mathrm {dom}}(R^P)$
is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $d^P_R$
.
$d^P_R$
.
Proof We first consider unary
![]() $R\in \mathcal {L}$
. For any
$R\in \mathcal {L}$
. For any
![]() $[y_1, g_1], [y_2, g_2]\in P$
, if
$[y_1, g_1], [y_2, g_2]\in P$
, if
![]() $y_1, y_2\in M$
or
$y_1, y_2\in M$
or
![]() $g_2^{-1}g_1\in \Lambda $
then
$g_2^{-1}g_1\in \Lambda $
then
 $$ \begin{align*} &|R^P([y_1, g_1])-R^P([y_2, g_2])| =|R^N(g_2^{-1}g_1\cdot y_1)-R^N(y_2)| \\&\quad\leq \mathfrak{u}_{R,1}(d^N(g_2^{-1}g_1\cdot y_1, y_2))=\mathfrak{u}_{R,1}(d^P([y_1, g_1], [y_2, g_2])). \end{align*} $$
$$ \begin{align*} &|R^P([y_1, g_1])-R^P([y_2, g_2])| =|R^N(g_2^{-1}g_1\cdot y_1)-R^N(y_2)| \\&\quad\leq \mathfrak{u}_{R,1}(d^N(g_2^{-1}g_1\cdot y_1, y_2))=\mathfrak{u}_{R,1}(d^P([y_1, g_1], [y_2, g_2])). \end{align*} $$
Otherwise, for any
![]() $x\in M$
,
$x\in M$
,
 $$ \begin{align*}&|R^P([y_1, g_1])-R^P([y_2, g_2])| =|R^N(y_1)-R^N(y_2)| \\&\quad \leq |R^N(y_1)-R^N(g_1^{-1}\cdot x)|+|R^N(g_2^{-1}\cdot x)-R^N(y_2)|\\&\quad \leq \mathfrak{u}_{R,1}(d^N(y_1, g_1^{-1}\cdot x))+\mathfrak{u}_{R,1}(d^N(y_2, g_2^{-1}\cdot x)) \\&\quad \leq \mathfrak{u}_{R,1}(d^N(y_1, g_1^{-1}\cdot x)+d^N(y_2, g_2^{-1}\cdot x)) \end{align*} $$
$$ \begin{align*}&|R^P([y_1, g_1])-R^P([y_2, g_2])| =|R^N(y_1)-R^N(y_2)| \\&\quad \leq |R^N(y_1)-R^N(g_1^{-1}\cdot x)|+|R^N(g_2^{-1}\cdot x)-R^N(y_2)|\\&\quad \leq \mathfrak{u}_{R,1}(d^N(y_1, g_1^{-1}\cdot x))+\mathfrak{u}_{R,1}(d^N(y_2, g_2^{-1}\cdot x)) \\&\quad \leq \mathfrak{u}_{R,1}(d^N(y_1, g_1^{-1}\cdot x)+d^N(y_2, g_2^{-1}\cdot x)) \end{align*} $$
if
![]() $\mathfrak {u}_{R,1}(d^N(y_1, g_1^{-1}\cdot x)+d^N(y_2, g_2^{-1}\cdot x))<1$
, and otherwise we have nonetheless
$\mathfrak {u}_{R,1}(d^N(y_1, g_1^{-1}\cdot x)+d^N(y_2, g_2^{-1}\cdot x))<1$
, and otherwise we have nonetheless
Taking the infimum of the right-hand side over
![]() $x\in M$
, and using the upper semicontinuity of
$x\in M$
, and using the upper semicontinuity of
![]() $\mathfrak {u}_{R,1}$
, we get that
$\mathfrak {u}_{R,1}$
, we get that
Thus (UCℒ
) holds for
![]() $R^P$
. It follows that for any
$R^P$
. It follows that for any
![]() $[y_1, g_1], [y_2, g_2]\in P$
,
$[y_1, g_1], [y_2, g_2]\in P$
,
Next we consider n-ary
![]() $R\in \mathcal {L}$
where
$R\in \mathcal {L}$
where
![]() $n\geq 2$
. Let
$n\geq 2$
. Let
![]() $y_1, \dots , y_n, z_1, \dots , z_n\in N$
and
$y_1, \dots , y_n, z_1, \dots , z_n\in N$
and
![]() $g, h\in \Gamma $
. If
$g, h\in \Gamma $
. If
![]() $h^{-1}g\in \Lambda $
or
$h^{-1}g\in \Lambda $
or
![]() $y_1, \dots , y_n, z_1, \dots , z_n\in M$
, then
$y_1, \dots , y_n, z_1, \dots , z_n\in M$
, then
 $$ \begin{align*} &|R^P([y_1, g], \dots, [y_n, g])-R^P([z_1, h],\dots, [z_n, h])| \\&\quad=|R^N(h^{-1}g\cdot y_1, \dots, h^{-1}g\cdot y_n)-R^N(z_1,\dots, z_n)| \\&\quad\leq d^N_R(h^{-1}g\cdot \overline{y}, \overline{z})=d^P_R([\overline{y}, g], [\overline{z}, h]). \end{align*} $$
$$ \begin{align*} &|R^P([y_1, g], \dots, [y_n, g])-R^P([z_1, h],\dots, [z_n, h])| \\&\quad=|R^N(h^{-1}g\cdot y_1, \dots, h^{-1}g\cdot y_n)-R^N(z_1,\dots, z_n)| \\&\quad\leq d^N_R(h^{-1}g\cdot \overline{y}, \overline{z})=d^P_R([\overline{y}, g], [\overline{z}, h]). \end{align*} $$
Otherwise, for any
![]() $\overline {x}\in M^n$
, we have
$\overline {x}\in M^n$
, we have
 $$ \begin{align*}&|R^P([y_1, g], \dots, [y_n, g])-R^P([z_1, h],\dots, [z_n, h])| \\&\quad\leq |R^N(y_1,\dots, y_n)-R^N(g^{-1}\cdot x_1, \dots, g^{-1}\cdot x_n)|+\\& |R^N(h^{-1}\cdot x_1, \dots, h^{-1}\cdot x_n)-R^N(z_1,\dots, z_n)| \\&\quad \leq \displaystyle\sum_{i=1}^n K_{R,i}d^N(y_i, g^{-1}\cdot x_i)+K_{R,i}d^N(z_i, h^{-1}\cdot x_i) \\& \quad = \displaystyle\sum_{i=1}^n K_{R,i}(d^N(y_i, g^{-1}\cdot x_i)+d^N(z_i, h^{-1}\cdot x_i)). \end{align*} $$
$$ \begin{align*}&|R^P([y_1, g], \dots, [y_n, g])-R^P([z_1, h],\dots, [z_n, h])| \\&\quad\leq |R^N(y_1,\dots, y_n)-R^N(g^{-1}\cdot x_1, \dots, g^{-1}\cdot x_n)|+\\& |R^N(h^{-1}\cdot x_1, \dots, h^{-1}\cdot x_n)-R^N(z_1,\dots, z_n)| \\&\quad \leq \displaystyle\sum_{i=1}^n K_{R,i}d^N(y_i, g^{-1}\cdot x_i)+K_{R,i}d^N(z_i, h^{-1}\cdot x_i) \\& \quad = \displaystyle\sum_{i=1}^n K_{R,i}(d^N(y_i, g^{-1}\cdot x_i)+d^N(z_i, h^{-1}\cdot x_i)). \end{align*} $$
Taking the infimum of the right-hand side over all
![]() $\overline {x}\in M$
, we get
$\overline {x}\in M$
, we get
Here we use the fact that if
![]() $y_i, z_i\in M$
then we also have
$y_i, z_i\in M$
then we also have
Thus
![]() $\mathcal {P}=(P, d^P, (R^P)_{R\in \mathcal {L}})$
is a partially defined continuous
$\mathcal {P}=(P, d^P, (R^P)_{R\in \mathcal {L}})$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure. We define a conservative extension
$\mathcal {L}$
-pre-structure. We define a conservative extension
![]() $\mathcal {Q}$
of
$\mathcal {Q}$
of
![]() $\mathcal {P}$
with an action
$\mathcal {P}$
with an action
![]() $\Gamma \curvearrowright \mathcal {Q}$
. Let
$\Gamma \curvearrowright \mathcal {Q}$
. Let
![]() $(Q, d^Q)=(P, d^P)$
. For any n-ary
$(Q, d^Q)=(P, d^P)$
. For any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {w}\in Q^n$
, define
$\overline {w}\in Q^n$
, define
Then for any
![]() $g\in \Gamma $
,
$g\in \Gamma $
,
 $$ \begin{align*} R^Q(g\cdot \overline{w})&=\max\{0, \sup\{R^P(g\cdot\overline{z})-d^P_R(g\cdot\overline{w}, g\cdot\overline{z})\,:\, \overline{z}\in {\mathrm{dom}}(R^P)\} \\&=\max\{0,\sup\{ R^P(\overline{z})-d^P_R(\overline{w},\overline{z})\,:\, \overline{z}\in {\mathrm{dom}}(R^P)\} \\&= R^Q(\overline{w}). \end{align*} $$
$$ \begin{align*} R^Q(g\cdot \overline{w})&=\max\{0, \sup\{R^P(g\cdot\overline{z})-d^P_R(g\cdot\overline{w}, g\cdot\overline{z})\,:\, \overline{z}\in {\mathrm{dom}}(R^P)\} \\&=\max\{0,\sup\{ R^P(\overline{z})-d^P_R(\overline{w},\overline{z})\,:\, \overline{z}\in {\mathrm{dom}}(R^P)\} \\&= R^Q(\overline{w}). \end{align*} $$
We show that
![]() $\mathcal {Q}$
is a continuous
$\mathcal {Q}$
is a continuous
![]() $\mathcal {L}$
-pre-structure, i.e., (UCℒ
) holds for
$\mathcal {L}$
-pre-structure, i.e., (UCℒ
) holds for
![]() $\mathcal {Q}$
. For unary
$\mathcal {Q}$
. For unary
![]() $R\in \mathcal {L}$
there is nothing to prove since all
$R\in \mathcal {L}$
there is nothing to prove since all
![]() $[y,g]\in {\mathrm {dom}}(R^P)$
and we have Lemma 7.3. For
$[y,g]\in {\mathrm {dom}}(R^P)$
and we have Lemma 7.3. For
![]() $n\geq 2$
and n-ary
$n\geq 2$
and n-ary
![]() $R\in \mathcal {L}$
the proof is identical to the proof of Lemma 3.7.
$R\in \mathcal {L}$
the proof is identical to the proof of Lemma 3.7.
Thus we obtain an extension
![]() $\mathcal {Q}$
of
$\mathcal {Q}$
of
![]() $\mathcal {N}$
with an action
$\mathcal {N}$
with an action
![]() $\Gamma \curvearrowright \mathcal {Q}$
. It is clear that the action
$\Gamma \curvearrowright \mathcal {Q}$
. It is clear that the action
![]() $\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
$\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
![]() $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
![]() $\Lambda \curvearrowright \mathcal {N}$
.
$\Lambda \curvearrowright \mathcal {N}$
.
Thus we have proved the following.
Theorem 7.4. Let
![]() $\mathcal {L}$
be a proper continuous signature. Let
$\mathcal {L}$
be a proper continuous signature. Let
![]() $\Gamma $
be a group,
$\Gamma $
be a group,
![]() $\Lambda \leq \Gamma $
be a subgroup,
$\Lambda \leq \Gamma $
be a subgroup,
![]() $\mathcal {M}\subseteq \mathcal {N}$
be continuous
$\mathcal {M}\subseteq \mathcal {N}$
be continuous
![]() $\mathcal {L}$
-pre-structures, and
$\mathcal {L}$
-pre-structures, and
![]() $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
![]() $\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a continuous
$\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {Q}$
and an action
$\mathcal {Q}$
and an action
![]() $\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
$\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
![]() $\mathcal {Q}$
is an extension of
$\mathcal {Q}$
is an extension of
![]() $\mathcal {N}$
, the action
$\mathcal {N}$
, the action
![]() $\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
$\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
![]() $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
![]() $\Lambda \curvearrowright \mathcal {N}$
.
$\Lambda \curvearrowright \mathcal {N}$
.
Moreover, if
![]() $\mathcal {L}$
is semiproper and
$\mathcal {L}$
is semiproper and
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\Gamma $
are finite, then the same holds with a finite
$\Gamma $
are finite, then the same holds with a finite
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Before closing this subsection we note that the above extension properties are in fact equivalent to the semiproperness and the properness of
![]() $\mathcal {L}$
, respectively. Here again we assume the slightly strong background condition for the continuous signature
$\mathcal {L}$
, respectively. Here again we assume the slightly strong background condition for the continuous signature
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Theorem 7.5. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are strictly increasing. The following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are strictly increasing. The following are equivalent:
-
(i)
 $\mathcal {L}$
is semiproper.
$\mathcal {L}$
is semiproper. -
(ii) Let
 $\Gamma $
be a group,
$\Gamma $
be a group,
 $\Lambda \leq \Gamma $
be a subgroup,
$\Lambda \leq \Gamma $
be a subgroup,
 $\mathcal {M}\subseteq \mathcal {N}$
be finite continuous
$\mathcal {M}\subseteq \mathcal {N}$
be finite continuous
 $\mathcal {L}$
-structures, and
$\mathcal {L}$
-structures, and
 $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
 $\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a finite continuous
$\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a finite continuous
 $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
 $\mathcal {Q}$
and an action
$\mathcal {Q}$
and an action
 $\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
$\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
 $\mathcal {Q}$
is an extension of
$\mathcal {Q}$
is an extension of
 $\mathcal {N}$
, the action
$\mathcal {N}$
, the action
 $\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
$\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
 $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
 $\Lambda \curvearrowright \mathcal {N}$
.
$\Lambda \curvearrowright \mathcal {N}$
. -
(iii) Let
 $\Gamma $
be a group,
$\Gamma $
be a group,
 $\Lambda \leq \Gamma $
be a subgroup,
$\Lambda \leq \Gamma $
be a subgroup,
 $\mathcal {M}\subseteq \mathcal {N}$
be finite continuous
$\mathcal {M}\subseteq \mathcal {N}$
be finite continuous
 $\mathcal {L}$
-structures, and
$\mathcal {L}$
-structures, and
 $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
 $\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a continuous
$\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a continuous
 $\mathcal {L}$
-(pre)-structure
$\mathcal {L}$
-(pre)-structure
 $\mathcal {Q}$
and an action
$\mathcal {Q}$
and an action
 $\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
$\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
 $\mathcal {Q}$
is an extension of
$\mathcal {Q}$
is an extension of
 $\mathcal {N}$
, the action
$\mathcal {N}$
, the action
 $\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
$\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
 $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
 $\Lambda \curvearrowright \mathcal {N}$
.
$\Lambda \curvearrowright \mathcal {N}$
.
Proof (i)
![]() $\Rightarrow $
(ii) by Theorem 7.4. (ii)
$\Rightarrow $
(ii) by Theorem 7.4. (ii)
![]() $\Rightarrow $
(iii) is obvious. For (iii)
$\Rightarrow $
(iii) is obvious. For (iii)
![]() $\Rightarrow $
(i) we use the same constructions and similar arguments in the proof of (2)
$\Rightarrow $
(i) we use the same constructions and similar arguments in the proof of (2)
![]() $\Rightarrow $
(1) of Theorem 6.2.
$\Rightarrow $
(1) of Theorem 6.2.
Theorem 7.6. Let
![]() $\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are strictly increasing. The following are equivalent:
$\mathcal {L}$
be a continuous signature with only finitely many relation symbols, where all the associated moduli of continuity are strictly increasing. The following are equivalent:
-
(i)
 $\mathcal {L}$
is proper.
$\mathcal {L}$
is proper. -
(ii) Let
 $\Gamma $
be a group,
$\Gamma $
be a group,
 $\Lambda \leq \Gamma $
be a subgroup,
$\Lambda \leq \Gamma $
be a subgroup,
 $\mathcal {M}\subseteq \mathcal {N}$
be continuous
$\mathcal {M}\subseteq \mathcal {N}$
be continuous
 $\mathcal {L}$
-pre-structures, and
$\mathcal {L}$
-pre-structures, and
 $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
 $\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a continuous
$\Lambda \curvearrowright \mathcal {N}$
be compatible actions by automorphisms. Then there is a continuous
 $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
 $\mathcal {Q}$
and an action
$\mathcal {Q}$
and an action
 $\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
$\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
 $\mathcal {Q}$
is an extension of
$\mathcal {Q}$
is an extension of
 $\mathcal {N}$
, the action
$\mathcal {N}$
, the action
 $\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
$\Gamma \curvearrowright \mathcal {Q}$
is compatible with both
 $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
 $\Lambda \curvearrowright \mathcal {N}$
.
$\Lambda \curvearrowright \mathcal {N}$
.
Proof (i)
![]() $\Rightarrow $
(ii) by Theorem 7.4. For (ii)
$\Rightarrow $
(ii) by Theorem 7.4. For (ii)
![]() $\Rightarrow $
(i), we have from the implication (iii)
$\Rightarrow $
(i), we have from the implication (iii)
![]() $\Rightarrow $
(i) of Theorem 7.5 that
$\Rightarrow $
(i) of Theorem 7.5 that
![]() $\mathcal {L}$
is semiproper. It remains to show that for any unary
$\mathcal {L}$
is semiproper. It remains to show that for any unary
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $\mathfrak {u}_{R,1}$
is upper semicontinuous. For this, let a be a point of the interior of
$\mathfrak {u}_{R,1}$
is upper semicontinuous. For this, let a be a point of the interior of
![]() $I_{R,1}$
. Let
$I_{R,1}$
. Let
![]() $\delta>\sup I_{R,1}$
. Let
$\delta>\sup I_{R,1}$
. Let
![]() $(N, d^N)$
be a metric space consisting of the following points on the real line
$(N, d^N)$
be a metric space consisting of the following points on the real line
where
![]() $r-r_n=2^{-n}$
,
$r-r_n=2^{-n}$
,
![]() $y-r=\delta $
,
$y-r=\delta $
,
![]() $s_n-y=a+2^{-n}$
. Define
$s_n-y=a+2^{-n}$
. Define
![]() ${R^N(y)=\inf \{\mathfrak {u}_{R,1}(r): r{\kern-1pt}>{\kern-1pt}a\}}$
and
${R^N(y)=\inf \{\mathfrak {u}_{R,1}(r): r{\kern-1pt}>{\kern-1pt}a\}}$
and
![]() $R^N(x)=0$
for
$R^N(x)=0$
for
![]() $x\neq y$
. For all other
$x\neq y$
. For all other
![]() $\tilde {R}\in \mathcal {L}$
, define
$\tilde {R}\in \mathcal {L}$
, define
![]() $\tilde {R}^N$
to be identically
$\tilde {R}^N$
to be identically
![]() $0$
. It is easy to check that this defines a continuous
$0$
. It is easy to check that this defines a continuous
![]() $\mathcal {L}$
-pre-structure. Let
$\mathcal {L}$
-pre-structure. Let
![]() $\mathcal {M}$
be the substructure of
$\mathcal {M}$
be the substructure of
![]() $\mathcal {N}$
with
$\mathcal {N}$
with
![]() $M=\{r_1,\dots , r_n, \dots , s_1,\dots , s_n, \dots \}$
. Let
$M=\{r_1,\dots , r_n, \dots , s_1,\dots , s_n, \dots \}$
. Let
![]() $\Gamma =\langle g\rangle $
where
$\Gamma =\langle g\rangle $
where
![]() $g^2=1$
, and let
$g^2=1$
, and let
![]() $\Gamma \curvearrowright \mathcal {M}$
by
$\Gamma \curvearrowright \mathcal {M}$
by
![]() $g\cdot r_n=s_n$
and
$g\cdot r_n=s_n$
and
![]() $g\cdot s_n=r_n$
. Let
$g\cdot s_n=r_n$
. Let
![]() $\Lambda $
be the trivial group. By (ii) there is a continuous
$\Lambda $
be the trivial group. By (ii) there is a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {Q}$
and an action
$\mathcal {Q}$
and an action
![]() $\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
$\Gamma \curvearrowright \mathcal {Q}$
by automorphisms such that
![]() $\mathcal {Q}$
is an extension of
$\mathcal {Q}$
is an extension of
![]() $\mathcal {N}$
and the action
$\mathcal {N}$
and the action
![]() $\Gamma \curvearrowright \mathcal {Q}$
is compatible with
$\Gamma \curvearrowright \mathcal {Q}$
is compatible with
![]() $\Gamma \curvearrowright \mathcal {M}$
. Let
$\Gamma \curvearrowright \mathcal {M}$
. Let
![]() $s=g\cdot r\in Q$
. Then
$s=g\cdot r\in Q$
. Then
![]() $d^Q(s, s_n)=d^Q(g\cdot r, g\cdot r_n)=d^Q(r, r_n)=d^N(r, r_n)=2^{-n}$
. It follows that
$d^Q(s, s_n)=d^Q(g\cdot r, g\cdot r_n)=d^Q(r, r_n)=d^N(r, r_n)=2^{-n}$
. It follows that
![]() $d^Q(y,s)=\lim _n d^Q(y,s_n)=a$
. Also
$d^Q(y,s)=\lim _n d^Q(y,s_n)=a$
. Also
![]() $R^Q(s)=R^Q(r)=0$
. We have
$R^Q(s)=R^Q(r)=0$
. We have
7.2. Finite approximations of actions
In this section we prove a generalization of a theorem of Rosendal (Theorem 7 of [Reference Rosendal14], also cf. Theorem 3.3 of [Reference Etedadialiabadi and Gao7] and Theorems 3.7 and 4.6 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]) to continuous
![]() $\mathcal {L}$
-structures for semiproper
$\mathcal {L}$
-structures for semiproper
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
In order to state the theorem we need the definition of the HL-property of a group (cf. [Reference Herwig and Lascar10] and [Reference Etedadialiabadi and Gao7]; HL stands for Herwig–Lascar).
Definition 7.7. Let G be a group.
-
(i) Let
 $H_1, \dots , H_n\leq G$
. A left system of equations on
$H_1, \dots , H_n\leq G$
. A left system of equations on
 $H_1, \dots , H_n$
is a finite set of equations with variables
$H_1, \dots , H_n$
is a finite set of equations with variables
 $x_1,\dots , x_m$
and constants
$x_1,\dots , x_m$
and constants
 $g_1,\dots , g_\ell \in G$
such that each equation is of the form where
$g_1,\dots , g_\ell \in G$
such that each equation is of the form where $$ \begin{align*}x_iH_j=g_kH_j \mbox{ or } x_iH_j=x_rg_kH_j,\end{align*} $$
$$ \begin{align*}x_iH_j=g_kH_j \mbox{ or } x_iH_j=x_rg_kH_j,\end{align*} $$
 $1\leq i, r\leq m$
,
$1\leq i, r\leq m$
,
 $1\leq k\leq \ell $
, and
$1\leq k\leq \ell $
, and
 $1\leq j\leq n$
.
$1\leq j\leq n$
.
-
(ii) We say that G has the HL-property if for every finitely generated
 $H_1,\dots , H_n\ \leq G$
and left system of equations on
$H_1,\dots , H_n\ \leq G$
and left system of equations on
 $H_1,\dots , H_n$
that does not have a solution, there exist normal subgroups of finite index
$H_1,\dots , H_n$
that does not have a solution, there exist normal subgroups of finite index
 $N_1, \dots , N_n\unlhd G$
such that the same left system of equations on
$N_1, \dots , N_n\unlhd G$
such that the same left system of equations on
 $N_1H_1, \dots , N_nH_n$
does not have a solution.
$N_1H_1, \dots , N_nH_n$
does not have a solution.
Note that by introducing new variables we may also include equations of the form
in a left system.
Theorem 7.8. Let
![]() $\mathcal {L}$
be a semiproper continuous signature. Let
$\mathcal {L}$
be a semiproper continuous signature. Let
![]() $\Gamma $
be a countable group with the HL-property. Assume that
$\Gamma $
be a countable group with the HL-property. Assume that
![]() $\pi : \Gamma \curvearrowright \mathcal {M}$
is an action by automorphisms on a continuous
$\pi : \Gamma \curvearrowright \mathcal {M}$
is an action by automorphisms on a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {M}$
. Then for any finite
$\mathcal {M}$
. Then for any finite
![]() $A\subseteq M$
and finite
$A\subseteq M$
and finite
![]() $F\subseteq \Gamma $
there exist a finite continuous
$F\subseteq \Gamma $
there exist a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
and an action by automorphisms
$\mathcal {N}$
and an action by automorphisms
![]() $\pi ':\Gamma \curvearrowright \mathcal {N}$
such that
$\pi ':\Gamma \curvearrowright \mathcal {N}$
such that
![]() $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
![]() $\mathcal {A}$
and for all
$\mathcal {A}$
and for all
![]() $\gamma \in F$
and
$\gamma \in F$
and
![]() $a\in A$
, if
$a\in A$
, if
![]() $\gamma \cdot _{\pi }a\in A$
then we have
$\gamma \cdot _{\pi }a\in A$
then we have
![]() $\gamma \cdot _{\pi '}a=\gamma \cdot _{\pi }a$
.
$\gamma \cdot _{\pi '}a=\gamma \cdot _{\pi }a$
.
The remainder of this subsection is devoted to a proof of Theorem 7.8. Our strategy is to follow Rosendal’s proof of Theorem 7 [Reference Rosendal14] (a)
![]() $\Rightarrow $
(b) for the metric part (also cf. [Reference Etedadialiabadi and Gao6]) and then the Etedadialiabadi–Gao’s proof of Theorem 3.3 [Reference Etedadialiabadi and Gao7] (i)
$\Rightarrow $
(b) for the metric part (also cf. [Reference Etedadialiabadi and Gao6]) and then the Etedadialiabadi–Gao’s proof of Theorem 3.3 [Reference Etedadialiabadi and Gao7] (i)
![]() $\Rightarrow $
(ii) for the relations part. Rosendal’s proof uses the so-called property (RZ) or RZ-property of the group
$\Rightarrow $
(ii) for the relations part. Rosendal’s proof uses the so-called property (RZ) or RZ-property of the group
![]() $\Gamma $
, and Etedadialiabadi–Gao’s proof uses the HL-property. Since the RZ-property is implied by the HL-property, we will see that the two parts of the proof produces compatible requirements, which can be resolved by invoking the HL-property of
$\Gamma $
, and Etedadialiabadi–Gao’s proof uses the HL-property. Since the RZ-property is implied by the HL-property, we will see that the two parts of the proof produces compatible requirements, which can be resolved by invoking the HL-property of
![]() $\Gamma $
once. In fact, we remark that the proof can go through with assuming RZ-property only; however, we use the HL-property as the presentation is notationally simpler. Our application of the HL-property will give a finite partially defined continuous
$\Gamma $
once. In fact, we remark that the proof can go through with assuming RZ-property only; however, we use the HL-property as the presentation is notationally simpler. Our application of the HL-property will give a finite partially defined continuous
![]() $\mathcal {L}$
-structure, and we complete the proof by Lemma 3.7.
$\mathcal {L}$
-structure, and we complete the proof by Lemma 3.7.
Suppose a proper continuous signature
![]() $\mathcal {L}$
, a continuous
$\mathcal {L}$
, a continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
, a group
$\mathcal {M}$
, a group
![]() $\Gamma $
with the HL-property, an action by automorphism
$\Gamma $
with the HL-property, an action by automorphism
![]() $\pi : \Gamma \curvearrowright \mathcal {M}$
, and a finite
$\pi : \Gamma \curvearrowright \mathcal {M}$
, and a finite
![]() $A\subseteq M$
are given.
$A\subseteq M$
are given.
Without loss of generality we may assume that the action
![]() $\pi $
is faithful, i.e., for all
$\pi $
is faithful, i.e., for all
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $\gamma \neq 1_{\Gamma }$
, there is some
$\gamma \neq 1_{\Gamma }$
, there is some
![]() $x\in M$
such that
$x\in M$
such that
![]() $\gamma \cdot _{\pi } x\neq x$
. In the following, when there is no danger of confusion, we omit the subscript in
$\gamma \cdot _{\pi } x\neq x$
. In the following, when there is no danger of confusion, we omit the subscript in
![]() $\cdot _{\pi }$
.
$\cdot _{\pi }$
.
Let
and
 $$ \begin{align*}P=\{\delta_A\}\cup \left(\left\{\displaystyle\sum_{i=1}^m p_i\,:\, p_1,\dots, p_m\in P_A\right\}\cap [0, \delta_A]\right).\end{align*} $$
$$ \begin{align*}P=\{\delta_A\}\cup \left(\left\{\displaystyle\sum_{i=1}^m p_i\,:\, p_1,\dots, p_m\in P_A\right\}\cap [0, \delta_A]\right).\end{align*} $$
Since A is finite, P is finite.
We define a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\tilde {\mathcal {M}}$
as follows. Let
$\tilde {\mathcal {M}}$
as follows. Let
![]() $\tilde {M}=M$
and
$\tilde {M}=M$
and
 $$ \begin{align*}d^{\tilde{M}}(x, y)=\left\{\begin{array}{@{}ll} \min\{p\in P\,:\, d^M(x, y)\leq p\}, & \mbox{ if}\ d^M(x,y)\leq \delta_A, \\ \delta_A, & \mbox{ otherwise.}\end{array}\right.\end{align*} $$
$$ \begin{align*}d^{\tilde{M}}(x, y)=\left\{\begin{array}{@{}ll} \min\{p\in P\,:\, d^M(x, y)\leq p\}, & \mbox{ if}\ d^M(x,y)\leq \delta_A, \\ \delta_A, & \mbox{ otherwise.}\end{array}\right.\end{align*} $$
Then
![]() $d^{\tilde {M}}$
is a metric on M, and the action
$d^{\tilde {M}}$
is a metric on M, and the action
![]() $\pi :\Gamma \curvearrowright M$
is still an action by isometries on
$\pi :\Gamma \curvearrowright M$
is still an action by isometries on
![]() $(M, d^{\tilde {M}})$
(cf. Lemma 4 of [Reference Rosendal14]). For any
$(M, d^{\tilde {M}})$
(cf. Lemma 4 of [Reference Rosendal14]). For any
![]() $R\in \mathcal {L}$
, we define
$R\in \mathcal {L}$
, we define
![]() $R^{\tilde {M}}=R^M$
. Since
$R^{\tilde {M}}=R^M$
. Since
![]() $d^M(x,y)\leq d^{\tilde {M}}(x,y)$
for any
$d^M(x,y)\leq d^{\tilde {M}}(x,y)$
for any
![]() $x, y\in M$
with
$x, y\in M$
with
![]() $d(x,y)\leq \delta _A$
, we have that (UCℒ
) holds for
$d(x,y)\leq \delta _A$
, we have that (UCℒ
) holds for
![]() $R^{\tilde {M}}$
for all
$R^{\tilde {M}}$
for all
![]() $R\in \mathcal {L}$
. This shows that
$R\in \mathcal {L}$
. This shows that
is a continuous
![]() $\mathcal {L}$
-pre-structure.
$\mathcal {L}$
-pre-structure.
Note that the action
![]() $\pi : \Gamma \curvearrowright \tilde {\mathcal {M}}$
is still by automorphism, and that
$\pi : \Gamma \curvearrowright \tilde {\mathcal {M}}$
is still by automorphism, and that
![]() $\mathcal {A}$
is a substructure of
$\mathcal {A}$
is a substructure of
![]() $\tilde {\mathcal {M}}$
. Thus without loss of generality we may assume
$\tilde {\mathcal {M}}$
. Thus without loss of generality we may assume
![]() $\tilde {\mathcal {M}}=\mathcal {M}$
. In particular, we have that for all
$\tilde {\mathcal {M}}=\mathcal {M}$
. In particular, we have that for all
![]() $x, y\in M$
,
$x, y\in M$
,
![]() $d^M(x,y)\in P$
.
$d^M(x,y)\in P$
.
Also without loss of generality we may assume that for any
![]() $x\in M$
there is
$x\in M$
there is
![]() $a\in A$
and
$a\in A$
and
![]() $\gamma \in \Gamma $
with
$\gamma \in \Gamma $
with
![]() $x=\gamma \cdot a$
. In fact, let
$x=\gamma \cdot a$
. In fact, let
Then
![]() $M'$
is obviously a
$M'$
is obviously a
![]() $\pi $
-invariant subset, and hence
$\pi $
-invariant subset, and hence
![]() $\mathcal {M}'$
a
$\mathcal {M}'$
a
![]() $\pi $
-invariant substructure with
$\pi $
-invariant substructure with
![]() $A\subseteq M'$
. Thus without loss of generality we may assume
$A\subseteq M'$
. Thus without loss of generality we may assume
![]() $\mathcal {M}=\mathcal {M}'$
.
$\mathcal {M}=\mathcal {M}'$
.
Fix
![]() $a_1, \dots , a_m\in A$
such that
$a_1, \dots , a_m\in A$
such that
![]() $\{\Gamma a_i\,:\, 1\leq i\leq m\}$
form a partition of M, where
$\{\Gamma a_i\,:\, 1\leq i\leq m\}$
form a partition of M, where
Define
![]() $\rho :\Gamma \to {\mathrm {Part}}(\mathcal {A})$
by letting, for any
$\rho :\Gamma \to {\mathrm {Part}}(\mathcal {A})$
by letting, for any
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $a\in A$
,
$a\in A$
,
![]() $\rho (\gamma )(a)=\gamma \cdot a$
if
$\rho (\gamma )(a)=\gamma \cdot a$
if
![]() $\gamma \cdot a\in A$
, and
$\gamma \cdot a\in A$
, and
![]() $\rho (\gamma )(a)$
is undefined otherwise.
$\rho (\gamma )(a)$
is undefined otherwise.
Let
![]() $F\subseteq \Gamma $
be finite. Since
$F\subseteq \Gamma $
be finite. Since
![]() $\pi $
is faithful, by extending A and F with finitely many elements if necessary, we may assume without loss of generality that:
$\pi $
is faithful, by extending A and F with finitely many elements if necessary, we may assume without loss of generality that:
-
(i)
 $1_{\Gamma }\in F$
;
$1_{\Gamma }\in F$
; -
(ii)
 $F=F^{-1}$
;
$F=F^{-1}$
; -
(iii) for all
 $\gamma \in F$
such that
$\gamma \in F$
such that
 $\gamma \neq 1_{\Gamma }$
, there is
$\gamma \neq 1_{\Gamma }$
, there is
 $a\in A$
such that
$a\in A$
such that
 $a\neq \rho (\gamma )(a)\in A$
;
$a\neq \rho (\gamma )(a)\in A$
; -
(iv) for all
 $\gamma \in \Gamma $
there is some
$\gamma \in \Gamma $
there is some
 $\eta \in F$
such that
$\eta \in F$
such that
 $\rho (\gamma )=\rho (\eta )$
.
$\rho (\gamma )=\rho (\eta )$
.
For
![]() $1\leq i\leq m$
, define
$1\leq i\leq m$
, define
Since A and F are finite,
![]() $H_i$
is a finitely generated subgroup of
$H_i$
is a finitely generated subgroup of
![]() $\Gamma $
. Note that for any
$\Gamma $
. Note that for any
![]() $\gamma \in H_i$
, we have
$\gamma \in H_i$
, we have
![]() $\gamma \cdot a_i=a_i$
.
$\gamma \cdot a_i=a_i$
.
Let X be the disjoint union of left-coset spaces
Let
![]() $\Gamma $
act on X by left multiplication.
$\Gamma $
act on X by left multiplication.
We define a pseudometric
![]() $d^X$
on X as follows. For
$d^X$
on X as follows. For
![]() $\gamma , \eta \in \Gamma $
and
$\gamma , \eta \in \Gamma $
and
![]() $1\leq i, j\leq m$
,
$1\leq i, j\leq m$
,
Then it is easy to see that
![]() $d^X$
is well defined, and the
$d^X$
is well defined, and the
![]() $\Gamma $
action on X is by isometries.
$\Gamma $
action on X is by isometries.
Define
![]() $e: A\to X$
by
$e: A\to X$
by
 $$ \begin{align*}e(a)=\left\{\begin{array}{@{}ll} H_i, & \mbox{ if}\ a=a_i, \\ \gamma H_i, & \mbox{ if}\ a\neq a_i \mbox{ and}\ a=\gamma\cdot a_i\ \mbox{ for}\ \gamma\in F.\end{array}\right.\end{align*} $$
$$ \begin{align*}e(a)=\left\{\begin{array}{@{}ll} H_i, & \mbox{ if}\ a=a_i, \\ \gamma H_i, & \mbox{ if}\ a\neq a_i \mbox{ and}\ a=\gamma\cdot a_i\ \mbox{ for}\ \gamma\in F.\end{array}\right.\end{align*} $$
To see that e is well defined, first note that for any
![]() $a\in A\cap \Gamma a_i$
but
$a\in A\cap \Gamma a_i$
but
![]() $a\neq a_i$
, by (iv) there is
$a\neq a_i$
, by (iv) there is
![]() $\gamma \in F$
such that
$\gamma \in F$
such that
![]() $\gamma \cdot a_i=a$
, and thus
$\gamma \cdot a_i=a$
, and thus
![]() $e(a)$
is defined. Next, assume
$e(a)$
is defined. Next, assume
![]() $\gamma , \gamma '\in F$
such that
$\gamma , \gamma '\in F$
such that
![]() $\gamma \cdot a_i=\gamma '\cdot a_i\in A$
. Then
$\gamma \cdot a_i=\gamma '\cdot a_i\in A$
. Then
![]() $\gamma ^{-1}\in F$
and
$\gamma ^{-1}\in F$
and
![]() $\rho (\gamma ^{-1})(\rho (\gamma ')(a_i))=a_i$
, and hence
$\rho (\gamma ^{-1})(\rho (\gamma ')(a_i))=a_i$
, and hence
![]() $\gamma ^{-1}\gamma '\in H_i$
and
$\gamma ^{-1}\gamma '\in H_i$
and
![]() $\gamma H_i=\gamma 'H_i$
.
$\gamma H_i=\gamma 'H_i$
.
We claim that e is an isometric embedding from
![]() $(A, d^A)$
into
$(A, d^A)$
into
![]() $(X, d^X)$
. To see this, assume
$(X, d^X)$
. To see this, assume
![]() $a=\gamma \cdot a_i\in A$
and
$a=\gamma \cdot a_i\in A$
and
![]() $b=\eta \cdot a_j\in A$
for
$b=\eta \cdot a_j\in A$
for
![]() $\gamma , \eta \in F$
. Then
$\gamma , \eta \in F$
. Then
For any n-ary
![]() $R\in \mathcal {L}$
, define
$R\in \mathcal {L}$
, define
![]() $R^X$
on
$R^X$
on
by
We claim that for any n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $b_1, \dots , b_n\in A$
, letting
$b_1, \dots , b_n\in A$
, letting
![]() $\gamma _j\in F$
be such that
$\gamma _j\in F$
be such that
![]() $b_j=\gamma _j\cdot a_{i_j}$
for
$b_j=\gamma _j\cdot a_{i_j}$
for
![]() $1\leq j\leq n$
, we have
$1\leq j\leq n$
, we have
This is because
We claim that the following conditions hold:
-
(C1) For any
 $\gamma , \eta , \gamma ', \eta '\in F$
and
$\gamma , \eta , \gamma ', \eta '\in F$
and
 $1\leq i, j\leq m$
, if
$1\leq i, j\leq m$
, if
 $\gamma \cdot a_i, \gamma '\cdot a_{i}, \eta \cdot a_j, \eta '\cdot a_{j}\in A$
and then there does not exist
$\gamma \cdot a_i, \gamma '\cdot a_{i}, \eta \cdot a_j, \eta '\cdot a_{j}\in A$
and then there does not exist $$ \begin{align*}d^A(\gamma\cdot a_i, \eta\cdot a_j)\neq d^A(\gamma'\cdot a_{i}, \eta'\cdot a_{j}),\end{align*} $$
$$ \begin{align*}d^A(\gamma\cdot a_i, \eta\cdot a_j)\neq d^A(\gamma'\cdot a_{i}, \eta'\cdot a_{j}),\end{align*} $$
 $g\in \Gamma $
such that
$g\in \Gamma $
such that  $$ \begin{align*}g\gamma H_i=\gamma'H_i \mbox{ and } g\eta H_j=\eta' H_j.\end{align*} $$
$$ \begin{align*}g\gamma H_i=\gamma'H_i \mbox{ and } g\eta H_j=\eta' H_j.\end{align*} $$
-
(C2) For any
 $\gamma , \eta \in F$
and
$\gamma , \eta \in F$
and
 $1\leq i\leq m$
, if
$1\leq i\leq m$
, if
 $\gamma \cdot a_i, \eta \cdot a_i\in A$
and
$\gamma \cdot a_i, \eta \cdot a_i\in A$
and
 $\gamma \cdot a_i\neq \eta \cdot a_i$
, then
$\gamma \cdot a_i\neq \eta \cdot a_i$
, then
 $\gamma ^{-1}\eta \not \in H_i$
, i.e.,
$\gamma ^{-1}\eta \not \in H_i$
, i.e.,
 $\gamma H_i\neq \eta H_i$
.
$\gamma H_i\neq \eta H_i$
. -
(C3) For any
 $\gamma ,\eta , \gamma _1, \eta _1, \dots , \gamma _{\ell }, \eta _{\ell }\in F$
and
$\gamma ,\eta , \gamma _1, \eta _1, \dots , \gamma _{\ell }, \eta _{\ell }\in F$
and
 $1\leq i_0, \dots , i_{\ell }\leq m$
, if
$1\leq i_0, \dots , i_{\ell }\leq m$
, if
 $\gamma \cdot a_{i_0}, \eta \cdot a_{i_{\ell }}\in A$
and for all
$\gamma \cdot a_{i_0}, \eta \cdot a_{i_{\ell }}\in A$
and for all
 $1\leq j\leq \ell $
,
$1\leq j\leq \ell $
,
 $\gamma _j\cdot a_{i_{j-1}}, \eta _j\cdot a_{i_{j}}\in A$
, and then there do not exist
$\gamma _j\cdot a_{i_{j-1}}, \eta _j\cdot a_{i_{j}}\in A$
, and then there do not exist $$ \begin{align*}d^A(\gamma\cdot a_{i_0}, \eta\cdot a_{i_{\ell}})>\displaystyle\sum_{j=1}^{\ell} d^A(\gamma_j\cdot a_{i_{j-1}}, \eta_j\cdot a_{i_j}),\end{align*} $$
$$ \begin{align*}d^A(\gamma\cdot a_{i_0}, \eta\cdot a_{i_{\ell}})>\displaystyle\sum_{j=1}^{\ell} d^A(\gamma_j\cdot a_{i_{j-1}}, \eta_j\cdot a_{i_j}),\end{align*} $$
 $g_1,\dots , g_{\ell }\in \Gamma $
such that
$g_1,\dots , g_{\ell }\in \Gamma $
such that  $$ \begin{align*} \gamma H_{i_0}&=g_1 \gamma_1 H_{i_0} \\g_1 \eta_1 H_{i_1}&=g_2 \gamma_2 H_{i_1}, \\\cdots &\hspace{12pt} \cdots \\g_{\ell-1} \eta_{\ell-1} H_{i_{\ell-1}}& = g_{\ell} \gamma_{\ell} H_{i_{\ell-1}} \\g_{\ell} \eta_{\ell} H_{i_{\ell}}&= \eta H_{i_{\ell}}. \end{align*} $$
$$ \begin{align*} \gamma H_{i_0}&=g_1 \gamma_1 H_{i_0} \\g_1 \eta_1 H_{i_1}&=g_2 \gamma_2 H_{i_1}, \\\cdots &\hspace{12pt} \cdots \\g_{\ell-1} \eta_{\ell-1} H_{i_{\ell-1}}& = g_{\ell} \gamma_{\ell} H_{i_{\ell-1}} \\g_{\ell} \eta_{\ell} H_{i_{\ell}}&= \eta H_{i_{\ell}}. \end{align*} $$
-
(C4) For any n-ary
 $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
 $\gamma _1,\dots , \gamma _n, \eta _1,\dots , \eta _n\in F$
and
$\gamma _1,\dots , \gamma _n, \eta _1,\dots , \eta _n\in F$
and
 $1\leq i_1,\dots , i_n\leq m$
, if for all
$1\leq i_1,\dots , i_n\leq m$
, if for all
 $1\leq j\leq n$
,
$1\leq j\leq n$
,
 $\gamma _j\cdot a_{i_j}, \eta _j\cdot a_{i_j}\in A$
and there there does not exist
$\gamma _j\cdot a_{i_j}, \eta _j\cdot a_{i_j}\in A$
and there there does not exist $$ \begin{align*}R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})\neq R^A(\eta_1\cdot a_{i_1},\dots, \eta_n\cdot a_{i_n}),\end{align*} $$
$$ \begin{align*}R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})\neq R^A(\eta_1\cdot a_{i_1},\dots, \eta_n\cdot a_{i_n}),\end{align*} $$
 $g\in \Gamma $
such that
$g\in \Gamma $
such that  $$ \begin{align*} \gamma_1H_{i_1}&=g\eta_1H_{i_1} \\ \cdots &\hspace{12pt} \cdots \\ \gamma_n H_{i_n}& = g\eta_nH_{i_n}. \end{align*} $$
$$ \begin{align*} \gamma_1H_{i_1}&=g\eta_1H_{i_1} \\ \cdots &\hspace{12pt} \cdots \\ \gamma_n H_{i_n}& = g\eta_nH_{i_n}. \end{align*} $$
-
(C5) For any n-ary
 $R\in \mathcal {L}$
where
$R\in \mathcal {L}$
where
 $n\geq 2$
,
$n\geq 2$
,  $$ \begin{align*}E=\{\epsilon_1,\dots, \epsilon_t\}\subseteq\{1, \dots, n\},\end{align*} $$
$$ \begin{align*}E=\{\epsilon_1,\dots, \epsilon_t\}\subseteq\{1, \dots, n\},\end{align*} $$
 $$ \begin{align*}\gamma_1, \dots, \gamma_n, \eta_1,\dots, \eta_n\in F,\end{align*} $$
$$ \begin{align*}\gamma_1, \dots, \gamma_n, \eta_1,\dots, \eta_n\in F,\end{align*} $$
 $$ \begin{align*}\gamma_{1,1},\dots, \gamma_{1,\ell_1}, \eta_{1,1},\dots, \eta_{1,\ell_1}\in F,\end{align*} $$
$$ \begin{align*}\gamma_{1,1},\dots, \gamma_{1,\ell_1}, \eta_{1,1},\dots, \eta_{1,\ell_1}\in F,\end{align*} $$
 $$ \begin{align*}\cdots\cdots\end{align*} $$
$$ \begin{align*}\cdots\cdots\end{align*} $$
 $$ \begin{align*}\gamma_{t,1},\dots, \gamma_{t, \ell_t}, \eta_{t,1}, \dots, \eta_{t,\ell_t}\in F,\end{align*} $$
and
$$ \begin{align*}\gamma_{t,1},\dots, \gamma_{t, \ell_t}, \eta_{t,1}, \dots, \eta_{t,\ell_t}\in F,\end{align*} $$
and $$ \begin{align*}1\leq i_1, \dots, i_n, j_1,\dots, j_n \leq m,\end{align*} $$
if for all
$$ \begin{align*}1\leq i_1, \dots, i_n, j_1,\dots, j_n \leq m,\end{align*} $$
if for all $$ \begin{align*}1\leq i_{1,0}, i_{1,1}, \dots, i_{1,\ell_1}, \dots, i_{t,0}, i_{t,1},\dots, i_{t, \ell_t}\leq m,\end{align*} $$
$$ \begin{align*}1\leq i_{1,0}, i_{1,1}, \dots, i_{1,\ell_1}, \dots, i_{t,0}, i_{t,1},\dots, i_{t, \ell_t}\leq m,\end{align*} $$
 $1\leq k\leq n$
, for all
$1\leq k\leq n$
, for all $$ \begin{align*}\gamma_k\cdot a_{i_k}, \eta_k\cdot a_{j_k}\in A,\end{align*} $$
$$ \begin{align*}\gamma_k\cdot a_{i_k}, \eta_k\cdot a_{j_k}\in A,\end{align*} $$
 $1\leq s\leq t$
and
$1\leq s\leq t$
and
 $1\leq p\leq \ell _s$
,
$1\leq p\leq \ell _s$
,  $$ \begin{align*}i_{s,0}=i_{\epsilon_s}, i_{s, \ell_s}=j_{\epsilon_s},\end{align*} $$
for all
$$ \begin{align*}i_{s,0}=i_{\epsilon_s}, i_{s, \ell_s}=j_{\epsilon_s},\end{align*} $$
for all $$ \begin{align*}\gamma_s\cdot a_{i_{\epsilon_s}}, \eta_s\cdot a_{j_{\epsilon_s}}, \gamma_{s, p}\cdot a_{i_{s,p-1}}, \eta_{s, p}\cdot a_{i_{s,p}}\in A,\end{align*} $$
$$ \begin{align*}\gamma_s\cdot a_{i_{\epsilon_s}}, \eta_s\cdot a_{j_{\epsilon_s}}, \gamma_{s, p}\cdot a_{i_{s,p-1}}, \eta_{s, p}\cdot a_{i_{s,p}}\in A,\end{align*} $$
 $1\leq s\leq t$
, and
$1\leq s\leq t$
, and $$ \begin{align*}C_s=\displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s,p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s, p}})<\delta_A,\end{align*} $$
then there do not exist
$$ \begin{align*}C_s=\displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s,p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s, p}})<\delta_A,\end{align*} $$
then there do not exist $$ \begin{align*}\begin{array}{c}|R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_n\cdot a_{j_n})|> \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{c}|R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_n\cdot a_{j_n})|> \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A, \end{array} \end{align*} $$
 $g, h, g_{1,1}, \dots , g_{1,\ell _1}, \dots , g_{t,1}, \dots , g_{t, \ell _t}\in \Gamma $
such that for all
$g, h, g_{1,1}, \dots , g_{1,\ell _1}, \dots , g_{t,1}, \dots , g_{t, \ell _t}\in \Gamma $
such that for all
 $1\leq s\leq t$
,
$1\leq s\leq t$
,  $$ \begin{align*}g\gamma_{\epsilon_s}H_{i_{s,0}}&=g_{s,1}\gamma_{s,1}H_{i_{s,0}}, \\g_{s,1}\eta_{s,1}H_{i_{s,1}}&=g_{s,2}\gamma_{s,2}H_{i_{s,1}}, \\\dots &\hspace{12pt} \dots \\g_{s,\ell_s}\eta_{s, \ell_s}H_{i_{s, \ell_s}}&=h\eta_{\epsilon_s}H_{i_{s, \ell_s}}. \end{align*} $$
$$ \begin{align*}g\gamma_{\epsilon_s}H_{i_{s,0}}&=g_{s,1}\gamma_{s,1}H_{i_{s,0}}, \\g_{s,1}\eta_{s,1}H_{i_{s,1}}&=g_{s,2}\gamma_{s,2}H_{i_{s,1}}, \\\dots &\hspace{12pt} \dots \\g_{s,\ell_s}\eta_{s, \ell_s}H_{i_{s, \ell_s}}&=h\eta_{\epsilon_s}H_{i_{s, \ell_s}}. \end{align*} $$
The conditions (C1), (C2), and (C4) are easy to verify. For (C3), let
![]() $a=\gamma \cdot a_{i_0}$
,
$a=\gamma \cdot a_{i_0}$
,
![]() $b=\eta \cdot a_{i_{\ell }}$
and for all
$b=\eta \cdot a_{i_{\ell }}$
and for all
![]() $1\leq j\leq \ell $
, let
$1\leq j\leq \ell $
, let
![]() $b_j=\gamma _j\cdot a_{i_{j-1}}$
and
$b_j=\gamma _j\cdot a_{i_{j-1}}$
and
![]() $c_j=\eta _j\cdot a_{i_j}$
. Note that all these elements are in A. By our assumption, we have
$c_j=\eta _j\cdot a_{i_j}$
. Note that all these elements are in A. By our assumption, we have
 $$ \begin{align*}d^A(a, b)>\displaystyle\sum_{j=1}^{\ell} d^A(b_j, c_j).\end{align*} $$
$$ \begin{align*}d^A(a, b)>\displaystyle\sum_{j=1}^{\ell} d^A(b_j, c_j).\end{align*} $$
If there were
![]() $g_1, \dots , g_{\ell }\in \Gamma $
for which the left system of equations hold, then we have
$g_1, \dots , g_{\ell }\in \Gamma $
for which the left system of equations hold, then we have
![]() $e(a)=g_1\cdot e(b_1)$
,
$e(a)=g_1\cdot e(b_1)$
,
![]() $g_{\ell }\cdot e(c_{\ell })=e(b)$
, and for all
$g_{\ell }\cdot e(c_{\ell })=e(b)$
, and for all
![]() $1\leq j\leq \ell -1$
,
$1\leq j\leq \ell -1$
,
![]() $ g_j\cdot e(c_j)=g_{j+1}\cdot e(b_j)$
. Thus
$ g_j\cdot e(c_j)=g_{j+1}\cdot e(b_j)$
. Thus
 $$ \begin{align*}d^X(e(a), e(b)) &\leq \displaystyle\sum_{j=1}^{\ell-1} d^X(g_j\cdot e(b_j), g_j\cdot e(c_j)) \\&= \displaystyle\sum_{j=1}^{\ell-1} d^X(e(b_j), e(c_j)) \\&= \displaystyle\sum_{j=1}^{\ell-1} d^A(b_j, c_j)<d^A(a, b)=d^X(e(a), e(b)), \end{align*} $$
$$ \begin{align*}d^X(e(a), e(b)) &\leq \displaystyle\sum_{j=1}^{\ell-1} d^X(g_j\cdot e(b_j), g_j\cdot e(c_j)) \\&= \displaystyle\sum_{j=1}^{\ell-1} d^X(e(b_j), e(c_j)) \\&= \displaystyle\sum_{j=1}^{\ell-1} d^A(b_j, c_j)<d^A(a, b)=d^X(e(a), e(b)), \end{align*} $$
a contradiction.
For (C5), assume that all the hypotheses hold but there are
such that the displayed left system of equations hold. Then for all
![]() $1\leq s\leq t$
,
$1\leq s\leq t$
,
 $$ \begin{align*}g\gamma_{\epsilon_s}\cdot a_{i_{s,0}}&=g_{s,1}\gamma_{s, 1}\cdot a_{i_{s,0}},\\g_{s,1}\eta_{s,1}\cdot a_{i_{s,1}}& = g_{s,2}\gamma_{s,2}\cdot a_{i_{s,1}},\\\dots &\hspace{12pt} \dots \\g_{s,\ell_s}\eta_{s,\ell_s}\cdot a_{i_{s, \ell_s}}& = h\eta{\epsilon_s}\cdot a_{i_{s, \ell_s}}. \end{align*} $$
$$ \begin{align*}g\gamma_{\epsilon_s}\cdot a_{i_{s,0}}&=g_{s,1}\gamma_{s, 1}\cdot a_{i_{s,0}},\\g_{s,1}\eta_{s,1}\cdot a_{i_{s,1}}& = g_{s,2}\gamma_{s,2}\cdot a_{i_{s,1}},\\\dots &\hspace{12pt} \dots \\g_{s,\ell_s}\eta_{s,\ell_s}\cdot a_{i_{s, \ell_s}}& = h\eta{\epsilon_s}\cdot a_{i_{s, \ell_s}}. \end{align*} $$
Thus for
![]() $k=\epsilon _s\in E$
,
$k=\epsilon _s\in E$
,
 $$ \begin{align*}d^M(g\gamma_k\cdot a_{i_k}, h\eta_k\cdot a_{j_k})\leq \displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s, p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s,p}})=C_s<\delta_A.\end{align*} $$
$$ \begin{align*}d^M(g\gamma_k\cdot a_{i_k}, h\eta_k\cdot a_{j_k})\leq \displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s, p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s,p}})=C_s<\delta_A.\end{align*} $$
Since
![]() $\mathcal {M}$
is a continuous
$\mathcal {M}$
is a continuous
![]() $\mathcal {L}$
-pre-structure and the action of
$\mathcal {L}$
-pre-structure and the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathcal {M}$
is by automorphisms, we have
$\mathcal {M}$
is by automorphisms, we have
 $$ \begin{align*} & |R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_n\cdot a_{j_n})| \\& \quad = |R^M(g\gamma_1\cdot a_{i_1},\dots, g\gamma_n\cdot a_{i_n})-R^M(h\eta_1\cdot a_{j_1},\dots, h\eta_n\cdot a_{j_n})| \\& \quad \leq \displaystyle\sum_{k=1}^n K_{R,k}d^M(g\gamma_k\cdot a_{i_k}, h\eta_k\cdot a_{j_k}) \\& \quad \leq \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\sum_{k\not\in E} K_{R,k}\delta_A, \end{align*} $$
$$ \begin{align*} & |R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_n\cdot a_{j_n})| \\& \quad = |R^M(g\gamma_1\cdot a_{i_1},\dots, g\gamma_n\cdot a_{i_n})-R^M(h\eta_1\cdot a_{j_1},\dots, h\eta_n\cdot a_{j_n})| \\& \quad \leq \displaystyle\sum_{k=1}^n K_{R,k}d^M(g\gamma_k\cdot a_{i_k}, h\eta_k\cdot a_{j_k}) \\& \quad \leq \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\sum_{k\not\in E} K_{R,k}\delta_A, \end{align*} $$
a contradiction.
All of the conditions (C1)–(C5) are of the form which state that certain left systems of equations do not have solutions. Together, they amount to a finite number of such left systems. By the HL-property of
![]() $\Gamma $
, we obtain normal subgroups of finite index
$\Gamma $
, we obtain normal subgroups of finite index
![]() $K_1, \dots , K_m\unlhd \Gamma $
such that the same left systems of equations on
$K_1, \dots , K_m\unlhd \Gamma $
such that the same left systems of equations on
![]() $K_1H_1, \dots , K_mH_m$
still do not have solutions. By taking
$K_1H_1, \dots , K_mH_m$
still do not have solutions. By taking
![]() $K=\bigcap _{1\leq i\leq m} K_i$
we may assume without loss of generality that
$K=\bigcap _{1\leq i\leq m} K_i$
we may assume without loss of generality that
![]() $K_1=\cdots =K_m=K$
. This will simplify our notation and our discussions. The fact that the left systems on
$K_1=\cdots =K_m=K$
. This will simplify our notation and our discussions. The fact that the left systems on
![]() $KH_1,\dots , KH_m$
do not have solutions can in turn be expressed as the following conditions.
$KH_1,\dots , KH_m$
do not have solutions can in turn be expressed as the following conditions.
-
(K1) For any
 $\gamma , \eta , \gamma ', \eta '\in F$
and
$\gamma , \eta , \gamma ', \eta '\in F$
and
 $1\leq i, j\leq m$
, if
$1\leq i, j\leq m$
, if
 $\gamma \cdot a_i, \gamma '\cdot a_{i}, \eta \cdot a_j, \eta '\cdot a_{j}\in A$
and then there does not exist
$\gamma \cdot a_i, \gamma '\cdot a_{i}, \eta \cdot a_j, \eta '\cdot a_{j}\in A$
and then there does not exist $$ \begin{align*}d^A(\gamma\cdot a_i, \eta\cdot a_j)\neq d^A(\gamma'\cdot a_{i}, \eta'\cdot a_{j}),\end{align*} $$
$$ \begin{align*}d^A(\gamma\cdot a_i, \eta\cdot a_j)\neq d^A(\gamma'\cdot a_{i}, \eta'\cdot a_{j}),\end{align*} $$
 $g\in \Gamma $
such that
$g\in \Gamma $
such that  $$ \begin{align*}g\gamma KH_i=\gamma'KH_i \mbox{ and } g\eta KH_j=\eta' KH_j.\end{align*} $$
$$ \begin{align*}g\gamma KH_i=\gamma'KH_i \mbox{ and } g\eta KH_j=\eta' KH_j.\end{align*} $$
-
(K2) For any
 $\gamma , \eta \in F$
and
$\gamma , \eta \in F$
and
 $1\leq i\leq m$
, if
$1\leq i\leq m$
, if
 $\gamma \cdot a_i, \eta \cdot a_i\in A$
and
$\gamma \cdot a_i, \eta \cdot a_i\in A$
and
 $\gamma \cdot a_i\neq \eta \cdot a_i$
, then
$\gamma \cdot a_i\neq \eta \cdot a_i$
, then
 $\gamma ^{-1}\eta \not \in KH_i$
, i.e.,
$\gamma ^{-1}\eta \not \in KH_i$
, i.e.,
 $\gamma KH_i\neq \eta KH_i$
.
$\gamma KH_i\neq \eta KH_i$
. -
(K3) For any
 $\gamma ,\eta , \gamma _1, \eta _1, \dots , \gamma _{\ell }, \eta _{\ell }\in F$
and
$\gamma ,\eta , \gamma _1, \eta _1, \dots , \gamma _{\ell }, \eta _{\ell }\in F$
and
 $1\leq i_0, \dots , i_{\ell }\leq m$
, if
$1\leq i_0, \dots , i_{\ell }\leq m$
, if
 $\gamma \cdot a_{i_0}, \eta \cdot a_{i_{\ell }}\in A$
and for all
$\gamma \cdot a_{i_0}, \eta \cdot a_{i_{\ell }}\in A$
and for all
 $1\leq j\leq \ell $
,
$1\leq j\leq \ell $
,
 $\gamma _j\cdot a_{i_{j-1}}, \eta _j\cdot a_{i_{j}}\in A$
, and then there do not exist
$\gamma _j\cdot a_{i_{j-1}}, \eta _j\cdot a_{i_{j}}\in A$
, and then there do not exist $$ \begin{align*}d^A(\gamma\cdot a_{i_0}, \eta\cdot a_{i_{\ell}})>\displaystyle\sum_{j=1}^{\ell} d^A(\gamma_j\cdot a_{i_{j-1}}, \eta_j\cdot a_{i_j}),\end{align*} $$
$$ \begin{align*}d^A(\gamma\cdot a_{i_0}, \eta\cdot a_{i_{\ell}})>\displaystyle\sum_{j=1}^{\ell} d^A(\gamma_j\cdot a_{i_{j-1}}, \eta_j\cdot a_{i_j}),\end{align*} $$
 $g_1,\dots , g_{\ell }\in \Gamma $
such that:
$g_1,\dots , g_{\ell }\in \Gamma $
such that:  $$ \begin{align*}\gamma KH_{i_0}&=g_1 \gamma_1 KH_{i_0}, \\g_1 \eta_1 KH_{i_1}&=g_2 \gamma_2 KH_{i_1}, \\\cdots &\hspace{12pt} \cdots \\g_{\ell-1} \eta_{\ell-1} KH_{i_{\ell-1}}& = g_{\ell} \gamma_{\ell} KH_{i_{\ell-1}}, \\g_{\ell} \eta_{\ell} KH_{i_{\ell}}&= \eta KH_{i_{\ell}}. \end{align*} $$
$$ \begin{align*}\gamma KH_{i_0}&=g_1 \gamma_1 KH_{i_0}, \\g_1 \eta_1 KH_{i_1}&=g_2 \gamma_2 KH_{i_1}, \\\cdots &\hspace{12pt} \cdots \\g_{\ell-1} \eta_{\ell-1} KH_{i_{\ell-1}}& = g_{\ell} \gamma_{\ell} KH_{i_{\ell-1}}, \\g_{\ell} \eta_{\ell} KH_{i_{\ell}}&= \eta KH_{i_{\ell}}. \end{align*} $$
-
(K4) For any n-ary
 $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
 $\gamma _1,\dots , \gamma _n, \eta _1,\dots , \eta _n\in F$
and
$\gamma _1,\dots , \gamma _n, \eta _1,\dots , \eta _n\in F$
and
 $1\leq i_1,\dots , i_n\leq m$
, if for all
$1\leq i_1,\dots , i_n\leq m$
, if for all
 $1\leq j\leq n$
,
$1\leq j\leq n$
,
 $\gamma _j\cdot a_{i_j}, \eta _j\cdot a_{i_j}\in A$
and then there does not exist
$\gamma _j\cdot a_{i_j}, \eta _j\cdot a_{i_j}\in A$
and then there does not exist $$ \begin{align*}R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})\neq R^A(\eta_1\cdot a_{i_1},\dots, \eta_n\cdot a_{i_n}),\end{align*} $$
$$ \begin{align*}R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})\neq R^A(\eta_1\cdot a_{i_1},\dots, \eta_n\cdot a_{i_n}),\end{align*} $$
 $g\in \Gamma $
such that:
$g\in \Gamma $
such that:  $$ \begin{align*}\gamma_1KH_{i_1}&=g\eta_1KH_{i_1}, \\ \cdots &\hspace{12pt} \cdots \\ \gamma_n KH_{i_n}& = g\eta_nKH_{i_n}. \end{align*} $$
$$ \begin{align*}\gamma_1KH_{i_1}&=g\eta_1KH_{i_1}, \\ \cdots &\hspace{12pt} \cdots \\ \gamma_n KH_{i_n}& = g\eta_nKH_{i_n}. \end{align*} $$
-
(K5) For any n-ary
 $R\in \mathcal {L}$
where
$R\in \mathcal {L}$
where
 $n\geq 2$
,
$n\geq 2$
,  $$ \begin{align*}E=\{\epsilon_1,\dots, \epsilon_t\}\subseteq\{1, \dots, n\},\end{align*} $$
$$ \begin{align*}E=\{\epsilon_1,\dots, \epsilon_t\}\subseteq\{1, \dots, n\},\end{align*} $$
 $$ \begin{align*}\gamma_1, \dots, \gamma_n, \eta_1,\dots, \eta_n\in F,\end{align*} $$
$$ \begin{align*}\gamma_1, \dots, \gamma_n, \eta_1,\dots, \eta_n\in F,\end{align*} $$
 $$ \begin{align*}\gamma_{1,1},\dots, \gamma_{1,\ell_1}, \eta_{1,1},\dots, \eta_{1,\ell_1}\in F,\end{align*} $$
$$ \begin{align*}\gamma_{1,1},\dots, \gamma_{1,\ell_1}, \eta_{1,1},\dots, \eta_{1,\ell_1}\in F,\end{align*} $$
 $$ \begin{align*}\cdots\cdots\end{align*} $$
$$ \begin{align*}\cdots\cdots\end{align*} $$
 $$ \begin{align*}\gamma_{t,1},\dots, \gamma_{t, \ell_t}, \eta_{t,1}, \dots, \eta_{t,\ell_t}\in F,\end{align*} $$
and
$$ \begin{align*}\gamma_{t,1},\dots, \gamma_{t, \ell_t}, \eta_{t,1}, \dots, \eta_{t,\ell_t}\in F,\end{align*} $$
and $$ \begin{align*}1\leq i_1, \dots, i_n, j_1,\dots, j_n \leq m,\end{align*} $$
if for all
$$ \begin{align*}1\leq i_1, \dots, i_n, j_1,\dots, j_n \leq m,\end{align*} $$
if for all $$ \begin{align*}1\leq i_{1,0}, i_{1,1}, \dots, i_{1,\ell_1}, \dots, i_{t,0}, i_{t,1},\dots, i_{t, \ell_t}\leq m,\end{align*} $$
$$ \begin{align*}1\leq i_{1,0}, i_{1,1}, \dots, i_{1,\ell_1}, \dots, i_{t,0}, i_{t,1},\dots, i_{t, \ell_t}\leq m,\end{align*} $$
 $1\leq k\leq n$
, for all
$1\leq k\leq n$
, for all $$ \begin{align*}\gamma_k\cdot a_{i_k}, \eta_k\cdot a_{j_k}\in A,\end{align*} $$
$$ \begin{align*}\gamma_k\cdot a_{i_k}, \eta_k\cdot a_{j_k}\in A,\end{align*} $$
 $1\leq s\leq t$
and
$1\leq s\leq t$
and
 $1\leq p\leq \ell _s$
,
$1\leq p\leq \ell _s$
,  $$ \begin{align*}i_{s,0}=i_{\epsilon_s}, i_{s, \ell_s}=j_{\epsilon_s},\end{align*} $$
for all
$$ \begin{align*}i_{s,0}=i_{\epsilon_s}, i_{s, \ell_s}=j_{\epsilon_s},\end{align*} $$
for all $$ \begin{align*}\gamma_s\cdot a_{i_{\epsilon_s}}, \eta_s\cdot a_{j_{\epsilon_s}}, \gamma_{s, p}\cdot a_{i_{s,p-1}}, \eta_{s, p}\cdot a_{i_{s,p}}\in A,\end{align*} $$
$$ \begin{align*}\gamma_s\cdot a_{i_{\epsilon_s}}, \eta_s\cdot a_{j_{\epsilon_s}}, \gamma_{s, p}\cdot a_{i_{s,p-1}}, \eta_{s, p}\cdot a_{i_{s,p}}\in A,\end{align*} $$
 $1\leq s\leq t$
, and
$1\leq s\leq t$
, and $$ \begin{align*}C_s=\displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s,p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s, p}})<\delta_A,\end{align*} $$
then there do not exist
$$ \begin{align*}C_s=\displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s,p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s, p}})<\delta_A,\end{align*} $$
then there do not exist $$ \begin{align*}\begin{array}{c}|R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_n\cdot a_{j_n})|>\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{c}|R^A(\gamma_1\cdot a_{i_1},\dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_n\cdot a_{j_n})|>\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A, \end{array} \end{align*} $$
 $g, h, g_{1,1}, \dots , g_{1,\ell _1}, \dots , g_{t,1}, \dots , g_{t, \ell _t}\in \Gamma $
such that for all
$g, h, g_{1,1}, \dots , g_{1,\ell _1}, \dots , g_{t,1}, \dots , g_{t, \ell _t}\in \Gamma $
such that for all
 $1\leq s\leq t$
,
$1\leq s\leq t$
,  $$ \begin{align*} g\gamma_{\epsilon_s}KH_{i_{s,0}}&=g_{s,1}\gamma_{s,1}KH_{i_{s,0}}, \\ g_{s,1}\eta_{s,1}KH_{i_{s,1}}&=g_{s,2}\gamma_{s,2}KH_{i_{s,1}}, \\ \dots &\hspace{12pt} \dots \\ g_{s,\ell_s}\eta_{s, \ell_s}KH_{i_{s, \ell_s}}&=h\eta_{\epsilon_s}KH_{i_{s, \ell_s}}. \end{align*} $$
$$ \begin{align*} g\gamma_{\epsilon_s}KH_{i_{s,0}}&=g_{s,1}\gamma_{s,1}KH_{i_{s,0}}, \\ g_{s,1}\eta_{s,1}KH_{i_{s,1}}&=g_{s,2}\gamma_{s,2}KH_{i_{s,1}}, \\ \dots &\hspace{12pt} \dots \\ g_{s,\ell_s}\eta_{s, \ell_s}KH_{i_{s, \ell_s}}&=h\eta_{\epsilon_s}KH_{i_{s, \ell_s}}. \end{align*} $$
Let Y be the disjoint union of the left-coset spaces
Let
![]() $\Gamma $
act on Y by left multiplication.
$\Gamma $
act on Y by left multiplication.
We define a metric
![]() $d^Y$
on Y as follows. For
$d^Y$
on Y as follows. For
![]() $\gamma , \eta \in \Gamma $
and
$\gamma , \eta \in \Gamma $
and
![]() $1\leq i, j\leq m$
,
$1\leq i, j\leq m$
,
where
![]() $(p_1, \dots , p_\ell )\in S_{\gamma , \eta , i, j}$
if there are
$(p_1, \dots , p_\ell )\in S_{\gamma , \eta , i, j}$
if there are
and
such that
for all
![]() $1\leq k\leq \ell $
,
$1\leq k\leq \ell $
,
and
 $$ \begin{align*}\gamma KH_{i_0}&=g_1 \gamma_1 KH_{i_0}, \\ g_1 \eta_1 KH_{i_1}&=g_2 \gamma_2 KH_{i_1}, \\ \cdots &\hspace{12pt} \cdots \\ g_{\ell-1} \eta_{\ell-1} KH_{i_{\ell-1}}& = g_{\ell} \gamma_{\ell} KH_{i_{\ell-1}}, \\ g_{\ell} \eta_{\ell} KH_{i_{\ell}}&= \eta KH_{i_{\ell}}. \end{align*} $$
$$ \begin{align*}\gamma KH_{i_0}&=g_1 \gamma_1 KH_{i_0}, \\ g_1 \eta_1 KH_{i_1}&=g_2 \gamma_2 KH_{i_1}, \\ \cdots &\hspace{12pt} \cdots \\ g_{\ell-1} \eta_{\ell-1} KH_{i_{\ell-1}}& = g_{\ell} \gamma_{\ell} KH_{i_{\ell-1}}, \\ g_{\ell} \eta_{\ell} KH_{i_{\ell}}&= \eta KH_{i_{\ell}}. \end{align*} $$
It is clear that
![]() $d^Y$
is invariant under the action of
$d^Y$
is invariant under the action of
![]() $\Gamma $
.
$\Gamma $
.
Lemma 7.9.
![]() $d^Y$
is a metric on Y.
$d^Y$
is a metric on Y.
Proof We first verify that if
![]() $i\neq j$
or (
$i\neq j$
or (
![]() $i=j$
but
$i=j$
but
![]() $\gamma ^{-1}\eta \not \in KH_i$
) then
$\gamma ^{-1}\eta \not \in KH_i$
) then
If
![]() $S_{\gamma , \eta , i, j}=\varnothing $
then
$S_{\gamma , \eta , i, j}=\varnothing $
then
![]() $d^Y(\gamma KH_i, \eta KH_j)=\delta _A>0$
. So suppose
$d^Y(\gamma KH_i, \eta KH_j)=\delta _A>0$
. So suppose
![]() $S_{\gamma , \eta , i, j}\neq \varnothing $
. Note that, however, since F and A are finite, the number of elements
$S_{\gamma , \eta , i, j}\neq \varnothing $
. Note that, however, since F and A are finite, the number of elements
![]() $(p_1, \dots , p_{\ell })\in S_{\gamma , \eta , i, j}$
such that
$(p_1, \dots , p_{\ell })\in S_{\gamma , \eta , i, j}$
such that
![]() $p_1, \dots , p_\ell \neq 0$
and
$p_1, \dots , p_\ell \neq 0$
and
![]() $p_1+\cdots +p_{\ell }\leq \delta _A$
is finite. Now suppose
$p_1+\cdots +p_{\ell }\leq \delta _A$
is finite. Now suppose
![]() $i\neq j$
. Then since
$i\neq j$
. Then since
![]() $\Gamma a_i\cap \Gamma a_j=\varnothing $
, for any
$\Gamma a_i\cap \Gamma a_j=\varnothing $
, for any
![]() $(p_1, \dots , p_\ell )\in S_{\gamma , \eta , i, j}$
,
$(p_1, \dots , p_\ell )\in S_{\gamma , \eta , i, j}$
,
![]() $p_1+\cdots +p_{\ell }>0$
because some term is positive. Thus
$p_1+\cdots +p_{\ell }>0$
because some term is positive. Thus
![]() $d^Y(\gamma KH_i, \eta KH_j)>0$
. Next suppose
$d^Y(\gamma KH_i, \eta KH_j)>0$
. Next suppose
![]() $i=j$
but
$i=j$
but
![]() $\gamma ^{-1}\eta \not \in KH_i$
. In this case if some
$\gamma ^{-1}\eta \not \in KH_i$
. In this case if some
![]() $i_k\neq i$
for
$i_k\neq i$
for
![]() $1\leq k\leq \ell $
, then by the same argument
$1\leq k\leq \ell $
, then by the same argument
![]() $p_1+\dots +p_\ell>0$
. Otherwise,
$p_1+\dots +p_\ell>0$
. Otherwise,
![]() $i_k=i$
for all
$i_k=i$
for all
![]() $1\leq k\leq \ell $
. In this case
$1\leq k\leq \ell $
. In this case
 $$ \begin{align*}p_1+\cdots+p_{\ell}=\displaystyle\sum_{j=1}^{\ell}d^A(\gamma_j\cdot a_i, \eta_j\cdot a_i).\end{align*} $$
$$ \begin{align*}p_1+\cdots+p_{\ell}=\displaystyle\sum_{j=1}^{\ell}d^A(\gamma_j\cdot a_i, \eta_j\cdot a_i).\end{align*} $$
Again, if some of them are positive, then we are done. If all of them are zero, then
![]() $\gamma _j^{-1}\eta _j\in H_i$
for all
$\gamma _j^{-1}\eta _j\in H_i$
for all
![]() $1\leq j\leq \ell $
. In particular
$1\leq j\leq \ell $
. In particular
![]() $\gamma _j KH_i=\eta _j KH_i$
for all
$\gamma _j KH_i=\eta _j KH_i$
for all
![]() $1\leq j\leq \ell $
. By the defining relation for
$1\leq j\leq \ell $
. By the defining relation for
![]() $(p_1,\dots , p_\ell )\in S_{\gamma ,\eta , i, j}$
we get
$(p_1,\dots , p_\ell )\in S_{\gamma ,\eta , i, j}$
we get
 $$ \begin{align*}\gamma KH_{i}&=g_1 \gamma_1 KH_{i}, \\ g_1 \eta_1 KH_{i}&=g_2 \gamma_2 KH_{i}, \\ \cdots &\hspace{12pt} \cdots \\ g_{\ell-1} \eta_{\ell-1} KH_{i}& = g_{\ell} \gamma_{\ell} KH_{i}, \\ g_{\ell} \eta_{\ell} KH_{i}&= \eta KH_{i}. \end{align*} $$
$$ \begin{align*}\gamma KH_{i}&=g_1 \gamma_1 KH_{i}, \\ g_1 \eta_1 KH_{i}&=g_2 \gamma_2 KH_{i}, \\ \cdots &\hspace{12pt} \cdots \\ g_{\ell-1} \eta_{\ell-1} KH_{i}& = g_{\ell} \gamma_{\ell} KH_{i}, \\ g_{\ell} \eta_{\ell} KH_{i}&= \eta KH_{i}. \end{align*} $$
But now all the terms of these equations are equal. So we get
![]() $\gamma KH_i=\eta KH_i$
.
$\gamma KH_i=\eta KH_i$
.
Next we verify the triangle inequality. Suppose
and
for
![]() $(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i, j}$
and
$(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i, j}$
and
![]() $(q_1, \dots , q_t)\in S_{\eta , \mu , j, k}$
. Concatenating the defining relations for
$(q_1, \dots , q_t)\in S_{\eta , \mu , j, k}$
. Concatenating the defining relations for
![]() $(p_1,\dots , p_\ell )$
and
$(p_1,\dots , p_\ell )$
and
![]() $(q_1,\dots , q_t)$
, we obtain a left system for
$(q_1,\dots , q_t)$
, we obtain a left system for
![]() $(p_1,\dots , p_{\ell }, q_1,\dots , q_t)\in S_{\gamma , \mu , i, k}$
. Thus
$(p_1,\dots , p_{\ell }, q_1,\dots , q_t)\in S_{\gamma , \mu , i, k}$
. Thus
Lemma 7.10. For any
![]() $\gamma , \eta \in F$
and
$\gamma , \eta \in F$
and
![]() $1\leq i,j\leq m$
, if
$1\leq i,j\leq m$
, if
![]() $\gamma \cdot a_i, \eta \cdot a_j\in A$
, then
$\gamma \cdot a_i, \eta \cdot a_j\in A$
, then
Proof Suppose
where
![]() $(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i, j}$
is witnessed by
$(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i, j}$
is witnessed by
![]() $g_1,\dots , g_\ell \in \Gamma $
,
$g_1,\dots , g_\ell \in \Gamma $
,
![]() $\gamma _1,\eta _1,\dots , \gamma _\ell , \eta _\ell \in F$
and
$\gamma _1,\eta _1,\dots , \gamma _\ell , \eta _\ell \in F$
and
![]() $1\leq i_0, \dots , i_\ell \leq m$
. Then by the defining left system of equations for
$1\leq i_0, \dots , i_\ell \leq m$
. Then by the defining left system of equations for
![]() $(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i,j}$
and (K3), we have
$(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i,j}$
and (K3), we have
Conversely, from the trivial system of equations
we get that
Next we define
![]() $R^Y$
for an n-ary
$R^Y$
for an n-ary
![]() $R\in \mathcal {L}$
on
$R\in \mathcal {L}$
on
by
By (K4), this is well defined. It is clear that
![]() ${\mathrm {dom}}(R^Y)$
and
${\mathrm {dom}}(R^Y)$
and
![]() $R^Y$
are invariant under the action of
$R^Y$
are invariant under the action of
![]() $\Gamma $
.
$\Gamma $
.
Lemma 7.11.
![]() $\mathcal {Y}=(Y, d^Y, (R^Y)_{R\in \mathcal {L}})$
is a partially defined continuous
$\mathcal {Y}=(Y, d^Y, (R^Y)_{R\in \mathcal {L}})$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure.
$\mathcal {L}$
-pre-structure.
Proof Suppose first R is unary. We verify (UCℒ
) for R. Let
![]() $\gamma , \eta \in \Gamma $
and
$\gamma , \eta \in \Gamma $
and
![]() $1\leq i, j\leq m$
. Assume
$1\leq i, j\leq m$
. Assume
where
![]() $(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i, j}$
is witnessed by
$(p_1,\dots , p_\ell )\in S_{\gamma , \eta , i, j}$
is witnessed by
![]() $g_1, \dots , g_\ell \in \Gamma $
,
$g_1, \dots , g_\ell \in \Gamma $
,
![]() $\gamma _1,\eta _1,\dots , \gamma _\ell , \eta _\ell \in F$
, and
$\gamma _1,\eta _1,\dots , \gamma _\ell , \eta _\ell \in F$
, and
![]() $1\leq i_0, \dots , i_{\ell }\leq m$
. For
$1\leq i_0, \dots , i_{\ell }\leq m$
. For
![]() $1\leq k\leq \ell $
, let
$1\leq k\leq \ell $
, let
![]() $b_k=\gamma _k\cdot a_{i_{k-1}}\in A$
and
$b_k=\gamma _k\cdot a_{i_{k-1}}\in A$
and
![]() $c_k=\eta _k\cdot a_{i_k}\in A$
. Then
$c_k=\eta _k\cdot a_{i_k}\in A$
. Then
and
 $$ \begin{align*}d^Y(\gamma KH_i, \eta KH_j)= p_1+\cdots+p_\ell =\displaystyle\sum_{k=1}^{\ell} d^A(b_k, c_k).\end{align*} $$
$$ \begin{align*}d^Y(\gamma KH_i, \eta KH_j)= p_1+\cdots+p_\ell =\displaystyle\sum_{k=1}^{\ell} d^A(b_k, c_k).\end{align*} $$
We may assume
![]() $d^Y(\gamma KH_i, \eta KH_j)\in I_{R,1}$
; otherwise the desired inequality trivially holds. Now by the defining equations of
$d^Y(\gamma KH_i, \eta KH_j)\in I_{R,1}$
; otherwise the desired inequality trivially holds. Now by the defining equations of
![]() $S_{\gamma , \eta , i, j}$
, we have
$S_{\gamma , \eta , i, j}$
, we have
 $$ \begin{align*}|R^Y(\gamma KH_i)-R^Y(\eta KH_j)| &\leq \displaystyle\sum_{k=1}^{\ell} |R^Y(\gamma_kKH_{i_{k-1}})-R^Y(\eta_kKH_{i_k})| \\&= \displaystyle\sum_{k=1}^{\ell} |R^A(b_k)-R^A(c_k)| \\&\leq \displaystyle\sum_{k=1}^{\ell} \mathfrak{u}_{R,1}(d^A(b_k, c_k)) \\&\leq \mathfrak{u}_{R,1}(d^Y(\gamma KH_i, \eta KH_j)). \end{align*} $$
$$ \begin{align*}|R^Y(\gamma KH_i)-R^Y(\eta KH_j)| &\leq \displaystyle\sum_{k=1}^{\ell} |R^Y(\gamma_kKH_{i_{k-1}})-R^Y(\eta_kKH_{i_k})| \\&= \displaystyle\sum_{k=1}^{\ell} |R^A(b_k)-R^A(c_k)| \\&\leq \displaystyle\sum_{k=1}^{\ell} \mathfrak{u}_{R,1}(d^A(b_k, c_k)) \\&\leq \mathfrak{u}_{R,1}(d^Y(\gamma KH_i, \eta KH_j)). \end{align*} $$
Now it follows that
Next suppose R is n-ary for
![]() $n\geq 2$
. Let
$n\geq 2$
. Let
![]() $\gamma , \eta \in \Gamma $
,
$\gamma , \eta \in \Gamma $
,
![]() $\gamma _1, \dots , \gamma _n, \eta _1, \dots , \eta _n\in F$
and
$\gamma _1, \dots , \gamma _n, \eta _1, \dots , \eta _n\in F$
and
![]() $1\leq i_1,\dots , i_n, j_1, \dots , j_n\leq m$
. Suppose
$1\leq i_1,\dots , i_n, j_1, \dots , j_n\leq m$
. Suppose
![]() $\gamma _k\cdot a_{i_k}, \eta _k\cdot a_{j_k}\in A$
for all
$\gamma _k\cdot a_{i_k}, \eta _k\cdot a_{j_k}\in A$
for all
![]() $1\leq k\leq n$
. We need to show that
$1\leq k\leq n$
. We need to show that
 $$ \begin{align*}\begin{array}{c} |R^Y(\gamma\gamma_1KH_{i_1}, \dots, \gamma\gamma_nKH_{i_n})-R^Y(\eta\eta_1KH_{j_1},\dots, \eta\eta_nKH_{j_n})| \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \leq\ \displaystyle\sum_{k=1}^n K_{R,k}d^Y(\gamma\gamma_kKH_{i_k}, \eta\eta_kKH_{j_k}). \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{c} |R^Y(\gamma\gamma_1KH_{i_1}, \dots, \gamma\gamma_nKH_{i_n})-R^Y(\eta\eta_1KH_{j_1},\dots, \eta\eta_nKH_{j_n})| \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \leq\ \displaystyle\sum_{k=1}^n K_{R,k}d^Y(\gamma\gamma_kKH_{i_k}, \eta\eta_kKH_{j_k}). \end{array}\end{align*} $$
Let E be the set of
![]() $k\in \{1, \dots , n\}$
such that
$k\in \{1, \dots , n\}$
such that
Enumerate the elements of E as
![]() $\epsilon _1,\dots , \epsilon _t$
. Then for each
$\epsilon _1,\dots , \epsilon _t$
. Then for each
![]() $1\leq s\leq t$
, by the definition of
$1\leq s\leq t$
, by the definition of
![]() $d^Y$
, there are
$d^Y$
, there are
and
such that
for all
![]() $1\leq p\leq \ell _s$
,
$1\leq p\leq \ell _s$
,
 $$ \begin{align*}d^Y(\gamma\gamma_{\epsilon_s}KH_{i_{\epsilon_s}},\eta\eta_{\epsilon_s}KH_{j_{\epsilon_s}}) =\displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s,p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s,p}})=C_s,\end{align*} $$
$$ \begin{align*}d^Y(\gamma\gamma_{\epsilon_s}KH_{i_{\epsilon_s}},\eta\eta_{\epsilon_s}KH_{j_{\epsilon_s}}) =\displaystyle\sum_{p=1}^{\ell_s} d^A(\gamma_{s,p}\cdot a_{i_{s,p-1}}, \eta_{s,p}\cdot a_{i_{s,p}})=C_s,\end{align*} $$
and
 $$ \begin{align*}\gamma\gamma_{\epsilon_s}KH_{i_{s,0}}&=g_{s,1}\gamma_{s,1}KH_{i_{s,0}}, \\ g_{s,1}\eta_{s,1}KH_{i_{s,1}}&=g_{s,2}\gamma_{s,2}KH_{i_{s,1}}, \\ \dots &\hspace{12pt} \dots \\ g_{s,\ell_s}\eta_{s, \ell_s}KH_{i_{s, \ell_s}}&=\eta\eta_{\epsilon_s}KH_{i_{s, \ell_s}}. \end{align*} $$
$$ \begin{align*}\gamma\gamma_{\epsilon_s}KH_{i_{s,0}}&=g_{s,1}\gamma_{s,1}KH_{i_{s,0}}, \\ g_{s,1}\eta_{s,1}KH_{i_{s,1}}&=g_{s,2}\gamma_{s,2}KH_{i_{s,1}}, \\ \dots &\hspace{12pt} \dots \\ g_{s,\ell_s}\eta_{s, \ell_s}KH_{i_{s, \ell_s}}&=\eta\eta_{\epsilon_s}KH_{i_{s, \ell_s}}. \end{align*} $$
For
![]() $k\not \in E$
,
$k\not \in E$
,
Thus
 $$ \begin{align*}\displaystyle\sum_{k=1}^n K_{R,k}d^Y(\gamma\gamma_kKH_{i_k}, \eta\eta_kKH_{j_k})= \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A. \end{align*} $$
$$ \begin{align*}\displaystyle\sum_{k=1}^n K_{R,k}d^Y(\gamma\gamma_kKH_{i_k}, \eta\eta_kKH_{j_k})= \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A. \end{align*} $$
By (K5) we have
 $$ \begin{align*} &|R^A(\gamma_1\cdot a_{i_1}, \dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_1\cdot a_{j_n})| \\& \quad \leq \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A \\& \quad = \displaystyle\sum_{k=1}^n K_{R,k}d^Y(\gamma\gamma_kKH_{i_k}, \eta\eta_kKH_{j_k}). \end{align*} $$
$$ \begin{align*} &|R^A(\gamma_1\cdot a_{i_1}, \dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_1\cdot a_{j_n})| \\& \quad \leq \displaystyle\sum_{k=\epsilon_s\in E} K_{R,k}C_s+\displaystyle\sum_{k\not\in E} K_{R,k}\delta_A \\& \quad = \displaystyle\sum_{k=1}^n K_{R,k}d^Y(\gamma\gamma_kKH_{i_k}, \eta\eta_kKH_{j_k}). \end{align*} $$
However, note that
 $$ \begin{align*}& |R^Y(\gamma\gamma_1KH_{i_1}, \dots, \gamma\gamma_nKH_{i_n})-R^Y(\eta\eta_1KH_{j_1},\dots, \eta\eta_nKH_{j_n})| \\&\quad = |R^Y(\gamma_1KH_{i_1}, \dots, \gamma_nKH_{i_n})-R^Y(\eta_1KH_{j_1},\dots, \eta_nKH_{j_n})| \\&\quad = |R^A(\gamma_1\cdot a_{i_1}, \dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_1\cdot a_{j_n})|. \end{align*} $$
$$ \begin{align*}& |R^Y(\gamma\gamma_1KH_{i_1}, \dots, \gamma\gamma_nKH_{i_n})-R^Y(\eta\eta_1KH_{j_1},\dots, \eta\eta_nKH_{j_n})| \\&\quad = |R^Y(\gamma_1KH_{i_1}, \dots, \gamma_nKH_{i_n})-R^Y(\eta_1KH_{j_1},\dots, \eta_nKH_{j_n})| \\&\quad = |R^A(\gamma_1\cdot a_{i_1}, \dots, \gamma_n\cdot a_{i_n})-R^A(\eta_1\cdot a_{j_1},\dots, \eta_1\cdot a_{j_n})|. \end{align*} $$
We thus obtained the desired inequality.
Let
![]() $\mathcal {N}$
be the conservative extension of
$\mathcal {N}$
be the conservative extension of
![]() $\mathcal {Y}$
given by Lemma 3.7. In particular, for every n-ary
$\mathcal {Y}$
given by Lemma 3.7. In particular, for every n-ary
![]() $R\in \mathcal {L}$
and
$R\in \mathcal {L}$
and
![]() $\overline {x}\in N^n$
,
$\overline {x}\in N^n$
,
It is clear that
![]() $R^N$
is invariant under the action of
$R^N$
is invariant under the action of
![]() $\Gamma $
.
$\Gamma $
.
Define
![]() $f: A \to N$
by
$f: A \to N$
by
 $$ \begin{align*}f(a)=\left\{\begin{array}{@{}ll} KH_i, & \mbox{ if}\ a=a_i, \\ \gamma KH_i, & \mbox{ if}\ a\neq a_i\ \mbox{ and}\ a=\gamma\cdot a_i\ \mbox{ for}\ \gamma\in F. \end{array}\right. \end{align*} $$
$$ \begin{align*}f(a)=\left\{\begin{array}{@{}ll} KH_i, & \mbox{ if}\ a=a_i, \\ \gamma KH_i, & \mbox{ if}\ a\neq a_i\ \mbox{ and}\ a=\gamma\cdot a_i\ \mbox{ for}\ \gamma\in F. \end{array}\right. \end{align*} $$
It is easy to see that f is well defined. We claim that f is an isomorphic embedding from
![]() $\mathcal {A}$
into
$\mathcal {A}$
into
![]() $\mathcal {N}$
. For injectivity, let
$\mathcal {N}$
. For injectivity, let
![]() $\gamma , \eta \in F$
such that
$\gamma , \eta \in F$
such that
![]() $\gamma \cdot a_i, \eta \cdot a_i\in A$
but
$\gamma \cdot a_i, \eta \cdot a_i\in A$
but
![]() $\gamma \cdot a_i\neq \eta \cdot a_i$
. Then by (K2),
$\gamma \cdot a_i\neq \eta \cdot a_i$
. Then by (K2),
![]() $\gamma KH_i\neq \eta KH_i$
. Isometry follows from Lemma 7.10. The preservation of R-value follows directly from the definition of
$\gamma KH_i\neq \eta KH_i$
. Isometry follows from Lemma 7.10. The preservation of R-value follows directly from the definition of
![]() $R^Y$
.
$R^Y$
.
Finally, we verify that for all
![]() $g\in F$
and
$g\in F$
and
![]() $a\in A$
, if
$a\in A$
, if
![]() $g\cdot a\in A$
then
$g\cdot a\in A$
then
Assume
![]() $a=\gamma \cdot a_i$
and
$a=\gamma \cdot a_i$
and
![]() $g\cdot a=\eta \cdot a_i$
for
$g\cdot a=\eta \cdot a_i$
for
![]() $\gamma , \eta \in F$
and
$\gamma , \eta \in F$
and
![]() $1\leq i\leq m$
. Then
$1\leq i\leq m$
. Then
Thus
![]() $\eta ^{-1}g\gamma \in H_i\subseteq KH_i$
, and
$\eta ^{-1}g\gamma \in H_i\subseteq KH_i$
, and
This completes the proof of Theorem 7.8.
We remark that the same method can be used to give a direct proof of Theorem 6.1 (also cf. [Reference Etedadialiabadi and Gao6]).
7.3. The Fraïssé class of actions by automorphisms
In this final subsection we prove that for any semiproper continuous signature
![]() $\mathcal {L}$
the class
$\mathcal {L}$
the class
![]() $\mathcal {C}_{\mathcal {L}}$
defined in Definition 7.1 is a Fraïssé class. The argument follows closely the proof of Theorems 3.9 and 4.8 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]. We give some details for the convenience of the reader. The key fact is the following theorem.
$\mathcal {C}_{\mathcal {L}}$
defined in Definition 7.1 is a Fraïssé class. The argument follows closely the proof of Theorems 3.9 and 4.8 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]. We give some details for the convenience of the reader. The key fact is the following theorem.
Theorem 7.12. Let
![]() $\mathcal {L}$
be a semiproper continuous signature. Then
$\mathcal {L}$
be a semiproper continuous signature. Then
![]() $\mathcal {C}_{\mathcal {L}}$
has the AP.
$\mathcal {C}_{\mathcal {L}}$
has the AP.
Proof Assume
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
are finite groups, and
$\Gamma _2$
are finite groups, and
![]() $\Lambda $
is a subgroup of both
$\Lambda $
is a subgroup of both
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
. Assume
$\Gamma _2$
. Assume
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
are finite continuous
$\mathcal {M}_2$
are finite continuous
![]() $\mathcal {L}$
-structures, and
$\mathcal {L}$
-structures, and
![]() $\mathcal {A}$
a substructure of both
$\mathcal {A}$
a substructure of both
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
. Assume
$\mathcal {M}_2$
. Assume
![]() $\pi _1:\Gamma _1\curvearrowright \mathcal {M}_1$
,
$\pi _1:\Gamma _1\curvearrowright \mathcal {M}_1$
,
![]() $\pi _2:\Gamma _2\curvearrowright \mathcal {M}_2$
and
$\pi _2:\Gamma _2\curvearrowright \mathcal {M}_2$
and
![]() $\tau :\Lambda \curvearrowright \mathcal {A}$
. Furthermore, assume that
$\tau :\Lambda \curvearrowright \mathcal {A}$
. Furthermore, assume that
Let
![]() $\Gamma =\Gamma _1*_{\Lambda }\Gamma _2$
. By Proposition 4.4 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8],
$\Gamma =\Gamma _1*_{\Lambda }\Gamma _2$
. By Proposition 4.4 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8],
![]() $\Gamma $
has the HL-property.
$\Gamma $
has the HL-property.
Since by Theorem 3.8,
![]() ${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
has the SAP, we may obtain a strong amalgam of
${\mathcal {K}^{\mathcal {L}}_{\mathrm {\scriptsize fin}}}$
has the SAP, we may obtain a strong amalgam of
![]() $\mathcal {M}_1$
and
$\mathcal {M}_1$
and
![]() $\mathcal {M}_2$
over
$\mathcal {M}_2$
over
![]() $\mathcal {A}$
, which we denote by
$\mathcal {A}$
, which we denote by
![]() $\mathcal {N}_0$
, such that
$\mathcal {N}_0$
, such that
![]() $\pi _1$
,
$\pi _1$
,
![]() $\pi _2$
,
$\pi _2$
,
![]() $\tau $
are actions respectively on
$\tau $
are actions respectively on
![]() $\mathcal {M}_1$
,
$\mathcal {M}_1$
,
![]() $\mathcal {M}_2$
,
$\mathcal {M}_2$
,
![]() $\mathcal {A}$
as substructures of
$\mathcal {A}$
as substructures of
![]() $\mathcal {N}$
, still satisfying the compatibility condition above. Moreover, by the proof of Theorem 3.8, we may assume
$\mathcal {N}$
, still satisfying the compatibility condition above. Moreover, by the proof of Theorem 3.8, we may assume
![]() $N_0=M_1\cup M_2$
and
$N_0=M_1\cup M_2$
and
![]() $M_1\cap M_2=A$
. Now
$M_1\cap M_2=A$
. Now
![]() $\Lambda $
as a subgroup of both
$\Lambda $
as a subgroup of both
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
acts on
$\Gamma _2$
acts on
![]() $\mathcal {N}_0$
in a natural way, and this action is still by automorphisms.
$\mathcal {N}_0$
in a natural way, and this action is still by automorphisms.
We now inductively define a sequence of extensions
of
![]() $\mathcal {N}_0$
. To define
$\mathcal {N}_0$
. To define
![]() $\mathcal {N}_1$
, apply Lemma 7.4 to the actions
$\mathcal {N}_1$
, apply Lemma 7.4 to the actions
![]() $\Lambda \curvearrowright \mathcal {N}_0$
and
$\Lambda \curvearrowright \mathcal {N}_0$
and
![]() $\Gamma _1\curvearrowright \mathcal {M}_1$
. We obtain
$\Gamma _1\curvearrowright \mathcal {M}_1$
. We obtain
![]() $\mathcal {N}_1$
and an action
$\mathcal {N}_1$
and an action
![]() $\Gamma _1\curvearrowright \mathcal {N}_1$
that is compatible with the actions
$\Gamma _1\curvearrowright \mathcal {N}_1$
that is compatible with the actions
![]() $\Lambda \curvearrowright \mathcal {N}_0$
and
$\Lambda \curvearrowright \mathcal {N}_0$
and
![]() $\Gamma _1\curvearrowright M_1$
. This action also induces an action
$\Gamma _1\curvearrowright M_1$
. This action also induces an action
![]() $\Lambda \curvearrowright \mathcal {N}_1$
. To define
$\Lambda \curvearrowright \mathcal {N}_1$
. To define
![]() $\mathcal {N}_2$
, we apply Lemma 7.4 to this induced action
$\mathcal {N}_2$
, we apply Lemma 7.4 to this induced action
![]() $\Lambda \curvearrowright \mathcal {N}_1$
and
$\Lambda \curvearrowright \mathcal {N}_1$
and
![]() $\Gamma _2\curvearrowright \mathcal {M}_2$
. The result is an extension
$\Gamma _2\curvearrowright \mathcal {M}_2$
. The result is an extension
![]() $\mathcal {N}_2$
together with an action
$\mathcal {N}_2$
together with an action
![]() $\Gamma _2\curvearrowright \mathcal {N}_2$
that is compatible with the actions
$\Gamma _2\curvearrowright \mathcal {N}_2$
that is compatible with the actions
![]() $\Lambda \curvearrowright \mathcal {N}_1$
and
$\Lambda \curvearrowright \mathcal {N}_1$
and
![]() $\Gamma _2\curvearrowright \mathcal {M}_2$
. In general, suppose
$\Gamma _2\curvearrowright \mathcal {M}_2$
. In general, suppose
![]() $\mathcal {N}_{2k}$
has been defined with an action
$\mathcal {N}_{2k}$
has been defined with an action
![]() $\Gamma _2\curvearrowright \mathcal {N}_{2k}$
and
$\Gamma _2\curvearrowright \mathcal {N}_{2k}$
and
![]() $\Gamma _1\curvearrowright N_{2k-1}$
. We apply Lemma 7.4 to the induced action
$\Gamma _1\curvearrowright N_{2k-1}$
. We apply Lemma 7.4 to the induced action
![]() $\Lambda \curvearrowright \mathcal {N}_{2k}$
and the action
$\Lambda \curvearrowright \mathcal {N}_{2k}$
and the action
![]() $\Gamma _1\curvearrowright N_{2k-1}$
to obtain
$\Gamma _1\curvearrowright N_{2k-1}$
to obtain
![]() $\mathcal {N}_{2k+1}$
with an action
$\mathcal {N}_{2k+1}$
with an action
![]() $\Gamma _1\curvearrowright \mathcal {N}_{2k+1}$
that is compatible with the two actions mentioned before. Similarly, apply Lemma 7.4 to the induced action
$\Gamma _1\curvearrowright \mathcal {N}_{2k+1}$
that is compatible with the two actions mentioned before. Similarly, apply Lemma 7.4 to the induced action
![]() $\Lambda \curvearrowright \mathcal {N}_{2k+1}$
and the action
$\Lambda \curvearrowright \mathcal {N}_{2k+1}$
and the action
![]() $\Gamma _2\curvearrowright \mathcal {N}_{2k}$
to obtain
$\Gamma _2\curvearrowright \mathcal {N}_{2k}$
to obtain
![]() $\mathcal {N}_{2k+2}$
and action
$\mathcal {N}_{2k+2}$
and action
![]() $\Gamma _2\curvearrowright \mathcal {N}_{2k+2}$
.
$\Gamma _2\curvearrowright \mathcal {N}_{2k+2}$
.
Let
![]() $\mathcal {N}_\infty =\bigcup _n \mathcal {N}_n$
. Then
$\mathcal {N}_\infty =\bigcup _n \mathcal {N}_n$
. Then
![]() $\Gamma =\Gamma _1*_\Lambda \Gamma _2$
acts on
$\Gamma =\Gamma _1*_\Lambda \Gamma _2$
acts on
![]() $\mathcal {N}_\infty $
naturally, and this action is by automorphisms. We denote this action by
$\mathcal {N}_\infty $
naturally, and this action is by automorphisms. We denote this action by
![]() $\pi $
.
$\pi $
.
Now applying Theorem 7.8 to
![]() $\Gamma \curvearrowright \mathcal {N}_\infty $
,
$\Gamma \curvearrowright \mathcal {N}_\infty $
,
![]() $\mathcal {N}_0$
and
$\mathcal {N}_0$
and
![]() $\Gamma _1\cup \Gamma _2$
, we obtain a finite continuous
$\Gamma _1\cup \Gamma _2$
, we obtain a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
and an action by automorphisms
$\mathcal {N}$
and an action by automorphisms
![]() $\pi ':\Gamma \curvearrowright \mathcal {N}$
such that
$\pi ':\Gamma \curvearrowright \mathcal {N}$
such that
![]() $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
![]() $\mathcal {N}_0$
and for all
$\mathcal {N}_0$
and for all
![]() $\gamma \in \Gamma _1\cup \Gamma _2$
and
$\gamma \in \Gamma _1\cup \Gamma _2$
and
![]() $x\in \mathcal {N}_0$
, if
$x\in \mathcal {N}_0$
, if
![]() $\gamma \cdot _\pi x\in A$
, then
$\gamma \cdot _\pi x\in A$
, then
![]() $\gamma \cdot _\pi x=\gamma \cdot _{\pi '} x$
.
$\gamma \cdot _\pi x=\gamma \cdot _{\pi '} x$
.
Let G be the subgroup of
![]() ${\mathrm {Aut}}(\mathcal {N})$
generated by
${\mathrm {Aut}}(\mathcal {N})$
generated by
![]() $\Gamma _1\cup \Gamma _2$
. Since
$\Gamma _1\cup \Gamma _2$
. Since
![]() $\mathcal {N}$
is finite, so is G. Now the action
$\mathcal {N}$
is finite, so is G. Now the action
![]() $G\curvearrowright \mathcal {N}$
is an amalgam of
$G\curvearrowright \mathcal {N}$
is an amalgam of
![]() $\Gamma _1\curvearrowright \mathcal {M}_1$
and
$\Gamma _1\curvearrowright \mathcal {M}_1$
and
![]() $\Gamma _2\curvearrowright \mathcal {M}_2$
over
$\Gamma _2\curvearrowright \mathcal {M}_2$
over
![]() $\Lambda \curvearrowright \mathcal {A}$
.
$\Lambda \curvearrowright \mathcal {A}$
.
The following theorem implies the JEP for
![]() $\mathcal {C}_{\mathcal {L}}$
.
$\mathcal {C}_{\mathcal {L}}$
.
Theorem 7.13. Let
![]() $\mathcal {L}$
be a semiproper continuous signature. Let
$\mathcal {L}$
be a semiproper continuous signature. Let
![]() $\Gamma , \Lambda $
be groups, let
$\Gamma , \Lambda $
be groups, let
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
be continuous
$\mathcal {N}$
be continuous
![]() $\mathcal {L}$
-pre-structures, and
$\mathcal {L}$
-pre-structures, and
![]() $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
![]() $\mathcal {N}\curvearrowright \mathcal {N}$
are actions by automorphisms. Suppose
$\mathcal {N}\curvearrowright \mathcal {N}$
are actions by automorphisms. Suppose
![]() ${\mathrm {diam}}(M), {\mathrm {diam}}(N)<\infty $
. Then there exists a continuous
${\mathrm {diam}}(M), {\mathrm {diam}}(N)<\infty $
. Then there exists a continuous
![]() $\mathcal {L}$
-pre-structure
$\mathcal {L}$
-pre-structure
![]() $\mathcal {P}$
, an action by automorphisms
$\mathcal {P}$
, an action by automorphisms
![]() $\Gamma \times \Lambda \curvearrowright \mathcal {P}$
and embeddings i from
$\Gamma \times \Lambda \curvearrowright \mathcal {P}$
and embeddings i from
![]() $\Gamma \curvearrowright \mathcal {M}$
into
$\Gamma \curvearrowright \mathcal {M}$
into
![]() $\Gamma \times \Lambda \curvearrowright \mathcal {P}$
and j from
$\Gamma \times \Lambda \curvearrowright \mathcal {P}$
and j from
![]() $\Lambda \curvearrowright \mathcal {N}$
into
$\Lambda \curvearrowright \mathcal {N}$
into
![]() $\Gamma \times \Lambda \curvearrowright \mathcal {P}$
. In particular, the JEP holds for
$\Gamma \times \Lambda \curvearrowright \mathcal {P}$
. In particular, the JEP holds for
![]() $\mathcal {C}_{\mathcal {L}}$
.
$\mathcal {C}_{\mathcal {L}}$
.
Proof Let X be the disjoint union of M and N. Let
![]() $\delta \geq {\mathrm {diam}}(M), {\mathrm {diam}}(N)$
and for all n-ary
$\delta \geq {\mathrm {diam}}(M), {\mathrm {diam}}(N)$
and for all n-ary
![]() $R\in \mathcal {L}$
and all
$R\in \mathcal {L}$
and all
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $\delta \geq \sup I_{R,i}$
. Then define a metric
$\delta \geq \sup I_{R,i}$
. Then define a metric
![]() $d^X$
on X by
$d^X$
on X by
 $$ \begin{align*}d^X(x, y)=\left\{\begin{array}{@{}ll} d^{M}(x, y), & \mbox{ if}\ x, y\in M, \\ d^N(x,y), & \mbox{ if}\ x, y\in N, \\ \delta, & \mbox{ otherwise.} \end{array}\right. \end{align*} $$
$$ \begin{align*}d^X(x, y)=\left\{\begin{array}{@{}ll} d^{M}(x, y), & \mbox{ if}\ x, y\in M, \\ d^N(x,y), & \mbox{ if}\ x, y\in N, \\ \delta, & \mbox{ otherwise.} \end{array}\right. \end{align*} $$
For every
![]() $R\in \mathcal {L}$
,
$R\in \mathcal {L}$
,
![]() $R^X$
is naturally defined on
$R^X$
is naturally defined on
It is clear that
![]() $\mathcal {X}=(X, d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
$\mathcal {X}=(X, d^X, (R^X)_{R\in \mathcal {L}})$
is a partially defined continuous
![]() $\mathcal {L}$
-pre-structure. Then by Lemma 3.7,
$\mathcal {L}$
-pre-structure. Then by Lemma 3.7,
![]() $\mathcal {X}$
has a conservative extension
$\mathcal {X}$
has a conservative extension
![]() $\mathcal {P}$
. It is easy to see that
$\mathcal {P}$
. It is easy to see that
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
embed into
$\mathcal {N}$
embed into
![]() $\mathcal {P}$
as substructures.
$\mathcal {P}$
as substructures.
Define an action
![]() $\Gamma \times \Lambda \curvearrowright \mathcal {P}$
by
$\Gamma \times \Lambda \curvearrowright \mathcal {P}$
by
 $$ \begin{align*}(\gamma, \lambda)\cdot x=\left\{\begin{array}{@{}ll}\gamma(x), & \mbox{ if}\ x\in M, \\ \lambda(x), & \mbox{ if}\ x\in N.\end{array}\right.\end{align*} $$
$$ \begin{align*}(\gamma, \lambda)\cdot x=\left\{\begin{array}{@{}ll}\gamma(x), & \mbox{ if}\ x\in M, \\ \lambda(x), & \mbox{ if}\ x\in N.\end{array}\right.\end{align*} $$
It is easy to see that this action is by automorphisms on
![]() $\mathcal {P}$
. Also,
$\mathcal {P}$
. Also,
![]() $\Gamma \curvearrowright \mathcal {M}$
and
$\Gamma \curvearrowright \mathcal {M}$
and
![]() $\Lambda \curvearrowright \mathcal {N}$
embed into
$\Lambda \curvearrowright \mathcal {N}$
embed into
![]() $\Gamma \times \Lambda \curvearrowright \mathcal {P}$
.
$\Gamma \times \Lambda \curvearrowright \mathcal {P}$
.
Corollary 7.14. Let
![]() $\mathcal {L}$
be a semiproper continuous signature. Then
$\mathcal {L}$
be a semiproper continuous signature. Then
![]() $\mathcal {C}_{\mathcal {L}}$
is a Fraïssé class.
$\mathcal {C}_{\mathcal {L}}$
is a Fraïssé class.
8. Dense locally finite subgroups of the automorphism groups
In this last section of the paper we prove that Hall’s universal locally finite group
![]() $\mathbb {H}$
can be embedded as a dense subgroup of
$\mathbb {H}$
can be embedded as a dense subgroup of
![]() ${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
for proper
${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
for proper
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
P. Hall first constructed
![]() $\mathbb {H}$
in [Reference Hall9] and proved that it is the unique countable locally finite group that is universal for all finite groups and is ultrahomogeneous. He also showed that
$\mathbb {H}$
in [Reference Hall9] and proved that it is the unique countable locally finite group that is universal for all finite groups and is ultrahomogeneous. He also showed that
![]() $\mathbb {H}$
is universal for all countable locally finite groups. It is well known that
$\mathbb {H}$
is universal for all countable locally finite groups. It is well known that
![]() $\mathbb {H}$
is the Fraïssé limit of the countable Fraïssé class of all finite groups. It was shown in [Reference Etedadialiabadi, Gao, Le Maître and Melleray8] that
$\mathbb {H}$
is the Fraïssé limit of the countable Fraïssé class of all finite groups. It was shown in [Reference Etedadialiabadi, Gao, Le Maître and Melleray8] that
![]() $\mathbb {H}$
embeds as a dense subgroup of the isometry group of
$\mathbb {H}$
embeds as a dense subgroup of the isometry group of
![]() $\mathbb {U}_\Delta $
for any countable distance value set
$\mathbb {U}_\Delta $
for any countable distance value set
![]() $\Delta $
; the same is true for the isometry group of
$\Delta $
; the same is true for the isometry group of
![]() $\mathbb {U}$
(Theorems 3.14 and 3.16 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]).
$\mathbb {U}$
(Theorems 3.14 and 3.16 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8]).
Here we consider first a semiproper continuous signature
![]() $\mathcal {L}$
and a countable good value pair
$\mathcal {L}$
and a countable good value pair
![]() $(\Delta , V)$
for
$(\Delta , V)$
for
![]() $\mathcal {L}$
. By Theorem 5.5, the class
$\mathcal {L}$
. By Theorem 5.5, the class
![]() $\mathcal {K}_{(\Delta ,V)}$
of all finite
$\mathcal {K}_{(\Delta ,V)}$
of all finite
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-structures is a countable Fraïssé class. We consider the subclass of
$\mathcal {L}$
-structures is a countable Fraïssé class. We consider the subclass of
![]() $\mathcal {C}_{\mathcal {L}}$
defined as
$\mathcal {C}_{\mathcal {L}}$
defined as
 $$ \begin{align*}\mathcal{C}_{(\Delta,V)}&=\mbox{ the subclass of}\ \mathcal{C}_{\mathcal{L}}\ \mbox{ consisting of actions by automorphisms}\ \Gamma\curvearrowright \mathcal{M} \\& \quad\ \ \mbox{ where}\ \Gamma\ \mbox{is finite and}\ \mathcal{M}\in\mathcal{K}_{(\Delta, V)}. \end{align*} $$
$$ \begin{align*}\mathcal{C}_{(\Delta,V)}&=\mbox{ the subclass of}\ \mathcal{C}_{\mathcal{L}}\ \mbox{ consisting of actions by automorphisms}\ \Gamma\curvearrowright \mathcal{M} \\& \quad\ \ \mbox{ where}\ \Gamma\ \mbox{is finite and}\ \mathcal{M}\in\mathcal{K}_{(\Delta, V)}. \end{align*} $$
The entire Section 7 can be repeated for
![]() $\mathcal {C}_{(\Delta ,V)}$
to give the following result.
$\mathcal {C}_{(\Delta ,V)}$
to give the following result.
Theorem 8.1. Let
![]() $\mathcal {L}$
be a semiproper continuous signature and let
$\mathcal {L}$
be a semiproper continuous signature and let
![]() $(\Delta , V)$
be a countable good value pair for
$(\Delta , V)$
be a countable good value pair for
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() $\mathcal {C}_{(\Delta , V)}$
is a countable Fraïssé class.
$\mathcal {C}_{(\Delta , V)}$
is a countable Fraïssé class.
Proof The proof is identical to the proof of Corollary 7.14.
Let
![]() $\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
be the Fraïssé limit of
$\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
be the Fraïssé limit of
![]() $\mathcal {C}_{(\Delta , V)}$
. Then
$\mathcal {C}_{(\Delta , V)}$
. Then
![]() $\mathcal {M}_\infty $
is a countable
$\mathcal {M}_\infty $
is a countable
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-pre-structure,
$\mathcal {L}$
-pre-structure,
![]() $\Gamma _\infty $
is a locally finite group, and the action is by automorphisms. By the arguments for Theorem 3.14 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8], we prove the following lemmas.
$\Gamma _\infty $
is a locally finite group, and the action is by automorphisms. By the arguments for Theorem 3.14 of [Reference Etedadialiabadi, Gao, Le Maître and Melleray8], we prove the following lemmas.
Lemma 8.2.
![]() $\mathcal {M}_\infty $
is isomorphic to
$\mathcal {M}_\infty $
is isomorphic to
![]() $\mathbb {U}_{(\Delta ,V)}$
.
$\mathbb {U}_{(\Delta ,V)}$
.
Proof
![]() $\mathbb {U}_{(\Delta , V)}$
is is the unique countable continuous
$\mathbb {U}_{(\Delta , V)}$
is is the unique countable continuous
![]() $\mathcal {L}$
-pre-structure with the
$\mathcal {L}$
-pre-structure with the
![]() $(\Delta , V)$
-Urysohn property: given any finite
$(\Delta , V)$
-Urysohn property: given any finite
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
, a one-point extension
$\mathcal {M}$
, a one-point extension
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {M}$
that is
$\mathcal {M}$
that is
![]() $(\Delta , V)$
-valued, and an isomorphic embedding
$(\Delta , V)$
-valued, and an isomorphic embedding
![]() $\varphi $
from
$\varphi $
from
![]() $\mathcal {M}$
into
$\mathcal {M}$
into
![]() $\mathbb {U}_{(\Delta , V)}$
, there is an isomorphic embedding
$\mathbb {U}_{(\Delta , V)}$
, there is an isomorphic embedding
![]() $\psi $
from
$\psi $
from
![]() $\mathcal {N}$
into
$\mathcal {N}$
into
![]() $\mathbb {U}_{(\Delta ,V)}$
such that
$\mathbb {U}_{(\Delta ,V)}$
such that
![]() $\psi \,{\!\upharpoonright \!}\,\, M=\varphi $
.
$\psi \,{\!\upharpoonright \!}\,\, M=\varphi $
.
We verify that
![]() $\mathcal {M}_\infty $
has this property. It is clear that
$\mathcal {M}_\infty $
has this property. It is clear that
![]() $\mathcal {M}_\infty $
is
$\mathcal {M}_\infty $
is
![]() $(\Delta , V)$
-valued. Suppose
$(\Delta , V)$
-valued. Suppose
![]() $A\subseteq \mathcal {M}_\infty $
and let
$A\subseteq \mathcal {M}_\infty $
and let
![]() $\mathcal {A}_x$
be a
$\mathcal {A}_x$
be a
![]() $(\Delta , V)$
-valued one-point extension of
$(\Delta , V)$
-valued one-point extension of
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $\Gamma $
be the trivial group. Then
$\Gamma $
be the trivial group. Then
![]() $\Gamma \curvearrowright \mathcal {A}$
embeds into
$\Gamma \curvearrowright \mathcal {A}$
embeds into
![]() $\Gamma \curvearrowright \mathcal {A}_x$
trivially. By the universality and ultrahomogeneity of
$\Gamma \curvearrowright \mathcal {A}_x$
trivially. By the universality and ultrahomogeneity of
![]() $\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
, we obtain an embedding
$\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
, we obtain an embedding
![]() $\varphi $
of
$\varphi $
of
![]() $\Gamma \curvearrowright \mathcal {A}_x$
into
$\Gamma \curvearrowright \mathcal {A}_x$
into
![]() $\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
such that
$\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
such that
![]() $\varphi \,{\!\upharpoonright \!}\,\, M$
is the identity. Thus
$\varphi \,{\!\upharpoonright \!}\,\, M$
is the identity. Thus
![]() $\varphi $
witnesses the the
$\varphi $
witnesses the the
![]() $(\Delta , V)$
-Urysohn property of
$(\Delta , V)$
-Urysohn property of
![]() $\mathcal {M}_\infty $
.
$\mathcal {M}_\infty $
.
Lemma 8.3.
![]() $\Gamma _\infty $
acts faithfully on
$\Gamma _\infty $
acts faithfully on
![]() $\mathcal {M}_\infty $
.
$\mathcal {M}_\infty $
.
Proof Let
![]() $g\in \Gamma _\infty $
be a non-identity element. Let
$g\in \Gamma _\infty $
be a non-identity element. Let
![]() $\Gamma $
be the subgroup of
$\Gamma $
be the subgroup of
![]() $\Gamma _\infty $
generated by g. Since
$\Gamma _\infty $
generated by g. Since
![]() $\Gamma _\infty $
is locally finite,
$\Gamma _\infty $
is locally finite,
![]() $\Gamma $
is finite. Consider the finite continuous
$\Gamma $
is finite. Consider the finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
defined as follows. Let
$\mathcal {M}$
defined as follows. Let
![]() $\delta \in \Delta $
. Let
$\delta \in \Delta $
. Let
![]() $M=\Gamma $
. Define
$M=\Gamma $
. Define
![]() $d^M(x,y)=\delta $
for any
$d^M(x,y)=\delta $
for any
![]() $x\neq y\in M$
. For any
$x\neq y\in M$
. For any
![]() $R\in \mathcal {L}$
, define
$R\in \mathcal {L}$
, define
![]() $R^M$
to be identically
$R^M$
to be identically
![]() $0$
. Then
$0$
. Then
![]() $\mathcal {M}$
is a finite
$\mathcal {M}$
is a finite
![]() $(\Delta , V)$
-valued continuous
$(\Delta , V)$
-valued continuous
![]() $\mathcal {L}$
-structure and the left multiplication action
$\mathcal {L}$
-structure and the left multiplication action
![]() $\Gamma \curvearrowright \mathcal {M}$
is an action by automorphisms. By the universality and ultrahomogeneity of
$\Gamma \curvearrowright \mathcal {M}$
is an action by automorphisms. By the universality and ultrahomogeneity of
![]() $\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
, we know that
$\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
, we know that
![]() $\mathcal {M}$
can be realized as a substructure of
$\mathcal {M}$
can be realized as a substructure of
![]() $\mathcal {M}_\infty $
. If follows that there is
$\mathcal {M}_\infty $
. If follows that there is
![]() $x\in \mathcal {M}_\infty $
such that
$x\in \mathcal {M}_\infty $
such that
![]() $g\cdot x\neq x$
.
$g\cdot x\neq x$
.
Lemma 8.4.
![]() $\Gamma _\infty $
is isomorphic to
$\Gamma _\infty $
is isomorphic to
![]() $\mathbb {H}$
.
$\mathbb {H}$
.
Proof
![]() $\mathbb {H}$
is the unique countable locally finite group with the following extension property: given any finite groups
$\mathbb {H}$
is the unique countable locally finite group with the following extension property: given any finite groups
![]() $G\leq H$
and a group isomorphic embedding
$G\leq H$
and a group isomorphic embedding
![]() $\varphi $
from G into
$\varphi $
from G into
![]() $\mathbb {H}$
, there is a group isomorphic embedding
$\mathbb {H}$
, there is a group isomorphic embedding
![]() $\psi $
from H into
$\psi $
from H into
![]() $\mathbb {H}$
such that
$\mathbb {H}$
such that
![]() $\psi \,{\!\upharpoonright \!}\,\, G=\varphi $
.
$\psi \,{\!\upharpoonright \!}\,\, G=\varphi $
.
We verify that
![]() $\Gamma _\infty $
has this property. Assume
$\Gamma _\infty $
has this property. Assume
![]() $G, H, \varphi $
are given. Consider the trivial structure
$G, H, \varphi $
are given. Consider the trivial structure
![]() $\mathcal {M}$
which is a singleton and such that all relations symbols are interpreted as identically
$\mathcal {M}$
which is a singleton and such that all relations symbols are interpreted as identically
![]() $0$
functions. Then by the universality and ultrahomogeneity of
$0$
functions. Then by the universality and ultrahomogeneity of
![]() $\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
there is an embedding
$\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
there is an embedding
![]() $\psi $
of
$\psi $
of
![]() $H\curvearrowright \mathcal {M}$
into
$H\curvearrowright \mathcal {M}$
into
![]() $\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
such that
$\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
such that
![]() $\psi \,{\!\upharpoonright \!}\,\, G=\varphi $
. This proves the extension property as required.
$\psi \,{\!\upharpoonright \!}\,\, G=\varphi $
. This proves the extension property as required.
Since
![]() $\mathcal {M}_\infty $
is countable, we equip
$\mathcal {M}_\infty $
is countable, we equip
![]() $\mathcal {M}_\infty $
with the discrete topology and
$\mathcal {M}_\infty $
with the discrete topology and
![]() ${\mathrm {Aut}}(\mathcal {M}_\infty )$
with the corresponding pointwise convergence topology. Thus
${\mathrm {Aut}}(\mathcal {M}_\infty )$
with the corresponding pointwise convergence topology. Thus
![]() ${\mathrm { Aut}}(\mathcal {M}_\infty )$
becomes a Polish group. In fact, it is isomorphic to a closed subgroup of
${\mathrm { Aut}}(\mathcal {M}_\infty )$
becomes a Polish group. In fact, it is isomorphic to a closed subgroup of
![]() $S_\infty $
, the infinite permutation group.
$S_\infty $
, the infinite permutation group.
Lemma 8.5.
![]() $\Gamma _\infty $
is dense in
$\Gamma _\infty $
is dense in
![]() ${\mathrm {Aut}}(\mathcal {M}_\infty )$
.
${\mathrm {Aut}}(\mathcal {M}_\infty )$
.
Proof Let
![]() $g\in {\mathrm {Aut}}(\mathcal {M}_\infty )$
and let
$g\in {\mathrm {Aut}}(\mathcal {M}_\infty )$
and let
![]() $A\subseteq M_\infty $
be finite. We need to find a
$A\subseteq M_\infty $
be finite. We need to find a
![]() ${\gamma \in \Gamma _\infty} $
such that for every
${\gamma \in \Gamma _\infty} $
such that for every
![]() $a\in A$
,
$a\in A$
,
![]() $g(a)=\gamma \cdot a$
. Let
$g(a)=\gamma \cdot a$
. Let
![]() $\Gamma $
be the subgroup of
$\Gamma $
be the subgroup of
![]() ${\mathrm {Aut}}(\mathcal {M}_\infty )$
generated by g.
${\mathrm {Aut}}(\mathcal {M}_\infty )$
generated by g.
Suppose first
![]() $\Gamma $
is finite. Then let
$\Gamma $
is finite. Then let
![]() $B=\Gamma (A)$
. B is finite, and
$B=\Gamma (A)$
. B is finite, and
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $\mathcal {B}$
by automorphisms by definition. By the universality and ultrahomogeneity of
$\mathcal {B}$
by automorphisms by definition. By the universality and ultrahomogeneity of
![]() ${\Gamma _\infty \curvearrowright \mathcal {M}_\infty} $
, we may realize
${\Gamma _\infty \curvearrowright \mathcal {M}_\infty} $
, we may realize
![]() $\Gamma $
as a subgroup of
$\Gamma $
as a subgroup of
![]() $\Gamma _\infty $
. This gives a
$\Gamma _\infty $
. This gives a
![]() $\gamma \in \Gamma _\infty $
such that for every
$\gamma \in \Gamma _\infty $
such that for every
![]() $a\in A$
,
$a\in A$
,
![]() $g(a)=\gamma \cdot a$
.
$g(a)=\gamma \cdot a$
.
Next suppose
![]() $\Gamma $
is infinite. Then
$\Gamma $
is infinite. Then
![]() $\Gamma =\langle g\rangle $
is a free abelian group, and by a theorem of Herwig–Lascar (Theorem 3.3 of [Reference Herwig and Lascar10]),
$\Gamma =\langle g\rangle $
is a free abelian group, and by a theorem of Herwig–Lascar (Theorem 3.3 of [Reference Herwig and Lascar10]),
![]() $\Gamma $
has the HL-property. Consider
$\Gamma $
has the HL-property. Consider
![]() $F=\{g\}$
and
$F=\{g\}$
and
![]() $B=A\cup g(A)$
. By Theorem 7.8 there is a finite continuous
$B=A\cup g(A)$
. By Theorem 7.8 there is a finite continuous
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {N}$
and an action
$\mathcal {N}$
and an action
![]() $\pi :\Gamma \curvearrowright \mathcal {N}$
such that
$\pi :\Gamma \curvearrowright \mathcal {N}$
such that
![]() $\mathcal {N}$
is an extension of
$\mathcal {N}$
is an extension of
![]() $\mathcal {B}$
and for all
$\mathcal {B}$
and for all
![]() $a\in A$
,
$a\in A$
,
![]() $g\cdot _{\pi } a=g(a)$
. Let
$g\cdot _{\pi } a=g(a)$
. Let
![]() $\Lambda $
be the subgroup of
$\Lambda $
be the subgroup of
![]() ${\mathrm {Aut}}(\mathcal {N})$
generated by g. Since
${\mathrm {Aut}}(\mathcal {N})$
generated by g. Since
![]() $\mathcal {N}$
is finite,
$\mathcal {N}$
is finite,
![]() $\Lambda $
is finite. By the universality and ultrahomogeneity of
$\Lambda $
is finite. By the universality and ultrahomogeneity of
![]() $\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
, we may realize
$\Gamma _\infty \curvearrowright \mathcal {M}_\infty $
, we may realize
![]() $\Lambda $
as a subgroup of
$\Lambda $
as a subgroup of
![]() $\Gamma _\infty $
and
$\Gamma _\infty $
and
![]() $\mathcal {N}$
as a substructure of
$\mathcal {N}$
as a substructure of
![]() $\mathcal {M}_\infty $
extending
$\mathcal {M}_\infty $
extending
![]() $\mathcal {B}$
. This gives a
$\mathcal {B}$
. This gives a
![]() $\gamma \in \Gamma _\infty $
such that for every
$\gamma \in \Gamma _\infty $
such that for every
![]() $a\in A$
,
$a\in A$
,
![]() $g(a)=\gamma \cdot a$
.
$g(a)=\gamma \cdot a$
.
Putting these lemmas together, we have proved the following theorem.
Theorem 8.6. Let
![]() $\mathcal {L}$
be a semiproper continuous signature and let
$\mathcal {L}$
be a semiproper continuous signature and let
![]() $(\Delta , V)$
be a countable good value pair for
$(\Delta , V)$
be a countable good value pair for
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() ${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
contains
${\mathrm {Aut}}(\mathbb {U}_{(\Delta , V)})$
contains
![]() $\mathbb {H}$
as a dense subgroup.
$\mathbb {H}$
as a dense subgroup.
We have the following corollary.
Corollary 8.7. Let
![]() $\mathcal {L}$
be a proper continuous signature. Then
$\mathcal {L}$
be a proper continuous signature. Then
![]() ${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
contains
${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
contains
![]() $\mathbb {H}$
as a dense subgroup.
$\mathbb {H}$
as a dense subgroup.
Proof By Theorem 8.6 we have that
![]() ${\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}})$
contains
${\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}})$
contains
![]() $\mathbb {H}$
as a dense subgroup. Since
$\mathbb {H}$
as a dense subgroup. Since
![]() $\mathbb {U}_{\mathcal {L}}$
is isomorphic to the completion of
$\mathbb {U}_{\mathcal {L}}$
is isomorphic to the completion of
![]() $\mathbb {QU}_{\mathcal {L}}$
by Theorem 5.6, there is an isomorphic embedding
$\mathbb {QU}_{\mathcal {L}}$
by Theorem 5.6, there is an isomorphic embedding
![]() $i: \mathbb {QU}_{\mathcal {L}}\to \mathbb {U}_{\mathcal {L}}$
with a dense range. This induces a group isomorphic embedding
$i: \mathbb {QU}_{\mathcal {L}}\to \mathbb {U}_{\mathcal {L}}$
with a dense range. This induces a group isomorphic embedding
![]() $\eta : {\mathrm { Aut}}(\mathbb {QU}_{\mathcal {L}})\to {\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
. By Theorem 5.8,
$\eta : {\mathrm { Aut}}(\mathbb {QU}_{\mathcal {L}})\to {\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
. By Theorem 5.8,
![]() $\eta ({\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}}))$
is dense in
$\eta ({\mathrm {Aut}}(\mathbb {QU}_{\mathcal {L}}))$
is dense in
![]() ${\mathrm { Aut}}(\mathbb {U}_{\mathcal {L}})$
. It is easy to see that
${\mathrm { Aut}}(\mathbb {U}_{\mathcal {L}})$
. It is easy to see that
![]() $\eta $
is continuous. Thus
$\eta $
is continuous. Thus
![]() $\eta (\mathbb {H})$
is a dense subgroup of
$\eta (\mathbb {H})$
is a dense subgroup of
![]() ${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
isomorphic to
${\mathrm {Aut}}(\mathbb {U}_{\mathcal {L}})$
isomorphic to
![]() $\mathbb {H}$
.
$\mathbb {H}$
.
Funding
The first author acknowledges the partial support of his research by the National Natural Science Foundation of China (NSFC; Grant Nos. 12250710128 and 12271263). Research of the second author was partially supported by the Innovation and Entrepreneurship Training Program for College Students of Tianjin (Grant No. 202210055334).