Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T18:11:18.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Amalgamations preserving ℵ1-categoricity

Published online by Cambridge University Press:  12 March 2014

Anand Pillay  and
Akito Tsuboi
Anand Pillay
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1409 West Green Street, Altegeld Hall, Urbana, IL 61801, USA, E-mail: pillay@symcom.math.uiuc.edu
Akito Tsuboi
Affiliation:
Institute of Mathematics, University of Tsukuba, Ibaraki 305, Japan, E-mail: tsuboi@sakura.cc.tsukuba.ac.jp
Get access Rights & Permissions [Opens in a new window]

Extract

Let L0, L1 and L2 be countable languages with L ∩ L1 = L0. Let M0 be an L0-structure and Mi, an expansion of M0 to an Li,-structure (i = 1,2). We will call an L1 ∪ L2-structure M an amalgamation of M1 and M2 if M∣Li ≅ Mi, (i = 1,2). Let's consider the following problem.

(*) Suppose that both M1 and M2 belong to the class 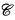. Can we always find an amalgamation M in ?

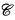Of course the existence of such an amalgamation depends on the class L. Some examples of 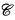and the answers are given below.

1. 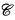= Countably saturated strongly minimal structures with the DMP In [3], Hrushovski showed that any two strongly minimal theories formulated in totally different languages have a common extension which is still strongly minimal and with the DMP (DMP is the property that states that if a point 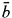is sufficiently close to ā, then φ(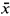, 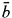) has the same rank and the same degree as φ(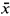, ā).) His proof essentially shows that if L0 = ∅ then any two countably saturated strongly minimal structures with the DMP have a strongly minimal amalgamation. Also he gave an example that shows the condition L0 = ∅ is necessary.

2. 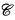= ℵ1-categorical countable structures. Let M1 be the structure (ℚ, +) and let M2 be the {E, F}-structure defined by: (i) E is an equivalence relation which divides the universe into two infinite classes A and B, (ii) F is a bijection between A and B.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 4 , December 1997 , pp. 1070 - 1074
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Evans, D. M. and Hrushovski, E., On the automorphism groups of finite covers, Annals of Pure and Applied Logic, vol. 62 (1993), pp. 83–112.CrossRefGoogle Scholar
[2]Hrushovski, E., Totally categorical structures, Transactions of the American Mathematical Society, vol. 313 (1989), pp. 131–159.CrossRefGoogle Scholar
[3]Hrushovski, E., Strongly minimal expansions of algebraically closed fields, Israel Journal of Mathematics, vol. 79 (1992), pp. 129–151.CrossRefGoogle Scholar
[4]Hrushovski, E. and Pillay, A., Groups definable in local fields and pseudo-finite fields, Israel Journal of Mathematics, vol. 85 (1994), pp. 203–262.CrossRefGoogle Scholar
[5]Pillay, A., Some remarks on modular regular types, this Journal, vol. 56 (1991), pp. 1003–1011.Google Scholar
[6]Schmerl, J. H., Decidability and ℵ0-categoricity of theories of partially ordered sets, this Journal, vol. 45 (1980), pp. 585–611.Google Scholar