Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T20:08:08.354Z Has data issue: false hasContentIssue false
  • English
  • Français

An elementary definability theorem for first order logic

Published online by Cambridge University Press:  12 March 2014

C. Butz  and
I. Moerdijk
C. Butz
Affiliation:
Brics, Computer Science Department, Aarhus University, NY Munkegade, Building 540, DK-8000 Århus C, Denmark E-mail: butz@brics.dk
I. Moerdijk
Affiliation:
Mathematisch Instituut, Universiteit Utrecht, Postbus 80.010, NL-3508 TA Utrecht, The, Netherlands E-mail: moerdijk@math.uu.nl
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, we will present a definability theorem for first order logic. This theorem is very easy to state, and its proof only uses elementary tools. To explain the theorem, let us first observe that if M is a model of a theory T in a language 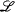, then, clearly, any definable subset S ⊂ M (i.e., a subset S = {a ∣ M ⊨ φ(a)} defined by some formula φ) is invariant under all automorphisms of M. The same is of course true for subsets of Mn defined by formulas with n free variables.

Our theorem states that, if one allows Boolean valued models, the converse holds. More precisely, for any theory T we will construct a Boolean valued model M, in which precisely the T -provable formulas hold, and in which every (Boolean valued) subset which is invariant under all automorphisms of M is definable by a formula .

Our presentation is entirely selfcontained, and only requires familiarity with the most elementary properties of model theory. In particular, we have added a first section in which we review the basic definitions concerning Boolean valued models.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 3 , September 1999 , pp. 1028 - 1036
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Beth, E. W., On Padoa's method in the theory of definition, Nederl Acad. Wetensch. Proc. Ser. A, vol. 56 (1953), pp. 330–339.Google Scholar
[2] Butz, C. and Johnstone, P. T.,Classifying toposes for first order theories, Annals of Pure and Applied Logic, vol. 91 (1998), pp. 33–58.Google Scholar
[3] Burz, C. and Moerdijk, I., Representing topoi by topological groupoids, Journal of Pure and Applied Algebra, vol. 130 (1998), pp. 223–235.Google Scholar
[4] Freyd, P., All topoi are localic or why permutation models prevail, Journal of Pure and Applied Algebra, vol. 46 (1987), pp. 49–58.Google Scholar
[5] Hodges, W., Model theory, Cambridge University Press, Cambridge, 1993.Google Scholar
[6] Koppelberg, S., Booleschewertige Logik, Jber. d. dt. Math.-Verein, vol. 87 (1985), pp. 19–38.Google Scholar
[7] Kueker, D. W., Definability, automorphisms, and infinitary languages, The syntax and semantics of infinitary languages (Barwise, K. J., editor), Lecture Notes in Mathematics, no. 72, Springer-Verlag, Berlin, 1968, pp. 152–165.Google Scholar
[8] Lane, S. Mac and Moerdijk, I.,Sheaves in geometry and logic, Springer-Verlag, New York, 1992.Google Scholar
[9] Palmgren, E., Constructive sheaf semantics, Mathematical Logic Quarterly, vol. 43 (1997), pp. 321–327.Google Scholar
[10] Scott, D., Logic with denumerably long formulas and finite strings of quantifiers, The theory of models (Addison, J. W., Henkin, L. A., and Tarski, A., editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
[11] Svenonius, L., A theorem on permutations in models, Theoria, vol. 25 (1959), pp. 173–178.Google Scholar