Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T17:42:17.578Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXISTENTIAL ∅-DEFINITION OF 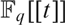$F_q [[t]]$ IN 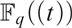$F_q \left( t \right)$

Published online by Cambridge University Press:  12 December 2014

WILL ANSCOMBE  and
JOCHEN KOENIGSMANN
WILL ANSCOMBE
Affiliation:
SCHOOL OF MATHEMATICS UNIVERSITY OF LEEDS LEEDS, LS2 9JT, UKE-mail: w.g.anscombe@leeds.ac.uk
JOCHEN KOENIGSMANN
Affiliation:
MATHEMATICAL INSTITUTE RADCLIFFE OBSERVATORY SITE WOODSTOCK ROAD OXFORD, OX2 6GG, UKE-mail: koenigsmann@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the valuation ring 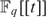$F_q [[t]]$ in the local field 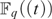$F_q \left( t \right)$ is existentially definable in the language of rings with no parameters. The method is to use the definition of the henselian topology following the work of Prestel-Ziegler to give an ∃-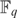$F_q $-definable bounded neighbouhood of 0. Then we “tweak” this set by subtracting, taking roots, and applying Hensel’s Lemma in order to find an ∃-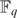$F_q $-definable subset of 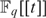$F_q [[t]]$ which contains 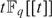$tF_q [[t]]$. Finally, we use the fact that 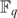$F_q $ is defined by the formula 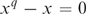$x^q - x = 0$ to extend the definition to the whole of 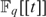$F_q [[t]]$ and to rid the definition of parameters.

Several extensions of the theorem are obtained, notably an ∃-∅-definition of the valuation ring of a nontrivial valuation with divisible value group.

Keywords

Valuationshenselian valued fieldsdefinable valuationsmodel theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 4 , December 2014 , pp. 1336 - 1343
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ax, James, On the undecidability of power series fields. Proceedings of the American Mathematical Society, vol. 16 (1965), p. 846.Google Scholar
Cluckers, Raf, Derakhshan, Jamshid, Leenknegt, Eva, and Macintyre, Angus, Uniformly defining valuation rings in henselian valued fields with finite and pseudo-finite residue field. Annals of Pure and Applied Logic, vol.164 (2013), pp. 1236–1246.Google Scholar
Denef, Jan and Schoutens, Hans, On the decidability of the existential theory of $F_q [[t]]$. Fields Institute Communications, vol. 33 (2003), pp. 43–60.Google Scholar
Koenigsmann, Jochen, Elementary characterization of fields by their absolute Galois group. Siberian Advances in Mathematics, vol. 14 (2004), pp. 16–42.Google Scholar
Macintyre, Angus, On definable subsets of p-adic fields, this Journal, vol. 41 (1976), pp. 605–610.Google Scholar
Prestel, Alexander, Algebraic number fields elementarily determined by their absolute Galois group. Israel Journal of Mathematics, vol. 73 (1991), no. 2, pp. 199–205.Google Scholar
Prestel, Alexander and Ziegler, Martin, Model-theoretic methods in the theory of topological fields. Journal für die Reine und Angewandte Mathematik, vol. 299 (1978), no. 300, pp. 318–341.Google Scholar