Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Larson, Paul
and
Todorcevic, Stevo
2001.
Katetov’s problem.
Transactions of the American Mathematical Society,
Vol. 354,
Issue. 5,
p.
1783.
Tall, Franklin D.
2005.
Problems arising from Balogh's “Locally nice spaces under Martin's Axiom”.
Topology and its Applications,
Vol. 151,
Issue. 1-3,
p.
215.
Larson, Paul
2005.
Saturation, Suslin trees and meager sets.
Archive for Mathematical Logic,
Vol. 44,
Issue. 5,
p.
581.
Yorioka, Teruyuki
2006.
ℙmax variations related to slaloms.
MLQ,
Vol. 52,
Issue. 2,
p.
203.
YORIOKA, Teruyuki
2009.
Forcing Axioms and Ω-logic.
Journal of the Japan Association for Philosophy of Science,
Vol. 36,
Issue. 2,
p.
45.
Larson, Paul B.
2010.
Handbook of Set Theory.
p.
2121.
Scharfenberger-Fabian, Gido
2011.
Souslin algebra embeddings.
Archive for Mathematical Logic,
Vol. 50,
Issue. 1-2,
p.
75.
Martinez-Ranero, Carlos
2013.
Gap structure after forcing with a coherent Souslin tree.
Archive for Mathematical Logic,
Vol. 52,
Issue. 3-4,
p.
435.
Larson, Paul
and
Tall, Franklin D.
2014.
On the Hereditary Paracompactness of Locally Compact, Hereditarily Normal Spaces.
Canadian Mathematical Bulletin,
Vol. 57,
Issue. 3,
p.
579.
Tall, Franklin D.
2014.
PFA(S)[S]and locally compact normal spaces.
Topology and its Applications,
Vol. 162,
Issue. ,
p.
100.
Yorioka, Teruyuki
2017.
Club-Isomorphisms of Aronszajn Trees in the Extension with a Suslin Tree.
Notre Dame Journal of Formal Logic,
Vol. 58,
Issue. 3,
Brodsky, Ari Meir
and
Rinot, Assaf
2017.
A microscopic approach to Souslin-tree constructions, Part I.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 11,
p.
1949.
Habič, Miha E.
2017.
The grounded Martin's axiom.
Mathematical Logic Quarterly,
Vol. 63,
Issue. 5,
p.
437.
Tall, Franklin D.
2017.
PFA(S)[S] for the masses.
Topology and its Applications,
Vol. 232,
Issue. ,
p.
13.
Dow, Alan
and
Tall, Franklin D.
2017.
PFA(S)[S] and countably compact spaces.
Topology and its Applications,
Vol. 230,
Issue. ,
p.
393.
Dow, Alan
and
Tall, Franklin D.
2018.
Normality Versus Paracompactness in Locally Compact Spaces.
Canadian Journal of Mathematics,
Vol. 70,
Issue. 1,
p.
74.
Dow, Alan
2019.
PFA(S) and countable tightness.
Topology and its Applications,
Vol. 256,
Issue. ,
p.
60.
Dow, Alan
and
Tall, Franklin
2019.
Hereditarily normal manifolds of dimension greater than one may all be metrizable.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 10,
p.
6805.
Krueger, John
2020.
A forcing axiom for a non-special Aronszajn tree.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 8,
p.
102820.
Brodsky, Ari Meir
and
Rinot, Assaf
2021.
A microscopic approach to Souslin-tree construction, Part II.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 5,
p.
102904.

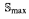 variation for one souslin tree
variation for one souslin tree