Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T08:25:20.704Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic and coanalytic families of almost disjoint functions

Published online by Cambridge University Press:  12 March 2014

Bart Kastermans ,
Juris Steprāns  and
Yi Zhang
Bart Kastermans
Affiliation:
Department of Mathematics, University of Wisconsin, 480 Lincoln Dr, Madison, Wi 53706-1388, USA, E-mail: kasterma@math.wisc.edu Institute of Logic and Cognition, Sun Yat-Sen University, Guangzhou, 510275, P.R.China
Juris Steprāns
Affiliation:
Department of Mathematics, York University, 4700 Keele Street, Toronto, Ontario. M3J 1P3, Canada, E-mail: steprans@yorku.ca Institute of Logic and Cognition, Sun Yat-Sen University, Guangzhou, 510275, P.R.China
Yi Zhang
Affiliation:
Institute of Logic and Cognition, Sun Yat-Sen University, Guangzhou, 510275, P.R.China Department of Mathematics, Sun Yat-Sen University, Guangzhou, 510275, P.R.China, E-mail: yizhang@umich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

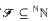If is an analytic family of pairwise eventually different functions then the following strong maximality condition fails: For any countable 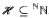, no member of which is covered by finitely many functions from 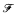, there is 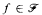such that for all 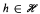there are infinitely many integers k such that f(k) = h(k). However if V = L then there exists a coanalytic family of pairwise eventually different functions satisfying this strong maximality condition.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 4 , December 2008 , pp. 1158 - 1172
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Brendle, J., Just, W., and Laflamme, C., On the refinement and countable refinement numbers, Questions and Answers in General Topology, vol. 18 (2000), pp. 123–128.Google Scholar
[2]Devlin, K. J., Constructibility, Springer-Verlag, 1984.CrossRefGoogle Scholar
[3]Hinman, P. G., Recursion-theoretic hierarchies, Springer-Verlag, 1978.CrossRefGoogle Scholar
[4]Kamburelis, A. and Wȩolorz, B.. Splittings, Archive for Mathematical Logic, vol. 35 (1996), pp. 263–277.CrossRefGoogle Scholar
[5]Kechris, A. S., Classical descriptive set theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.CrossRefGoogle Scholar
[6]Kunen, K., Set theory. An introduction to independence proofs, North-Holland, 1980.Google Scholar
[7]Mathias, A. R. D., Happy families, Annals of Mathematical Logic, vol. 12 (1977), no. 1, pp. 59–111.CrossRefGoogle Scholar
[8]Mathias, A. R. D., Weak systems of Gandy, Jensen and Devlin. Set theory. Trends in Mathematics, Birkhäuser, 2006, pp. 149–224.CrossRefGoogle Scholar
[9]Miller, A. W., Infinite combinatorics and definability, Annals of Pure and Applied Logic, vol. 41 (1989), pp. 179–203.CrossRefGoogle Scholar
[10]Solecki, S.Analytic ideals and their applications. Annals of Pure and Applied Logic, vol. 99 (1999), pp. 51–72.CrossRefGoogle Scholar
[11]Talagrand, M., Compacts defonctions mesurables etfiltres non mesurables, Studia Mathematica, vol. 67 (1980), no. 1, pp. 13–43.CrossRefGoogle Scholar
[12]Todorčevic, S., Analytic gaps, Fundamenta Mathematicae, vol. 150 (1996), pp. 55–66.CrossRefGoogle Scholar