Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T06:57:00.414Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic cell decomposition and the closure of p-adic semianalytic sets

Published online by Cambridge University Press:  12 March 2014

Nianzheng Liu
Nianzheng Liu*
Affiliation:
International Business Machines Corporation, 6300 Diagonal Hwy., 004/004A, Boulder, CO 80301, USA. E-mail: liun@vnet.ibm.com
Get access Rights & Permissions [Opens in a new window]

Extract

The p-adic semianalytic sets are defined, locally, as boolean combinations of sets of the form 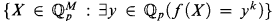over the p-adic fields ℚp, where f is an analytic function. A well-know example due to Osgood showed the projection of a semianalytic set need not be a semianalytic set. We call those sets that are, locally, the projections of p-adic semianalytic sets p-adic subanalytic sets. The theory of p-adic subanalytic sets was presented by Denef and Van den Dries in [5]. The basic tools are the quantifier elimination techniques together with the ultrametric Weierstrass Preparation Theorem. Simultaneously with their developments of the p-adic subanalytic sets, they established some basic properties of p-adic semianalytic sets.

In this paper, we prove that the closure of any p-adic semianalytic set is also a semianalytic set. The analogous property for real semianalytic sets was proved in [12] and that for rigid semianalytic sets, informed by the referee, has been proved recently by a quite different method in [14] (cf. [9]). The keys to the proof are a separation lemma (Lemma 2) and an analytic cell decomposition theorem (Theorem 2) which is an analytic version of Denef's cell decomposition theorem (see [3, 4]; A total different form of anayltic cells appeared in [13]). The analytic cell decomposition theorem allows us to partition certain kinds of basic subsets into analytic cells that possess the closure property (see §1 for the definition).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 1 , March 1997 , pp. 285 - 303
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bosch, S., Güntzer, U., and Remmert, R., Non-archimedean analysis, Springer-Verlag, 1984.CrossRefGoogle Scholar
[2]Cohen, P. J., Decision procedures for real and p-adic fields, Communications on Pure and Applied Mathematics, vol. 22 (1969), pp. 131–151.CrossRefGoogle Scholar
[3]Denef, J., The rationality of the Poincare' series associated to the p-adic points on a variety, Inventiones Mathematicae, vol. 77 (1984), pp. 1–23.CrossRefGoogle Scholar
[4]Denef, J., p-adic semi-algebraic sets and cell decomposition, J. für reine und Angew. Math, vol. 369 (1986), pp. 154–166.Google Scholar
[5]Denef, J. and van den Dries, L., p-adic and real subanalytic sets, Annuals of Mathematics, vol. 128 (1988), pp. 79–138.CrossRefGoogle Scholar
[6]Koblitz, N., p-adic numbers, p-adic analysis and Zeta functions, second GTM 58 ed., 1984.CrossRefGoogle Scholar
[7]Lipshitz, L., Isolated points on fibers of affinoid varieties, Journal für Reine und Angewandte Mathematik, vol. 384 (1988), pp. 208–220.Google Scholar
[8]Lipshitz, L., p-adic zeros of polynomials, Journal für Reine und Angewandte Mathematik, vol. 390 (1988), pp. 208–214.Google Scholar
[9]Lipshitz, L., Rigid subanalytic sets, American Journal of Mathematics, vol. 115 (1993), pp. 77–108.CrossRefGoogle Scholar
[10]Liu, N., Geometric theory of valued fields, Ph.D. thesis, Purdue University, 1994.Google Scholar
[11]Macintyre, A., On definable subsets of p-adic fields, this Journal, vol. 41 (1976), pp. 605–610.Google Scholar
[12]Łojasiewicz, S., Ensembles sémi-analytiques, IHES, Burres-sur-Yvette, 1965.Google Scholar
[13]Pas, J., Uniform p-adic cell decomposition and local zeta functions, Journal für Reine und Angewandte Mathematik, vol. 399 (1991), pp. 137–172.Google Scholar
[14]Schoutens, H., Closure of rigid semianalytic sets, preprint, 1995.Google Scholar
[15]Scowcroft, P. and van den Dries, L., On the structure of semialgebraic sets over p-adic fields, this Journal, vol. 53 (1988), pp. 1138–1164.Google Scholar
[16]Serre, J.-P., Lie algebras and Lie groups, Mathematics Lecture Notes, Benjamin, 1964.Google Scholar