Another variant of natural deduction

Extract

Since 1934 various different techniques for natural deduction have been developed by Gentzen, Jaśkowski, Rosser, Quine, and others (see [1], pp. 147–167; [2], especially footnotes 1, 3, and 4; and [3], pp. 75-83, 96-107, and 289-294). It has been pointed out to me by Professor Donald Kalish of U.C.L.A. that the restrictions placed upon Universal Generalization (UG) and Existential Instantiation (EI) in [3] force one to construct a less natural proof than seems desirable for such arguments as

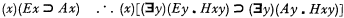
(cf. [3], p. 139, and [1], pp. 175f.) It is my purpose in this note to formulate an alternative restriction on UG which will permit a more natural proof for such arguments, and to prove the consistency of the altered rule.

In the notation of [3], “The expression ‘Φμ’ will denote any propositional function in which there is at least one free occurrence of the variable denoted by ‘μ’. The expression ‘Φν’ will denote the result of replacing all free occurrences of μ in Φμ by ν, with the added proviso that when ν is a variable it must occur free in Φν at all places at which μ occurs free in Φμ.” ([3], p. 100.) The statement of EI is relatively unrestricted; being

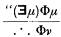
provided that ν is a variable which occurs free in no earlier step.” ([3], p. 104.)