Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T19:12:15.965Z Has data issue: false hasContentIssue false
  • English
  • Français

Applications of vaught sentences and the covering theorem1

Published online by Cambridge University Press:  12 March 2014

Victor Harnik  and
Michael Makkai
Victor Harnik
Affiliation:
Dartmouth College, Hanover, New Hampshire 03755
Michael Makkai
Affiliation:
Université de Montréal, Montréal, Québec, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

We use a fundamental theorem of Vaught, called the covering theorem in [V] (cf. theorem 0.1 below) as well as a generalization of it (cf. Theorem 0.1* below) to derive several known and a few new results related to the logic 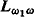. Among others, we prove that if every countable model in a PCφ1ω class has only countably many automorphisms, then the class has either ≤ℵ0 or exactly 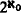nonisomorphic countable members (cf. Theorem 4.3*) and that the class of countable saturated structures of a sufficiently large countable similarity type is not 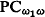among countable structures (cf. Theorem 5.2). We also give a simple proof of the Lachlan-Sacks theorem on bounds of Morley ranks (§7).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 1 , March 1976 , pp. 171 - 187
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The authors' work was supported by a grant of the National Research Council of Canada.

References

REFERENCES

[B] Barwise, Jon, Back and forth through infinitary logic, Studies in model theory, Studies in Mathematics, Vol. 8 (Morley, M. D., Editor), The Mathematical Association of America, 1973.Google Scholar
[C] Chano, C. C., Some new results in definability, Bulletin of the American Mathematical Society, vol. 70 (1964), pp. 808–813.CrossRefGoogle Scholar
[G] Garland, S. J., Generalized interpolation theorems, this Journal, vol. 37 (1972), pp. 343–351.Google Scholar
[Ke] Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[H] Harnik, V., On the existence of saturated models of stable theories, Proceedings of the American Mathematical Society, (to appear).Google Scholar
[Ku] Kueker, D. W., Definability, automorphisms and infinitary languages, Lecture Notes in Mathematics, vol. 72, Springer-Verlag, Berlin, 1968, pp. 152–165.Google Scholar
[La] Lachlan, A. H., The transcendental rank of a theory, Pacific Journal of Mathematics, vol. 37 (1971), pp. 119–122.CrossRefGoogle Scholar
[Li] Lindström, P., On relations between structures, Theoria (Lund), (1966), pp. 172–185.Google Scholar
[Ma 1] Makkai, M., On a generalization of a theorem of E. W. Beth, Acta Mathematica Academiae Scientarium Hungaricae, vol. 15 (1964), pp. 227–235.CrossRefGoogle Scholar
[Ma 2] Makkai, M., Svenonius sentences and Lindström's theory on preservation theorems, Fundamenta Mathematicae, vol. 73 (1972), pp. 219–233.CrossRefGoogle Scholar
[Ma 3] Makkai, M., Vaught sentences and Lindström's regular relations, Lecture Notes in Mathemattes, no. 337, Cambridge Summer School in Mathematical Logic, Springer, Berlin, 1973, pp. 622–660.Google Scholar
[Ma 4] Makkai, M., Global definability theory in Lω1ω , Bulletin of the American Mathematical Society, vol. 79 (1973), pp. 916–921.CrossRefGoogle Scholar
[Ma 5] Makkai, M., An “admissible” generalization of a theorem on countable Σ1 ′ sets with applicalions (to appear).Google Scholar
[Man] Mansfield, R., Perfect subsets of definable sets of real numbers, Pacific Journal of Mathematics, vol. 35 (1970), pp. 451–457.CrossRefGoogle Scholar
[Mor 1] Morley, M., Categoricity in power, Transactions of the American Mathematical Society, vol. 114 (1965), pp. 514–538.CrossRefGoogle Scholar
[Mor 2] Morley, M., The number of countable models, this Journal, vol. 35 (1970), pp. 14–18.Google Scholar
[Mot] Motohashi, N., A new theorem on definability, preprint; also, Dissertation, University of Tokyo, 1971.Google Scholar
[R] Reyes, G. E., Local definability theory, Annals of Mathematical Logic, vol. 1 (1970), pp. 95–137.CrossRefGoogle Scholar
[Sa 1] Sacks, G. E., Saturated model theory, Benjamin, Reading, Massachusetts, 1972.Google Scholar
[Sa 2] Sacks, G. E., Effective bounds on Morley rank (to appear).Google Scholar
[Sa 3] Sacks, G. E., On the number of countable models (to appear).Google Scholar
[Sh 1] Shelah, S., Uniqueness and characterization of prime models over sets for totally transcendental first-order theories, this Journal, vol. 37 (1972), pp. 107–113.Google Scholar
[Sh 2] Shelah, S., Categoricity of uncountable theories, Proceedings of Symposia in Pure Mathematics, vol. 25 (Tarski Symposium, Berkeley, 1971), American Mathematical Society, Providence, R.I., 1974, pp. 187–204.Google Scholar
[Sh 3] Shelah, S., Stability, the f.c.p. and superstability; model theoretic properties of formulas in first order theory, Annals of Mathematical Logic, vol. 3 (1971), pp. 271–362.CrossRefGoogle Scholar
[Sv 1] Svenonius, L., A theorem on permutations in models, Theoria (Lund), vol. 25 (1959), pp. 173–178.CrossRefGoogle Scholar
[Sv 2] Shelah, S., On the denumerable models of theories with extra predicates, The theory of models, North-Holland, Amsterdam, 1965, pp. 376–389.Google Scholar
[V] Vauoht, R., Descriptive set theory in Lω1ω , Lecture Notes in Mathematics, no. 337, Cambridge Summer School in Mathematical Logic, Springer, Berlin, 1973, pp. 574–598.Google Scholar