Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T19:30:51.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximate Euler characteristic, dimension, and weak pigeonhole principles

Published online by Cambridge University Press:  12 March 2014

Jan Krajíček
Jan Krajíček*
Affiliation:
Mathematical Institute, Academy of Sciences, Žitná 25, Prague 1, CZ-115 67, The Czech Republic, E-mail: krajicek@math.cas.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

We define the notion of approximate Euler characteristic of definable sets of a first order structure. We show that a structure admits a non-trivial approximate Euler characteristic if it satisfies weak pigeonhole principle 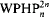: two disjoint copies of a non-empty definable set A cannot be definably embedded into A, and principle CC of comparing cardinalities: for any two definable sets A, B either A definably embeds in B or vice versa. Also, a structure admitting a non-trivial approximate Euler characteristic must satisfy .

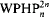Further we show that a structure admits a non-trivial dimension function on definable sets if and only if it satisfies weak pigeonhole principle : for no definable set A with more than one element can A2 definably embed into A.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 201 - 214
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ajtai, M., On the existence of modulo p cardinality functions, Feasible mathematics II (Clote, P. and Remmel, J., editors), Birkhäuser, 1994, pp. 1–14.Google Scholar
[2]Ax, J., The elementary theory of finite fields, Annals of Mathematics, vol. 88 (1968), no. 2, pp. 239–271.Google Scholar
[3]Chatzidakis, Z., van den Dries, L., and Macintyre, A., Definable sets over finite fields, Journal für die reine und angewandte Mathematik, vol. 427 (1992), pp. 107–135.Google Scholar
[4]Krajíček, J., Bounded arithmetic, propositional logic, and complexity theory, Encyclopedia of Mathematics and Its Applications, vol. 60, Cambridge University Press, 1995.Google Scholar
[5]Krajíček, J., Uniform families of polynomial equations over a finite field and structures admitting an Euler characteristic of definable sets, Proceedings of the London Mathematical Society, vol. 81 (2000), no. 3, pp. 257–284.CrossRefGoogle Scholar
[6]Krajíček, J., Combinatorics of first order structures and propositional proof systems, Archive for Mathematical Logic, (to appear, preprint 2001).Google Scholar
[7]Krajíček, J., Pudlák, P., and Woods, A., Exponential lower bound to the size of bounded depth Frege proofs of the pigeonhole principle, Random Structures and Algorithms, vol. 7 (1995), no. 1, pp. 15–39.Google Scholar
[8]Krajíček, J. and Scanlon, T., Combinatorics with definable sets: Euler characteristics and Grothendieck rings, The Bulletin of Symbolic Logic, vol. 6 (2001), no. 3, pp. 311–330.Google Scholar
[9]Paris, J. B., Wilkie, A. J., and Woods, A. R., Provability of the pigeonhole principle and the existence of infinitely many primes, this Journal, vol. 53 (1988), pp. 1235–1244.Google Scholar
[10]Pitassi, T., Beame, P., and Impagliazzo, R., Exponential lower bounds for the pigeonhole principle, Computational complexity, vol. 3 (1993), pp. 97–308.CrossRefGoogle Scholar
[11]Schanuel, S., Negative sets have Euler characteristic and dimension, Category theory: Como '90 (Carboni, A, Pedicchio, M., and Rosolini, G., editors), Lecture Notes in Mathematics, vol. 1488, Springer-Verlag, 1991, pp. 379–385.Google Scholar
[12]van den Dries, L., Tame topology and o-minimal structures, London Mathematical Society Lecture Note Series, vol. 248, Cambridge University Press, 1998.CrossRefGoogle Scholar