Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T10:11:30.216Z Has data issue: false hasContentIssue false
  • English
  • Français

ARONSZAJN TREE PRESERVATION AND BOUNDED FORCING AXIOMS

Part of: Set theory

Published online by Cambridge University Press:  01 February 2021

GUNTER FUCHS
GUNTER FUCHS*
Affiliation:
DEPARTMENT OF MATHEMATICS, THE GRADUATE CENTER THE CITY UNIVERSITY OF NEW YORK 365 FIFTH AVENUE, NEW YORK, NY10016, USA DEPARTMENT OF MATHEMATICS, COLLEGE OF STATEN ISLAND THE CITY UNIVERSITY OF NEW YORK STATEN ISLAND, NEW YORK, NY10314, USAE-mail: gunter.fuchs@csi.cuny.eduURL: http://www.math.csi.cuny/edu/~fuchs
Get access Rights & Permissions [Opens in a new window]

Abstract

I investigate the relationships between three hierarchies of reflection principles for a forcing class 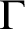$\Gamma $ : the hierarchy of bounded forcing axioms, of 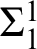$\Sigma ^1_1$ -absoluteness, and of Aronszajn tree preservation principles. The latter principle at level 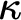$\kappa $ says that whenever T is a tree of height 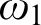$\omega _1$ and width 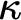$\kappa $ that does not have a branch of order type 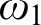$\omega _1$ , and whenever 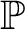${\mathord {\mathbb P}}$ is a forcing notion in 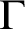$\Gamma $ , then it is not the case that 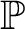${\mathord {\mathbb P}}$ forces that T has such a branch. 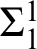$\Sigma ^1_1$ -absoluteness serves as an intermediary between these principles and the bounded forcing axioms. A special case of the main result is that for forcing classes that don’t add reals, the three principles at level 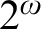$2^\omega $ are equivalent. Special attention is paid to certain subclasses of subcomplete forcing, since these are natural forcing classes that don’t add reals.

Keywords

subcomplete forcingforcing axiomsgeneric absolutenessAronszajn treescontinuum hypothesis

MSC classification

Primary: 03E50: Continuum hypothesis and Martin's axiom
Secondary: 03E57: Generic absoluteness and forcing axioms 03E35: Consistency and independence results 03E55: Large cardinals 03E05: Other combinatorial set theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 1 , March 2021 , pp. 293 - 315
Check for updates
Copyright
© The Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagaria, J., Gitman, V., and Schindler, R., Remarkable cardinals, structural reflection, and the weak proper forcing axiom . Archive for Mathematical Logic , vol. 56 (2017), no. 1, pp. 1–20.CrossRefGoogle Scholar
Claverie, B. and Schindler, R., Woodin’s axiom (*), bounded forcing axioms, and precipitous ideals on ω1 , this Journal, vol. 77 (2012), no. 2, pp. 475–498.Google Scholar
Foreman, M., Magidor, M., and Shelah, S., Martin’s maximum, saturated ideals, and non-regular ultrafilters. Part I . Annals of Mathematics , vol. 127 (1988), no. 1, pp. 1–47.CrossRefGoogle Scholar
Fuchs, G., Closure properties of parametric subcompleteness . Archive for Mathematical Logic , vol. 57 (2018), no. 7–8, pp. 829–852.CrossRefGoogle Scholar
Fuchs, G., Hierarchies of forcing axioms, the continuum hypothesis and square principles , this Journal, vol. 83 (2018), no. 1, pp. 256–282.Google Scholar
Fuchs, G., Subcomplete forcing principles and definable well-orders . Mathematical Logic Quarterly , vol. 64 (2018), no. 6, pp. 487–504.CrossRefGoogle Scholar
Fuchs, G., Diagonal reflections on squares . Archive for Mathematical Logic , vol. 58 (2019), no. 1, pp. 1–26.CrossRefGoogle Scholar
Fuchs, G., Canonical fragments of the strong reflection principle. Journal of Mathematical Logic, accepted. arXiv:2009.06065 [math.LO].Google Scholar
Fuchs, G. and Lambie-Hanson, C., Separating diagonal stationary reflection principles, this Journal, vol. 86 (2021), no. 1, pp. 262–292.Google Scholar
Fuchs, G. and Minden, K., Subcomplete forcing, trees and generic absoluteness , this Journal, vol. 83 (2018), no. 3, pp. 1282–1305.Google Scholar
Goldstern, M. and Shelah, S., The bounded proper forcing axiom , this Journal, vol. 60 (1995), no. 1, pp. 58–73.Google Scholar
Jech, T., Set Theory , Springer Monographs in Mathematics, Springer, Berlin and Heidelberg, 2003.Google Scholar
Jensen, R. B., The fine structure of the constructible hierarchy . Annals of Mathematical Logic , vol. 4 (1972), pp. 229–308.CrossRefGoogle Scholar
Jensen, R. B., Subcomplete forcing and $\mathbf{\mathcal{L}}$ -forcing, E-Recursion, Forcing and C ${\vphantom{0}}^{*}$ -Algebras (Chong, C., Feng, Q., Slaman, T. A., Woodin, W. H., and Yang, Y., editors), Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 27, World Scientific, Singapore, 2014, pp. 83–182.CrossRefGoogle Scholar
Jensen, R. B., Subproper and subcomplete forcing, handwritten notes, 2009. Available at https://www.mathematik.hu-berlin.de/˜raesch/org/jensen.html.Google Scholar
Jensen, R. B., Iteration theorems for subcomplete and related forcings, handwritten notes, 2014–15. Available at https://www.mathematik.hu-berlin.de/˜raesch/org/jensen.html.CrossRefGoogle Scholar
Jensen, R. B., On the subcompleteness of some Namba-type forcings, handwritten notes, 2017. Available at https://www.mathematik.hu-berlin.de/˜raesch/org/jensen.html.Google Scholar
Larson, P., Separating stationary reflection principles , this Journal, vol. 65 (2000), no. 1, pp. 247–258.Google Scholar
Mildenberger, H. and Shelah, S., Specialising Aronszajn trees and preserving some weak diamonds . Journal of Applied Analysis , vol. 15 (2009), no. 1, pp. 47–78.CrossRefGoogle Scholar
Minden, K., On subcomplete forcing , Ph.D. thesis, The CUNY Graduate Center, 2017.Google Scholar
Miyamoto, T., A note on weak segments of PFA , Proceedings of the Sixth Asian Logic Conference (Chong, C. T., Feng, Q., Ding, D., Huang, Q., and Yasugi, M., editors), World Scientific Publishing, Singapore, 1998, pp. 175–197.CrossRefGoogle Scholar
Schimmerling, E., Coherent sequences and threads . Advances in Mathematics , vol. 216 (2007), pp. 89–117.CrossRefGoogle Scholar
Villaveces, A., Chains of end elementary extensions of models of set theory , this Journal, vol. 63 (1998), no. 3, pp. 1116–1136.Google Scholar
Zapletal, J., Bounded Namba forcing axiom may fail . Mathematical Logic Quarterly , vol. 64 (2018), no. 3, pp. 170–172.CrossRefGoogle Scholar