Article contents
BASES AND BOREL SELECTORS FOR TALL FAMILIES
Published online by Cambridge University Press: 30 January 2019
Abstract
Given a family  ${\cal C}$ of infinite subsets of
${\cal C}$ of infinite subsets of  ${\Bbb N}$, we study when there is a Borel function
${\Bbb N}$, we study when there is a Borel function 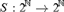 $S:2^{\Bbb N}\to 2^{\Bbb N} $ such that for every infinite
$S:2^{\Bbb N}\to 2^{\Bbb N} $ such that for every infinite 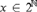 $x \in 2^{\Bbb N} $,
$x \in 2^{\Bbb N} $, 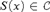 $S\left( x \right) \in {\Cal C}$ and
$S\left( x \right) \in {\Cal C}$ and 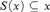 $S\left( x \right) \subseteq x$. We show that the family of homogeneous sets (with respect to a partition of a front) as given by the Nash-Williams’ theorem admits such a Borel selector. However, we also show that the analogous result for Galvin’s lemma is not true by proving that there is an
$S\left( x \right) \subseteq x$. We show that the family of homogeneous sets (with respect to a partition of a front) as given by the Nash-Williams’ theorem admits such a Borel selector. However, we also show that the analogous result for Galvin’s lemma is not true by proving that there is an 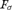 $F_\sigma$ tall ideal on
$F_\sigma$ tall ideal on  ${\Bbb N}$ without a Borel selector. The proof is not constructive since it is based on complexity considerations. We construct a
${\Bbb N}$ without a Borel selector. The proof is not constructive since it is based on complexity considerations. We construct a 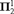 ${\bf{\Pi }}_2^1 $ tall ideal on
${\bf{\Pi }}_2^1 $ tall ideal on  ${\Bbb N}$ without a tall closed subset.
${\Bbb N}$ without a tall closed subset.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 3
- Cited by

