Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T17:38:00.725Z Has data issue: false hasContentIssue false
  • English
  • Français

Beth's property fails in L<ω1

Published online by Cambridge University Press:  12 March 2014

Lee Badger
Lee Badger*
Affiliation:
Middlebury College, Middlebury, Vermont 05753
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we prove that Beth's property does not hold in L<ω. This answers a question posed by Magidor and Malitz in [8]. Beth's property is a natural closure condition on a language which says that everything implicitly definable in the language is also explicitly definable in the language. That the first-order predicate calculus (L0) has the property was first shown by Beth [4]. Lopez-Escobar proved that 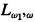also has Beth's property [7]. Malitz [9] showed the Beth's property fails in Lκλ where κ ≥ λ ≥ ω1. Friedman and Silver showed that the property fails in Lκλ for κ > ω1. Also Friedman [5] showed that extensions of elementary logic using cardinality quantifiers (L)1κ do not have Beth's property.

The undefined notation used here is standard. If further clarification is needed, we refer the reader to [3]. κ and λ denote infinite cardinals. cX and ȣX∣ denote the cardinality of X. cfμ will denote the cofinality of the order μ. All languages discussed are assumed to have no function or constant symbols. All structures are relational. The type of a formula is the set of relation symbols appearing in the formula (excluding equality). The type of a set of formulas is the set of all relation symbols appearing in some formula of the set of formulas. For purpose of this paper we will assume that to each n-ary relation in a structure there is associated an n-ary relation symbol and that in any given structure this association is one-to-one. Using this convention we can define the type of a structure to be the set of those relation symbols to which there is associated a relation in the structure. Sometimes we use the term predicate instead of relation.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 45 , Issue 2 , June 1980 , pp. 284 - 290
Copyright
Copyright © Association for Symbolic Logic 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This material appeared in the author's doctoral dissertation, University of Colorado, 1975.

References

REFERENCES

[1]Badger, L., Beth's theorem fails in L<ω, Notices of the American Mathematical Society, vol. 21 (1974), p. A–322, Abstract 74T-E32.Google Scholar
[2]Badger, L., The Malitz quantifier meets its Ehrenfeucht game, Ph.D. Thesis, University of Colorado, 1975.Google Scholar
[3]Badger, L., An Ehrenfeucht game for the multivariable quantifiers of Malitz and some applications, Pacific Journal of Mathematics, vol. 72 (1977), pp. 293–304.CrossRefGoogle Scholar
[4]Beth, E., On Padoa's method in the theory of definition, Indagationes Mathematicae, vol. 15 (1953), pp. 330–339.CrossRefGoogle Scholar
[5]Friedman, H., Beth's theorem in cardinality logics, Israel Journal of Mathematics, vol. 14 (1973), pp. 205–212.CrossRefGoogle Scholar
[6]Lindström, P., On extensions of elementary logic, Theoria, vol. 35 (1969), pp. 1–11.CrossRefGoogle Scholar
[7]Lopez-Escobar, E., An interpolation theorem for denumerably long formulas, Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
[8]Magidor, M. and Malitz, J., Compact extensions of L(Q). (Part 1a), Annals of Mathematical Logic, vol. 11 (1977), pp. 217–261.CrossRefGoogle Scholar
[9]Malitz, J., Infinitary analogs of theorems from first order model theory, this Journal, vol. 36 (1971), pp. 216–228.Google Scholar
[10]Magidor, M., Makowsky, J. and Stavi, J., Unpublished result that Craig's theorem fails in L <ω.Google Scholar
[11]Yasuhara, M., An axiomatic system for the first-order language with an equi-cardinality quantifier, this Journal, vol. 31 (1966), pp. 635–640.Google Scholar