No CrossRef data available.
Article contents
THE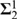 
${\bf{\Sigma }}_2^1$ COUNTERPARTS TO STATEMENTS THAT ARE EQUIVALENT TO THE CONTINUUM HYPOTHESIS
Published online by Cambridge University Press: 22 December 2015
Abstract
We consider natural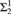 
${\rm{\Sigma }}_2^1$ definable analogues of many of the classical statements that have been shown to be equivalent to CH. It is shown that these 
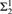${\rm{\Sigma }}_2^1$ analogues are equivalent to that all reals are constructible. We also prove two partition relations for 
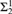${\rm{\Sigma }}_2^1$ colourings which hold precisely when there is a non-constructible real.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2015
References
REFERENCES
Banach, Stefan, Sur les transformations biunivoques. Fundamenta Mathematicae, vol. 19 (1932), pp.10–16.CrossRefGoogle Scholar
Jech, Thomas, Set theory, The third millennium edition, revised and expanded, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Kanamori, Akihiro, The higher infinite:Large cardinals in set theory from their beginnings, second ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Kechris, Alexander S., Measure and category in effective descriptive set theory. Annals of Mathematical Logic, vol. 5 (1972/73), pp. 337–384.CrossRefGoogle Scholar
Kechris, Alexander S., Classical descriptive set theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.CrossRefGoogle Scholar
Komjáth, Péter, Three clouds may cover the plane. Annals of Pure and Applied Logic, vol. 109 (2001), no. 1–2, pp. 71–75.CrossRefGoogle Scholar
Komjáth, Péter and Totik, Vilmos, Problems and theorems in classical set theory, Problem Books in Mathematics, Springer, New York, 2006.Google Scholar
Mansfield, Richard, Perfect subsets of definable sets of real numbers. Pacific Journal of Mathematics, vol. 35 (1970), pp. 451–457.CrossRefGoogle Scholar
Mansfield, Richard and Weitkamp, Galen, Recursive aspects of descriptive set theory, Oxford Logic Guides, vol. 11, The Clarendon Press Oxford University Press, New York, 1985.Google Scholar
Miller, Arnold W., Infinite combinatorics and definability. Annals of Pure and Applied Logic, vol. 41 (1989), no. 2, pp. 179–203.CrossRefGoogle Scholar
Morayne, M., On differentiability of Peano type functions. Colloquium Mathematicum, vol. 48 (1984), no. 2, pp. 261–264. MR 758535 (86i:26008)CrossRefGoogle Scholar
Moschovakis, Yiannis N., Descriptive set theory, second ed., Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.Google Scholar
Shoenfield, J. R., The problem of predicativity, Essays on the foundations of mathematics, Magnes Press, Hebrew University, Jerusalem, 1961, pp. 132–139.Google Scholar
Sierpiński, Wacław, Cardinal and ordinal numbers, Second revised edition, Monografie Matematyczne, vol. 34, Państowe Wydawnictwo Naukowe, Warsaw, 1965.Google Scholar
Solovay, Robert M., On the cardinality of 
$\mathop \sum \nolimits^ _2^1$sets of reals, Foundations of Mathematics (Symposium Commemorating Kurt Gödel, Columbus, Ohio, 1966), Springer, New York, 1969, pp. 58–73.Google Scholar
$\mathop \sum \nolimits^ _2^1$sets of reals, Foundations of Mathematics (Symposium Commemorating Kurt Gödel, Columbus, Ohio, 1966), Springer, New York, 1969, pp. 58–73.Google ScholarSteel, John R., An outline of inner model theory, Handbook of set theory, Springer, Dordrecht, 2010, pp. 1595–1684.CrossRefGoogle Scholar
Törnquist, Asger and Weiss, William, Definable Davies’ theorem. Fundamenta Mathematicae, vol. 205 (2009), no. 1, pp. 77–89.CrossRefGoogle Scholar
Trzeciakiewicz, Leon, Remarque sur les translations des ensembles linéaires. Comptes Rendus des Séances de la Société des Sciences et des Lettres de Varsovie, vol. 25 (1933), pp. 63–65 (French).Google Scholar