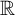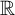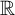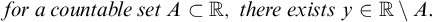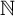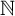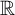BIG IN REVERSE MATHEMATICS: THE UNCOUNTABILITY OF THE REALS

Abstract

The uncountability of $\mathbb {R}$ is one of its most basic properties, known far outside of mathematics. Cantor’s 1874 proof of the uncountability of $\mathbb {R}$ even appears in the very first paper on set theory, i.e., a historical milestone. In this paper, we study the uncountability of ${\mathbb R}$ in Kohlenbach’s higher-order Reverse Mathematics (RM for short), in the guise of the following principle:

$$\begin{align*}\mathit{for \ a \ countable \ set } \ A\subset \mathbb{R}, \mathit{\ there \ exists } \ y\in \mathbb{R}\setminus A. \end{align*}$$

An important conceptual observation is that the usual definition of countable set—based on injections or bijections to ${\mathbb N}$—does not seem suitable for the RM-study of mainstream mathematics; we also propose a suitable (equivalent over strong systems) alternative definition of countable set, namely union over ${\mathbb N}$ of finite sets; the latter is known from the literature and closer to how countable sets occur ‘in the wild’. We identify a considerable number of theorems that are equivalent to the centred theorem based on our alternative definition. Perhaps surprisingly, our equivalent theorems involve most basic properties of the Riemann integral, regulated or bounded variation functions, Blumberg’s theorem, and Volterra’s early work circa 1881. Our equivalences are also robust, promoting the uncountability of ${\mathbb R}$ to the status of ‘big’ system in RM.

1 Introduction

1.1 Summary

Like Hilbert [34], we believe the infinite to be a central object of study in mathematics. That the infinite comes in ‘different sizes’ is a relatively new insight, due to Cantor around 1874 [19], in the guise of the uncountability of ${\mathbb R}$ , also known simply as Cantor’s theorem. We have previously studied the uncountability of ${\mathbb R}$ in the guise of the following third-order ¹ principles.

• • $\mathsf {NIN}$ : there is no injection from $[0,1]$ to ${\mathbb N}$ .

• • $\mathsf {NBI}$ : there is no bijection from $[0,1]$ to ${\mathbb N}$ .

In particular, as shown in [69–71], the principles $\mathsf {NBI}$ and $\mathsf {NIN}$ are hard to prove in terms of conventional ² comprehension, while the objects claimed to exist are hard to compute in terms of the other data, in the sense of Kleene’s computability theory based on S1–S9 [46, 58]. As shown in [79], this hardness remains if we restrict the mappings in $\mathsf {NIN}$ and $\mathsf {NBI}$ to well-known function classes, e.g., based on bounded variation, Borel, upper semi-continuity, and quasi-continuity. Moreover, many basic third-order theorems imply $\mathsf {NIN}$ or $\mathsf {NBI}$ , and the same at the computational level (see [68–71, 77–80]). Finally, $\mathsf {NIN}$ and $\mathsf {NBI}$ seem to be the weakest natural third-order principles that boast all the aforementioned properties.

For all these reasons, the study of the uncountability of ${\mathbb R}$ in Reverse Mathematics (RM for short; see Section 1.3.1) seems like a natural enterprise. However, try as we might we have not managed to obtain elegant equivalences for $\mathsf {NIN}$ and $\mathsf {NBI}$ , working in Kohlenbach’s higher-order Reverse Mathematics (see Section 1.3.1).

As argued in detail in Section 2, our main problem is that countable sets that occur ‘in the wild’ do not have injections (let alone bijections) to ${\mathbb N}$ that can be defined in weak logical systems. By contrast, the (equivalent over $\mathsf {ZF}$ and weaker systems) definition of countable set as in Definitions 1.1 and 1.2 is much more suitable for the development of higher-order RM and is central to this paper.

Definition 1.1. A set $A\subset {\mathbb R}$ is height countable if there is a height function $H:{\mathbb R}\rightarrow {\mathbb N}$ for A, i.e., for all $n\in {\mathbb N}$ , $A_{n}:= \{ x\in A: H(x)<n\}$ is finite.

Definition 1.2 (Finite set)

Any $X\subset {\mathbb R}$ is finite if there is $N\in {\mathbb N}$ such that for any finite sequence $(x_{0}, \dots , x_{N})$ of distinct reals, there is $i\leq N$ such that $x_{i}\not \in X$ .

The notion of ‘height function’ can be found in the literature in connection to countability [40, 49, 59, 75, 97], while ‘height countable’ essentially amounts to union over ${\mathbb N}$ of finite sets. By contrast, we believe Definition 1.2 has not been studied in the literature. Our move away from injections/bijections towards height functions and finite sets constitutes a ‘shift of definition’ which has ample historical precedent in RM and constructive mathematics, as discussed in Remark 2.1. We note that Kleene’s quantifier $(\exists ^{2})$ from Section 1.3.2 is needed to make Definition 1.2 well-behaved, as discussed in more detail in Remark 3.5.

In more detail, we shall establish a large number of equivalences for the following principle, which is based on Definition 1.1 and expresses that $[0,1]$ is uncountable:

• • $\mathsf {NIN}_{\mathsf {alt}}$ : the unit interval is not height countable.

In particular, we show in Section 3 that $\mathsf {NIN}_{\mathsf {alt}}$ is equivalent to the following natural principles, working in Kohlenbach’s higher-order Reverse Mathematics, introduced in Section 1.3.1. Recall that a regulated function has left and right limits everywhere, as studied by Bourbaki for Riemann integration (see Section 1.3.3).

1. (i) For regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is a point $x\in [0,1]$ where f is continuous (or quasi-continuous, or lower semi-continuous, or Darboux).

2. (ii) For regulated $f:[0,1]\rightarrow {\mathbb R}$ , the set of continuity points is dense in $[0,1]$ .

3. (iii) For regulated $f:[0,1]\rightarrow [0,1]$ with Riemann integral $\int _{0}^{1}f(x)dx=0$ , there is $x\in [0,1]$ with $f(x)=0$ (Bourbaki [10, p. 61, Corollary 1]).

4. (iv) (Volterra [98]) For regulated $f,g:[0,1]\rightarrow {\mathbb R}$ , there is $x\in [0,1]$ such that f and g are both continuous or both discontinuous at x.

5. (v) (Volterra [98]) For regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is either $q\in {\mathbb Q}\cap [0,1]$ where f is discontinuous, or $x\in [0,1]\setminus {\mathbb Q}$ where f is continuous.

6. (vi) For regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is $y\in (0,1)$ where $F(x):=\lambda x.\int _{0}^{x}f(t)dt$ is differentiable with derivative equal to $f(y)$ .

7. (vii) For regulated $f:[0,1]\rightarrow {\mathbb R}$ , there are $a, b\in [0,1]$ such that $\{ x\in [0,1]:f(a)\leq f(x)\leq f(b)\}$ is infinite.

8. (viii) Blumberg’s theorem [8] restricted to regulated functions.

A full list of equivalences may be found in Section 3.3, while we obtain similar (but also very different) results for functions of bounded variation in Section 3.4. We introduce all required definitions in Section 1.3. Some of the above theorems, including items (iv) and (v) in the list, stem from Volterra’s early work (1881) in the spirit of-but predating-the Baire category theorem, as discussed in Section 1.2.

Now, comparing items (i) and (ii) suggests that our results are robust as follows:

A system is robust if it is equivalent to small perturbations of itself. [60, p. 432; emphasis in original]

Most of our results shall be seen to exhibit a similar (or stronger) level of robustness. In this light, we feel that the uncountability of ${\mathbb R}$ deserves the moniker ‘big’ system in the way this notion is used in second-order RM, namely as boasting many equivalences from various different fields of mathematics.

Next, items (i)–(viii) above imply $\mathsf {NIN}$ and are therefore hard to prove in the sense of Footnote 2. By contrast, we show in Section 3.5 that adding the extra condition ‘Baire 1’, makes these items provable from (essentially) arithmetical comprehension. While regulated functions are of course Baire 1, say over $\mathsf {ZF}$ , there is no contradiction here as the statement a regulated function on the unit interval is Baire 1 already implies $\mathsf {NIN}$ (see [72, Section 2.8]). Other restrictions of items (i)–(viii), e.g., involving semi-continuity or Baire 2, are still equivalent to $\mathsf {NIN}_{\mathsf {alt}}$ , as shown in Section 3.3.3.

Finally, this paper deals with the RM of the uncountability of ${\mathbb R}$ , while stronger ‘completeness’ properties of the reals, namely related to measure and category, are studied in [83]. In particular, the latter paper develops the higher-order RM of the Baire category theorem and Tao’s pigeon hole principle for measure spaces [93]. We do not currently know of a principle weaker than the uncountability of ${\mathbb R}$ that yields (interesting) RM-equivalences.

1.2 Volterra’s early work and related results

We introduce Volterra’s early work from [98] as it pertains to this paper, as well as related results.

First of all, the Riemann integral was groundbreaking for a number of reasons, including its ability to integrate functions with infinitely many points of discontinuity, as shown by Riemann himself [74]. A natural question is then ‘how discontinuous’ a Riemann integrable function can be. In this context, Thomae introduced the function $T:{\mathbb R}\rightarrow {\mathbb R}$ around 1875 in [95, p. 14, Section 20]:

(1.1) $$ \begin{align} T(x):= \begin{cases} 0, & \mathrm{if} \ x\in {\mathbb R}\setminus{\mathbb Q},\\ \frac{1}{q}, & \mathrm{if} \ x=\frac{p}{q} \ \mathrm{and} \ p, q \ \mathrm{are \ co}\text{-}\mathrm{prime}. \end{cases} \end{align} $$

Thomae’s function T is integrable on any interval, but has a dense set of points of discontinuity, namely ${\mathbb Q}$ , and a dense set of points of continuity, namely ${\mathbb R}\setminus {\mathbb Q}$ .

The perceptive student, upon seeing Thomae’s function as in (1.1), will ask for a function continuous at each rational point and discontinuous at each irrational one. Such a function cannot exist, as is generally proved using the Baire category theorem. However, Volterra in [98] already established this negative result about 20 years before the publication of the Baire category theorem.

Secondly, as to the content of Volterra’s paper [98], we find the following theorem on the first page, where a function is pointwise discontinuous if it has a dense set of continuity points.

Theorem 1.3 (Volterra, 1881)

There do not exist pointwise discontinuous functions defined on an interval for which the continuity points of one are the discontinuity points of the other, and vice versa.

Volterra then states two corollaries, of which the following is perhaps well-known in ‘popular mathematics’ and constitutes the aforementioned negative result.

Corollary 1.4 (Volterra, 1881)

There is no ${\mathbb R}\rightarrow {\mathbb R}$ -function that is continuous on ${\mathbb Q}$ and discontinuous on ${\mathbb R}\setminus {\mathbb Q}$ .

Thirdly, we shall study Volterra’s theorem and corollary restricted to regulated functions (see Section 1.3.3). The latter kinds of functions are automatically ‘pointwise discontinuous’ in the sense of Volterra.

Fourth, Volterra’s results from [98] are generalised in [30, 86]. The following theorem is immediate from these generalisations.

Theorem 1.5. For any countable dense set $D\subset [0,1]$ and $f:[0,1]\rightarrow {\mathbb R}$ , f is either discontinuous at some point in D or continuous at some point in $[0,1]\setminus D$ .

Perhaps surprisingly, this generalisation (restricted to bounded variation or regulated functions) is still equivalent to the uncountability of ${\mathbb R}$ . The same holds for the related Blumberg’s theorem with the same restrictions.

Theorem 1.6 (Blumberg’s theorem [8])

For any $f:{\mathbb R}\rightarrow {\mathbb R}$ , there is a dense subset $D\subset {\mathbb R}$ such that the restriction of f to D, usually denoted $f_{\upharpoonright D}$ , is continuous.

To be absolutely clear, the conclusion of Blumberg’s theorem means that

$$\begin{align*}(\forall x\in D, \varepsilon>0)(\exists \delta>0)\underline{(\forall y\in D)}(|x-y|<\delta\rightarrow |f(x)-f(y)|<\varepsilon)), \end{align*}$$

where the underlined quantifier marks the difference with ‘usual’ continuity.

1.3 Preliminaries and definitions

We briefly introduce Reverse Mathematics in Section 1.3.1. We introduce some essential axioms (Section 1.3.2) and definitions (Section 1.3.3). A full introduction may be found in, e.g., [69, Section 2].

1.3.1 Reverse Mathematics

Reverse Mathematics (RM hereafter) is a program in the foundations of mathematics initiated around 1975 by Friedman [28, 29] and developed extensively by Simpson [89]. The aim of RM is to identify the minimal axioms needed to prove theorems of ordinary, i.e., non-set theoretical, mathematics.

We refer to [91] for a basic introduction to RM and to [26, 88, 89] for an overview of RM. We expect basic familiarity with RM, in particular Kohlenbach’s higher-order RM [48] essential to this paper, including the base theory $\mathsf {RCA}_{0}^{\omega }$ . An extensive introduction can be found in, e.g., [65, 67–69]. All undefined notions may be found in [68, 69], while we do point out here that we shall sometimes use common notations from the type theory. For instance, the natural numbers are type $0$ objects, denoted $n^{0}$ or $n\in {\mathbb N}$ . Similarly, elements of Baire space are type $1$ objects, denoted $f\in {\mathbb N}^{{\mathbb N}}$ or $f^{1}$ . Mappings from Baire space ${\mathbb N}^{{\mathbb N}}$ to ${\mathbb N}$ are denoted $Y:{\mathbb N}^{{\mathbb N}}\rightarrow {\mathbb N}$ or $Y^{2}$ .

1.3.2 Some comprehension functionals

In second-order RM, the logical hardness of a theorem is measured via what fragment of the comprehension axiom is needed for a proof. For this reason, we introduce some axioms and functionals related to higher-order comprehension in this section. We are mostly dealing with conventional comprehension here, i.e., only parameters over ${\mathbb N}$ and ${\mathbb N}^{{\mathbb N}}$ are allowed in formula classes like $\Pi _{k}^{1}$ and $\Sigma _{k}^{1}$ .

First of all, the functional $\varphi $ in $(\exists ^{2})$ is also Kleene’s quantifier $\exists ^{2}$ and is clearly discontinuous at $f=11\dots $ in Cantor space:

(∃²) $$\begin{align} (\exists \varphi^{2}\leq_{2}1)(\forall f^{1})\big[(\exists n^{0})(f(n)=0) \leftrightarrow \varphi(f)=0 \big]. \end{align}$$

In fact, $(\exists ^{2})$ is equivalent to the existence of $F:{\mathbb R}\rightarrow {\mathbb R}$ such that $F(x)=1$ if $x>_{{\mathbb R}}0$ , and $0$ otherwise (see [48, Proposition 3.12]). Related to $(\exists ^{2})$ , the functional $\mu ^{2}$ in $(\mu ^{2})$ is called Feferman’s $\mu $ (see [2]) and may be found—with the same symbol—in Hilbert-Bernays’ Grundlagen [35, Supplement IV]:

(μ²) $$\begin{align} (\exists \mu^{2})(\forall f^{1})\big[ (\exists n)(f(n)=0) \rightarrow [f(\mu(f))=0&\wedge (\forall i<\mu(f))(f(i)\ne 0) ]\\ & \wedge [ (\forall n)(f(n)\ne0)\rightarrow \mu(f)=0] \big]. \end{align}$$

We have $(\exists ^{2})\leftrightarrow (\mu ^{2})$ over $\mathsf {RCA}_{0}^{\omega }$ (see [48, Section 3]) and $\mathsf {ACA}_{0}^{\omega }\equiv \mathsf {RCA}_{0}^{\omega }+(\exists ^{2})$ proves the same sentences as $\mathsf {ACA}_{0}$ by [38, Theorem 2.5].

Secondly, the functional $\mathsf {S}^{2}$ in $(\mathsf {S}^{2})$ is called the Suslin functional [48]:

(S²) $$\begin{align} (\exists\mathsf{S}^{2}\leq_{2}1)(\forall f^{1})\big[ (\exists g^{1})(\forall n^{0})(f(\overline{g}n)=0)\leftrightarrow \mathsf{S}(f)=0 \big]. \end{align}$$

The system $\Pi _{1}^{1}\text {-}\mathsf {CA}_{0}^{\omega }\equiv \mathsf {RCA}_{0}^{\omega }+(\mathsf {S}^{2})$ proves the same $\Pi _{3}^{1}$ -sentences as $\Pi _{1}^{1}\text {-}\mathsf {CA}_{0}$ by [76, Theorem 2.2]. By definition, the Suslin functional $\mathsf {S}^{2}$ can decide whether a $\Sigma _{1}^{1}$ -formula as in the left-hand side of $(\mathsf {S}^{2})$ is true or false. We similarly define the functional $\mathsf {S}_{k}^{2}$ which decides the truth or falsity of $\Sigma _{k}^{1}$ -formulas from $\mathsf {L}_{2}$ ; we also define the system $\Pi _{k}^{1}\text {-}\mathsf {CA}_{0}^{\omega }$ as $\mathsf {RCA}_{0}^{\omega }+(\mathsf {S}_{k}^{2})$ , where $(\mathsf {S}_{k}^{2})$ expresses that $\mathsf {S}_{k}^{2}$ exists. We note that the operators $\nu _{n}$ from [18, p. 129] are essentially $\mathsf {S}_{n}^{2}$ strengthened to return a witness (if existent) to the $\Sigma _{n}^{1}$ -formula at hand.

Thirdly, full second-order arithmetic $\mathsf {Z}_{2}$ is readily derived from $\cup _{k}\Pi _{k}^{1}\text {-}\mathsf {CA}_{0}^{\omega }$ , or from:

(∃³) $$\begin{align} (\exists E^{3}\leq_{3}1)(\forall Y^{2})\big[ (\exists f^{1})(Y(f)=0)\leftrightarrow E(Y)=0 \big], \end{align}$$

and we therefore define $\mathsf {Z}_{2}^{\Omega }\equiv \mathsf {RCA}_{0}^{\omega }+(\exists ^{3})$ and $\mathsf {Z}_{2}^\omega \equiv \cup _{k}\Pi _{k}^{1}\text {-}\mathsf {CA}_{0}^{\omega }$ , which are conservative over $\mathsf {Z}_{2}$ by [38, Corollary 2.6]. Despite this close connection, $\mathsf {Z}_{2}^{\omega }$ and $\mathsf {Z}_{2}^{\Omega }$ can behave quite differently, as discussed in, e.g., [65, Section 2.2]. The functional from $(\exists ^{3})$ is also called ‘ $\exists ^{3}$ ’, and we use the same convention for other functionals.

1.3.3 Some basic definitions

We introduce some definitions needed in the below, mostly stemming from mainstream mathematics. We note that subsets of ${\mathbb R}$ are given by their characteristic functions as in Definition 1.7, well-known from measure and probability theory.

Zeroth of all, we make use the usual definition of (open) set, where $B(x, r)$ is the open ball with radius $r>0$ centred at $x\in {\mathbb R}$ .

Definition 1.7 (Sets)

• • A subset $A\subset {\mathbb R}$ is given by its characteristic function $F_{A}:{\mathbb R}\rightarrow \{0,1\}$ , i.e., we write $x\in A$ for $ F_{A}(x)=1$ , for any $x\in {\mathbb R}$ .

• • A subset $O\subset {\mathbb R}$ is open in case $x\in O$ implies that there is $k\in {\mathbb N}$ such that $B(x, \frac {1}{2^{k}})\subset O$ .

• • A subset $C\subset {\mathbb R}$ is closed if the complement ${\mathbb R}\setminus C$ is open.

As discussed in Remark 2.7, the study of functions of bounded variation already gives rise to open sets that do not come with additional representation beyond Definition 1.7.

First of all, we shall study the following notions of weak continuity, all of which hark back to the days of Baire, Darboux, and Volterra [3, 4, 22, 98].

Definition 1.8. For $f:[0,1]\rightarrow {\mathbb R}$ , we have the following definitions:

• • f is upper semi-continuous at $x_{0}\in [0,1]$ if $f(x_{0})\geq _{{\mathbb R}}\lim \sup _{x\rightarrow x_{0}} f(x)$ .

• • f is lower semi-continuous at $x_{0}\in [0,1]$ if $f(x_{0})\leq _{{\mathbb R}}\lim \inf _{x\rightarrow x_{0}} f(x)$ .

• • f is quasi-continuous at $x_{0}\in [0, 1]$ if for $ \epsilon> 0$ and an open neighbourhood U of $x_{0}$ , there is a non-empty open ${ G\subset U}$ with $(\forall x\in G) (|f(x_{0})-f(x)|<\varepsilon )$ .

• • $f:{\mathbb R}\rightarrow {\mathbb R}$ symmetrically continuous at $x\in {\mathbb R}$ if

  $$\begin{align*}(\forall \varepsilon> 0)(\exists \delta>0)(\forall z\in {\mathbb R} )(|z|<\delta\rightarrow |f(x+z)-f(x-z)|<\varepsilon ). \end{align*}$$

• • f is Baire 1 if it is the pointwise limit of a sequence of continuous functions.

• • f is Baire $2$ if it is the pointwise limit of a sequence of Baire $1$ functions.

• • f is Baire 1 $^{*}$ if ³ there is a sequence of closed sets $(C_{n})_{n\in {\mathbb N}}$ such $[0,1]=\cup _{n\in {\mathbb N}}C_{n}$ and $f_{\upharpoonright C_{m}}$ is continuous for all $m\in {\mathbb N}$ .

The first two items are often abbreviated as ‘usco’ and ‘lsco’.

Secondly, we also need the notion of ‘intermediate value property’, also called the ‘Darboux property’ in light of Darboux’s work in [22].

Definition 1.9 (Darboux property)

Let $f:[0,1]\rightarrow {\mathbb R}$ be given.

• • A real $y\in {\mathbb R}$ is a left (resp. right) cluster value of f at $x\in [0,1]$ if there is $(x_{n})_{n\in {\mathbb N}}$ such that $y=\lim _{n\rightarrow \infty } f(x_{n})$ and $x=\lim _{n\rightarrow \infty }x_{n}$ and $(\forall n\in {\mathbb N})(x_{n}\leq x)$ (resp. $(\forall n\in {\mathbb N})(x_{n}\geq x)$ ).

• • A point $x\in [0,1]$ is a Darboux point of $f:[0,1]\rightarrow {\mathbb R}$ if for any $\delta>0$ and any left (resp. right) cluster value y of f at x and $z\in {\mathbb R}$ strictly between y and $f(x)$ , there is $w\in (x-\delta , x)$ (resp. $w\in ( x, x+\delta )$ ) such that $f(w)=y$ .

By definition, a point of continuity is also a Darboux point, but not vice versa.

Thirdly, we introduce the ‘usual’ definitions of countable set (Definitions 1.10 and 1.11).

Definition 1.10 (Enumerable sets of reals)

A set $A\subset {\mathbb R}$ is enumerable if there exists a sequence $(x_{n})_{n\in {\mathbb N}}$ such that $(\forall x\in {\mathbb R})(x\in A\rightarrow (\exists n\in {\mathbb N})(x=_{{\mathbb R}}x_{n}))$ .

This definition reflects the RM-notion of ‘countable set’ from [89, Theorem V.4.2]. We note that given $\mu ^{2}$ from Section 1.3.2, we may replace the final implication in Definition 1.10 by an equivalence.

Definition 1.11 (Countable subset of ${\mathbb R}$ )

A set $A\subset {\mathbb R}$ is countable if there exists $Y:{\mathbb R}\rightarrow {\mathbb N}$ such that $(\forall x, y\in A)(Y(x)=_{0}Y(y)\rightarrow x=_{{\mathbb R}}y)$ . The mapping $Y:{\mathbb R}\rightarrow {\mathbb N}$ is called an injection from A to ${\mathbb N}$ or injective on A. If $Y:{\mathbb R}\rightarrow {\mathbb N}$ is also surjective, i.e., $(\forall n\in {\mathbb N})(\exists x\in A)(Y(x)=n)$ , we call A strongly countable.

The first part of Definition 1.11 is from Kunen’s set theory textbook [54, p. 63] and the second part is taken from Hrbacek–Jech’s set theory textbook [36] (where the term ‘countable’ is used instead of ‘strongly countable’). For the rest of this paper, ‘strongly countable’ and ‘countable’ shall exclusively refer to Definition 1.11, except when explicitly stated otherwise.

Finally, the uncountability of ${\mathbb R}$ can be studied in numerous guises in higher-order RM. For instance, the following are from [68, 69], where it is also shown that many extremely basic theorems imply these principles, while $\mathsf {Z}_{2}^{\omega }$ cannot prove them.

• • For a countable set $A\subset [0,1]$ , there is $y\in [0,1]\setminus A$ .

• • $\mathsf {NIN}$ : there is no injection from $[0,1]$ to ${\mathbb N}$ .

• • For a strongly countable set $A\subset [0,1]$ , there is $y\in [0,1]\setminus A$ .

• • $\mathsf {NBI}$ : there is no bijection from $[0,1]$ to ${\mathbb N}$ .

The reader will verify that the first two and last two items are (trivially) equivalent. Besides these and similar variations in [79], we have not been able to obtain elegant or natural equivalences involving the uncountability of ${\mathbb R}$ try as we might. As discussed in Section 2, this is because the above items are formulated using the ‘set theoretic’ definition of countability as in Definition 1.11. In Section 3, we obtain many equivalences involving the uncountability of ${\mathbb R}$ , based on the alternative (but equivalent over $\mathsf {ZF}$ ) notion of ‘height countable’ introduced in Section 1.1.

1.3.4 Some advanced definitions: bounded variation and around

We formulate the definitions of bounded variation and regulated functions, and some background.

Firstly, the notion of bounded variation (often abbreviated $BV$ below) was first explicitly ⁴ introduced by Jordan around 1881 [42] yielding a generalisation of Dirichlet’s convergence theorems for Fourier series. Indeed, Dirichlet’s convergence results are restricted to functions that are continuous except at a finite number of points, while $BV$ -functions can have infinitely many points of discontinuity, as already studied by Jordan, namely in [42, p. 230]. Nowadays, the total variation of a function $f:[a, b]\rightarrow {\mathbb R}$ is defined as follows:

(1.2) $$ \begin{align}\textstyle V_{a}^{b}(f):=\sup_{a\leq x_{0}< \dots< x_{n}\leq b}\sum_{i=0}^{n} |f(x_{i})-f(x_{i+1})|. \end{align} $$

If this quantity exists and is finite, one says that f has bounded variation on $[a,b]$ . Now, the notion of bounded variation is defined in [64] without mentioning the supremum in (1.2); this approach can also be found in [11, 12, 53]. Hence, we shall distinguish between the two notions in Definition 1.12. As it happens, Jordan seems to use item (a) of Definition 1.12 in [42, pp. 228–229]. This definition suggests a twofold variation for any result on functions of bounded variation, namely depending on whether the supremum (1.2) is given, or only an upper bound on the latter.

Definition 1.12 (Variations on variation)

1. (a) The function $f:[a,b]\rightarrow {\mathbb R}$ has bounded variation on $[a,b]$ if there is $k_{0}\in {\mathbb N}$ such that $k_{0}\geq \sum _{i=0}^{n} |f(x_{i})-f(x_{i+1})|$ for any partition $x_{0}=a <x_{1}< \dots < x_{n-1}<x_{n}=b $ .

2. (b) The function $f:[a,b]\rightarrow {\mathbb R}$ has a variation on $[a,b]$ if the supremum in (1.2) exists and is finite.

Secondly, the fundamental theorem about $BV$ -functions is as follows; this theorem is proved by Jordan in [42].

Theorem 1.13 (Jordan decomposition theorem [42, p. 229])

A $BV$ -function $f : [0, 1] \rightarrow {\mathbb R}$ is the difference of two non-decreasing functions $g, h:[0,1]\rightarrow {\mathbb R}$ .

Theorem 1.13 has been studied via second-order representations in [31, 53, 64, 105]. The same holds for constructive analysis by [11, 12, 33, 73], involving different (but related) constructive enrichments. Now, $\mathsf {ACA}_{0}$ suffices to derive Theorem 1.13 for various kinds of second-order representations of $BV$ -functions in [53, 64]. By contrast, our results in [68] imply that the third-order version of Theorem 1.13 is hard to prove in terms of conventional comprehension.

Thirdly, Jordan proves in [43, Section 105] that $BV$ -functions are exactly those for which the notion of ‘length of the graph of the function’ makes sense. In particular, $f\in BV$ if and only if the ‘length of the graph of f’, defined as follows:

(1.3) $$ \begin{align}\textstyle L(f, [0,1]):=\sup_{0=t_{0}<t_{1}<\dots <t_{m}=1} \sum_{i=0}^{m-1} \sqrt{(t_{i}-t_{i+1})^{2}+(f(t_{i})-f(t_{i+1}))^{2} } \end{align} $$

exists and is finite by [1, Theorem 3.28(c)]. In case the supremum in (1.3) exists (and is finite), f is also called rectifiable. Rectifiable curves predate $BV$ -functions: in [84, Section 1 and 2], it is claimed that (1.3) is essentially equivalent to Duhamel’s 1866 approach from [25, Chapter VI]. Around 1833, Dirksen, the PhD supervisor of Jacobi and Heine, already provides a definition of arc length that is (very) similar to (1.3) (see [24, Section 2, p. 128], but with some conceptual problems as discussed in [20, Section 3].

Fourth, a function is regulated (called ‘regular’ in [1]) if for every $x_{0}$ in the domain, the ‘left’ and ‘right’ limits $f(x_{0}-)=\lim _{x\rightarrow x_{0}-}f(x)$ and $f(x_{0}+)=\lim _{x\rightarrow x_{0}+}f(x)$ exist. Scheeffer studies discontinuous regulated functions in [84] (without using the term ‘regulated’), while Bourbaki develops Riemann integration based on regulated functions in [9]. We note that $BV$ -functions are regulated, while Weierstrass’ ‘monster’ function is a natural example of a regulated function not in $BV$ .

Finally, an interesting observation about regulated functions is as follows.

Remark 1.14 (Continuity and regulatedness)

First of all, as discussed in [48, Section 3], the local equivalence for functions on Baire space between sequential and ‘epsilon-delta’ continuity cannot be proved in $\mathsf {ZF}$ . By [68, Theorem 3.32], this equivalence for regulated functions is provable in $\mathsf {ZF}$ (and actually just $\mathsf {ACA}_{0}^{\omega }$ ).

Secondly, $\mu ^{2}$ readily computes the left and right limits of regulated $f:[0,1]\rightarrow {\mathbb R}$ . In this way, the formula ‘f is continuous at $x\in [0,1]$ ’ is decidable using $\mu ^{2}$ , namely equivalent to the formula ‘ $f(x+)=f(x)=f(x-)$ ’. The usual ‘epsilon-delta’ definition of continuity involves quantifiers over ${\mathbb R}$ , i.e., the previous equality is much simpler and more elementary.

By the previous remark, the basic notions needed for the study of regulated and $BV$ -functions make sense in $\mathsf {ACA}_{0}^{\omega }$ .

2 Countability by any other name

We show that the ‘standard’ set-theoretic definitions of countability-from Section 1.3.3 and based on injections and bijections to ${\mathbb N}$ -are not suitable for the RM-study of regulated functions (see Section 2.1) and $BV$ -functions (Section 2.2). We also formulate an alternative-more suitable for RM-notion of countability (Definitions 2.3 and 2.6), which amounts to ‘unions over ${\mathbb N}$ of finite sets’ and which can also be found in the mathematical literature. This kind of ‘shift of definition’ has historical precedent as follows.

Remark 2.1. First of all, the correct choice of definition for a given mathematical notion is crucial to the development of RM, as can be gleaned from the following quote from [15, p. 129].

Under the old definition [of real number from [87]], it would be consistent with $\mathsf {RCA}_{0}$ that there exists a sequence of real numbers $(x_{n})_{n\in {\mathbb N}}$ such that $(x_{n}+\pi )_{n\in {\mathbb N}}$ is not a sequence of real numbers. We thank Ian Richards for pointing out this defect of the old definition. Our new definition [of real number from [15]], given above, is adopted in order to remove this defect. All of the arguments and results of [87] remain correct under the new definition.

In short, the early definition of ‘real number’ from [87] was not suitable for the development of RM, highlighting the importance of the ‘right’ choice of definition.

Secondly, we stress that RM is not unique in this regard: the early definition of ‘continuous function’ in Bishop’s constructive analysis [7] was also deemed problematic and changed to a new definition to be found in [13]; the (substantial) problems with both definitions are discussed in some detail in [14, 99], including elementary properties such as the concatenation of continuous functions and the continuity of $\frac {1}{x}$ for $x>0$ .

In short, the development of mathematics in logical systems with ‘restricted’ resources, like RM or constructive mathematics, seems to hinge on the ‘right’ choice of definition. In this section, we argue that the ‘right’ definition of countability for higher-order RM is given by height functions as in Section 1.1. To be absolutely clear, the background theory for this section is $\mathsf {ZFC}$ , i.e., a statement like ‘ $A\subset {\mathbb R}$ is countable’ means that the latter is provable in the former; most arguments (should) go through in $\mathsf {Z}_{2}^{\Omega }$ .

2.1 Regulated functions and countability

As suggested in Section 1.1, the set-theoretic definition of countable set is not suitable for the RM-study of regulated functions. We first provide some motivation for this claim in Remark 2.2. Inspired by the latter, we can then present our alternative notion in Definition 2.3, which amounts to ‘unions over ${\mathbb N}$ of finite sets’.

Remark 2.2 (Countable sets by any other name)

First of all, we have previously investigated the RM of regulated functions in [68]. As part of this study, the following sets—definable via $\exists ^{2}$ —present themselves, where $f:[0,1]\rightarrow {\mathbb R}$ is regulated:

(2.1) $$ \begin{align}\textstyle &A:= \big\{x\in (0,1): f(x+)\ne f(x) \vee f(x-)\ne f(x)\big\}, \notag \\ &A_{n}:=\big\{x\in (0,1): |f(x+)- f(x)|>\tfrac1{2^{n}} \vee |f(x-)- f(x)|>\tfrac1{2^{n}}\big\}. \end{align} $$

Clearly, $A=\cup _{n\in {\mathbb N}}A_{n}$ collects all points in $(0,1)$ where f is discontinuous; this set is central to many proofs involving regulated functions (see, e.g., [1, Theorem 0.36]). Now, that $A_{n}$ is finite follows by a standard ⁵ compactness argument. However, while A is then countable, we are unable to construct an injection from A to ${\mathbb N}$ (let alone a bijection), even working in $\mathsf {Z}_{2}^{\omega }$ (see Remark 2.7 for details).

In short, one readily finds countable sets ‘in the wild’, namely pertaining to regulated functions, for which the associated injections to ${\mathbb N}$ cannot be constructed in reasonably weak logical systems.

Secondly, in light of (2.1), regulated functions give rise to countable sets given only as the union over ${\mathbb N}$ of finite sets (i.e., without information about an injection to ${\mathbb N}$ ). To see that the ‘reverse’ is also true, consider the following function:

(2.2) $$ \begin{align} h(x):= \begin{cases} 0, & x\not \in \cup_{m\in {\mathbb N}}X_{m}, \\ \frac{1}{2^{n+1}}, & x\in X_{n} \text{ and } n \text{ is the least such number,} \end{cases} \end{align} $$

where $(X_{n})_{n\in {\mathbb N}}$ is a sequence of finite sets in $[0,1]$ . One readily shows that h is regulated using $\exists ^{2}$ . For general closed sets, (2.2) is crucial to the study of Baire 1 functions (see [63, p. 238]). Hence, regulated functions yield countable sets given (only) as unions over ${\mathbb N}$ of finite sets, namely via $A=\cup _{n\in {\mathbb N}}A_{n}$ from (2.1), and vice versa, namely via $h:[0,1]\rightarrow {\mathbb R}$ as in (2.2).

In summary, we observe that the usual definition of countable set (involving injections/bijections to ${\mathbb N}$ ) is not suitable for the RM-study of regulated functions. Luckily, (2.1) and (2.2) suggest an alternative approach via the fundamental connection between regulated functions on one hand, and countable sets given as

$$ \begin{align*} \mathit{the \ union \ over} \ {\mathbb N} \ \mathit{of \ finite \ sets} \end{align*} $$

on the other hand. In conclusion, the RM-study of regulated functions should be based on the centred notion of countability and not injections/bijections to ${\mathbb N}$ .

Motivated by Remark 2.2, we introduce our alternative definition of countability, which is exactly the same as Definition 1.1 in Section 1.1.

Definition 2.3. A set $A\subset {\mathbb R}$ is height countable if there is a height function $H:{\mathbb R}\rightarrow {\mathbb N}$ for A, i.e., for all $n\in {\mathbb N}$ , $A_{n}:= \{ x\in A: H(x)<n\}$ is finite.

The previous notion of ‘height’ is mentioned in the context of countability in, e.g., [40, 49, 59, 75, 97]. Definition 2.3 amounts to ‘union over ${\mathbb N}$ of finite sets’, as is readily shown in $\mathsf {ACA}_{0}^{\omega }$ .

Finally, the observations from Remark 2.2 regarding countable sets also apply mutatis mutandis to finite sets. Indeed, finite as each $A_{n}$ from (2.1) may be, we are unable to construct an injection to a finite subset of ${\mathbb N}$ , even assuming $\mathsf {Z}_{2}^{\omega }$ (see Remark 2.7 for details). By contrast, the definition of finite set from Section 1.1 is more suitable: one readily ⁶ shows that $A_{n}$ from (2.1) is finite as in Definition 2.4, which is exactly the same as Definition 1.2 in Section 1.1.

Definition 2.4 (Finite set)

Any $X\subset {\mathbb R}$ is finite if there is $N\in {\mathbb N}$ such that for any finite sequence $(x_{0}, \dots , x_{N})$ of distinct reals, there is $i\leq N$ such that $x_{i}\not \in X$ .

The number N from Definition 2.4 is call a size bound for the finite set $X\subset {\mathbb R}$ . Analogous to countable sets, the RM-study of regulated functions should be based on Definition 2.4 and not on the set-theoretic definition based on injections/bijections to finite subsets of ${\mathbb N}$ or similar constructs.

2.2 Bounded variation functions and countability

We discuss the observations from Section 2.1 for the particular case of functions of bounded variation (which are regulated by Theorem 3.3). In particular, while the same observations apply, they have to be refined to yield elegant equivalences.

Remark 2.5 (Countable by another name)

First of all, we consider (2.1), but formulated for a $BV$ -function $g:[0,1]\rightarrow {\mathbb R}$ , as follows:

(2.3) $$ \begin{align}\textstyle &B:= \big\{x\in (0,1): g(x+)\ne g(x) \vee g(x-)\ne g(x)\big\}, \notag \\ &B_{n}:=\big\{x\in (0,1): |g(x+)- g(x)|>\tfrac1{2^{n}} \vee |g(x-)- g(x)|>\tfrac1{2^{n}}\big\}. \end{align} $$

Similar to $A=\cup _{n\in }A_{n}$ as in (2.3), $B=\cup _{n\in {\mathbb N}}B_{n}$ collects all points in $(0,1)$ where g is discontinuous and this set is central to many proofs involving $BV$ -functions (see [1]). Similar to A from (2.3), B is countable but we are unable to construct an injection from B to ${\mathbb N}$ (let alone a bijection), even assuming $\mathsf {Z}_{2}^{\omega }$ (see Remark 2.7).

Secondly, there is a crucial difference between (2.1) and (2.3): we know that the set $B_{n}$ is finite and has at most $2^{n}V_{0}^{1}(f)$ elements; indeed, each element of $B_{n}$ contributes at least $1/2^{n}$ to the total variation $V_{0}^{1}(f)$ as in (1.2). By contrast, we have no extra information about the size of $A_{n}$ from (2.1). However, this extra information is crucial if we wish to deal with $BV$ -functions (only). Indeed, the function h from (2.2) is not in $BV$ , e.g., in the trivial case where each $X_{n}$ has at least $2^{n+1}$ elements. By contrast, consider the following nicer function:

(2.4) $$ \begin{align} k(x):= \begin{cases} 0, & x\not \in \cup_{m\in {\mathbb N}}Y_{m}, \\ \frac{1}{2^{n+1}} \frac{1}{g(n)+1},& x\in Y_{n} \text{ and } n \text{ is the least such number}, \end{cases} \end{align} $$

where $g\in {\mathbb N}^{{\mathbb N}}$ is a width function ⁷ for $(Y_{n})_{n\in {\mathbb N}}$ . One readily verifies that $k:[0,1]\rightarrow {\mathbb R}$ is in $BV$ with total variation bounded by $1$ . Hence, $BV$ -functions yield countable sets given (only) as in the following description:

$$ \begin{align*} \mathit{unions \ over} \ {\mathbb N} \ \mathit{of \ finite \ sets \ with \ a \ width \ function,} \end{align*} $$

namely via $B=\cup _{n\in {\mathbb N}}B_{n}$ from (2.3), and vice versa, namely via $k:[0,1]\rightarrow {\mathbb R}$ as in (2.4). The generalisations of bounded variation from Remark 3.23 have a similar property, as evidenced by the final part of the proof of Theorem 3.20.

Motivated by Remark 2.5, we introduce our alternative (equivalent over $\mathsf {ZF}$ ) definition of countability for the RM-study of $BV$ -functions.

Definition 2.6. A set $B\subset {\mathbb R}$ is height–width countable if there is a height function $H:{\mathbb R}\rightarrow {\mathbb N}$ and width function $g:{\mathbb N}\rightarrow {\mathbb N}$ , i.e., for all $n\in {\mathbb N}$ , the set $B_{n}:= \{ x\in B: H(x)<n\}$ is finite with size bound $g(n)$ .

Finally, the following technical remark makes the claims in Remarks 2.2 and 2.5 more precise in terms of logical systems.

Remark 2.7. As discussed above, the sets $A_{n}$ from (2.1) and $B_{n}$ from (2.3) are finite, while the unions $A=\cup _{n\in {\mathbb N}}A_{n}$ and $B=\cup _{n\in {\mathbb N}}B_{n}$ are countable. Hence, working in $\mathsf {ZF}$ (or even $\mathsf {Z}_{2}^{\Omega }$ from Section 1.3.2), the following objects can be constructed:

• • for $n\in {\mathbb N}$ , an injection $Y_{n}$ from $A_{n}$ to some $\{0, 1, \dots , k\}$ with $k\in {\mathbb N}$ ,

• • for $m\in {\mathbb N}$ , an RM-code $C_{m}$ (see [89, II.5.6]) for the closed sets $A_{m}$ or $B_{m}$ .

However, it is shown in [81, 82] that neither $Y_{n}$ nor $C_{n}$ are computable (in the sense of Kleene S1–S9; see [58]) in terms of any $\mathsf {S}_{m}^{2}$ and the other data. As a result, even $\mathsf {Z}_{2}^{\omega }$ cannot prove the general existence of $Y_{n}$ and $C_{n}$ as in the previous items. By contrast, the system $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ (and even fragments) suffice to show that Definitions 2.3, 2.6, and 2.4 apply to $A,A_{n}$ from (2.1) and $B,B_{n}$ from (2.3).

In conclusion, we have introduced ‘new’—but equivalent over $\mathsf {ZF}$ and the weaker $\mathsf {Z}_{2}^{\Omega }$ —definitions of finite and countable set with the following properties.

• • Our ‘new’ definitions capture the notion of finite and countable set as it occurs ‘in the wild’, namely in the study of $BV$ or regulated functions. This holds over relatively weak systems by Remark 2.7.

• • One finds our ‘new’ definitions, in particular the notion of ‘height’, in the literature (see [40, 49, 59, 75, 97]).

• • These ‘new’ definitions shall be seen to yield many equivalences in the RM of the uncountability of ${\mathbb R}$ (Sections 3.3 and 3.4).

We believe that the previous items justify our adoption of our ‘new’ definitions of finite and countable set. Moreover, Remark 2.1 creates some historical precedent based on second-order RM and constructive mathematics.

3 Main results: regulated and $BV$ -functions

3.1 Introduction

In this section, we establish the equivalences sketched in Section 1.1 pertaining to the uncountability of ${\mathbb R}$ and properties of regulated functions (Section 3.3) and $BV$ -functions (Section 3.4). In Section 3.2, we establish some basic properties of $BV$ and regulated functions in weak systems.

As noted in Section 1.1, we shall show that the uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}$ is robust, i.e., equivalent to small perturbations of itself [60, p. 432]. Striking examples of this claimed robustness may be found in Theorem 3.7, where the perturbations are given by considering either one point of continuity, a dense set of such points, or various uncountability criteria for $C_{f}$ , the set of continuity points.

Finally, the content of Section 3.5 is explained in the following remark.

Remark 3.1 (When more is less)

As noted in Section 1.1, $\mathsf {NIN}_{\mathsf {alt}}$ is equivalent to well-known theorems from analysis restricted to regulated functions, with similar results for $BV$ -functions. These (restricted) theorems thus imply $\mathsf {NIN}$ and are not provable in $\mathsf {Z}_{2}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ as a result (see [69]). We show in Section 3.5 that adding the extra condition ‘Baire 1’ to these theorems makes them provable from (essentially) arithmetical comprehension. While regulated and $BV$ -functions are Baire 1, say over $\mathsf {ZF}$ or $\mathsf {Z}_{2}^{\Omega }$ , there is no contradiction here as the statement

$$ \begin{align*} \mathit{a} \ BV\text{-}\mathit{function \ on \ the \ unit \ interval \ is \ Baire \ 1} \end{align*} $$

already implies $\mathsf {NIN}$ by [72, Theorem 2.34]. We stress that ‘Baire 1’ is special in this regard: other restrictions, e.g., involving semi-continuity or Baire 2, yield theorems that are still equivalent to $\mathsf {NIN}_{\mathsf {alt}}$ , as shown in Section 3.3.3. We have no explanation for this phenomenon.

3.2 Preliminary results

We collect some preliminary results pertaining to regulated and $BV$ -functions, and $\mathsf {NIN}_{\mathsf {alt}}$ from Section 1.1.

First of all, to allow for a smooth treatment of finite sets, we shall adopt the following principle that collects the most basic properties of finite sets.

Principle 3.2 ( $\mathsf {FIN}$ )

• • Finite union theorem: for a sequence of finite sets $(X_{n})_{n\in {\mathbb N}}$ and any $k\in {\mathbb N}$ , $\cup _{n\leq k}X_{n}$ is finite.

• • For any finite $X\subset {\mathbb R}$ , there is a finite sequence of reals $(x_{0}, \dots , x_{k})$ that includes all elements of X.

• • Finite Axiom of Choice: for $Y^{2}, k^{0}$ with $(\forall n\leq k)(\exists f\in 2^{{\mathbb N}})(Y(f, n)=0)$ , there is a finite sequence $(f_{0}, \dots , f_{k})$ in $2^{{\mathbb N}}$ with $(\forall n\leq k)(Y(f_{n}, n)=0)$ .

One can readily derive $\mathsf {FIN}$ from a sufficiently general fragment of the induction axiom; the RM of the latter is well-known (see, e.g., [89, X.4.4]) and the RM of (fragments of) $\mathsf {FIN}$ is therefore a matter of future research. We note that in [68], we could derive (fragments of) $\mathsf {FIN}$ from the principles under study, like the fact that (height) countable sets of reals can be enumerated. Hence, we could mostly avoid the use of fragments of $\mathsf {FIN}$ in the base theory in [68], which does not seem possible for this paper.

Secondly, we need some some basic properties of $BV$ and regulated functions, all of which have been established in [68] already.

Theorem 3.3 ( $\mathsf {ACA}_{0}^{\omega }$ )

• • Assuming $\mathsf {FIN}$ , any $BV$ -function $f:[0,1]\rightarrow {\mathbb R}$ is regulated.

• • Any monotone function $f:[0,1]\rightarrow {\mathbb R}$ has bounded variation.

• • For any monotone function $f:[0,1]\rightarrow {\mathbb R}$ , there is a sequence $(x_{n})_{n\in {\mathbb N}}$ that enumerates all $x\in [0,1]$ such that f is discontinuous at x.

• • For regulated $f:[0,1]\rightarrow {\mathbb R}$ and $x\in [0,1]$ , f is sequentially continuous at x if and only if f is epsilon-delta continuous at x.

• • For finite $X\subset [0,1]$ , the function $\mathbb {1}_{X}$ has bounded variation.

Proof Proofs may be found in [68, Section 3.3].

The fourth item of Theorem 3.3 is particularly interesting as the local equivalence between sequential and epsilon-delta continuity for general ${\mathbb R}\rightarrow {\mathbb R}$ -functions is not provable in $\mathsf {ZF}$ , while $\mathsf {RCA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ suffices, as discussed in Remark 1.14.

Thirdly, we discuss some ‘obvious’ equivalences for $\mathsf {NIN}$ and $\mathsf {NBI}$ .

Remark 3.4. Now, $\mathsf {NIN}$ and $\mathsf {NBI}$ are formulated for mappings from $[0,1]$ to ${\mathbb N}$ , but we can equivalently replace the unit interval by, e.g., ${\mathbb R}$ , $2^{{\mathbb N}}$ , and ${\mathbb N}^{{\mathbb N}}$ , as shown in [79, Section 2.1]. An important observation in this context, and readily formalised in $\mathsf {ACA}_{0}^{\omega }$ , is that the (rescaled) tangent function provides a bijection from any open interval to ${\mathbb R}$ ; the inverse of tangent, called arctangent, yields a bijection in the other direction (also with rescaling). Moreover, using these bijections, one readily shows that $\mathsf {NIN}_{\mathsf {alt}}$ is equivalent to the following:

• • there is no height function from ${\mathbb R}$ to ${\mathbb N}$ .

Similarly, if we can show that there is no height function from some fixed open interval to ${\mathbb N}$ , then $\mathsf {NIN}_{\mathsf {alt}}$ follows. We will tacitly make use of this fact in the proof of Theorems 3.6 and 3.7.

Fourth, while we choose to use (at least) the system $\mathsf {ACA}_{0}^{\omega }$ as our base theory, one can replace the latter by $\mathsf {RCA}_{0}^{\omega }$ using the following trick.

Remark 3.5 (Excluded middle trick)

The law of excluded middle as in $(\exists ^{2})\vee \neg (\exists ^{2})$ is quite useful as follows: suppose we are proving $T\rightarrow \mathsf {NIN}_{\mathsf {alt}}$ over $\mathsf {RCA}_{0}^{\omega }$ . Now, in case $\neg (\exists ^{2})$ , all functions on ${\mathbb R}$ are continuous by [48, Proposition 3.12] and $\mathsf {NIN}_{\mathsf {alt}}$ then trivially ⁸ holds. Hence, what remains is to establish $T\rightarrow \mathsf {NIN}_{\mathsf {alt}}$ in case we have $(\exists ^{2})$ . However, the latter axiom, e.g., implies $\mathsf {ACA}_{0}$ and can uniformly convert reals to their binary representations. In this way, finding a proof in $\mathsf {RCA}_{0}^{\omega }+(\exists ^{2})$ is ‘much easier’ than finding a proof in $\mathsf {RCA}_{0}^{\omega }$ . In a nutshell, we may without loss of generality assume $(\exists ^{2})$ when proving theorems that are trivial (or readily proved) when all functions (on ${\mathbb R}$ or ${\mathbb N}^{{\mathbb N} }$ ) are continuous, like $\mathsf {NIN}_{\mathsf {alt}}$ . Moreover, we can replace $2^{{\mathbb N}}$ by $[0,1]$ at will, which is convenient sometimes.

While the previous trick is useful, it should be used sparingly: the axiom $(\exists ^{2})$ is required to guarantee that basic sets like the unit interval are sets in our sense (Definition 1.7) or that finite sets (Definition 1.2) are well-behaved. For this reason, we only mention Remark 3.5 in passing and shall generally work over $\mathsf {ACA}_{0}^{\omega }$ .

3.3 Regulated functions and the uncountability of ${\mathbb R}$

We establish the equivalences sketched in Section 1.1 pertaining to the uncountability of ${\mathbb R}$ and properties of regulated functions.

3.3.1 Volterra’s early work

In this section, we connect the uncountability of ${\mathbb R}$ to Volterra’s early results from Section 1.2. In particular, we establish the following theorem where the final two items exhibit some nice robustness properties of $\mathsf {NIN}_{\mathsf {alt}}$ and Volterra’s results, as promised in Section 1.1.

Theorem 3.6 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}+\mathsf {FIN}$ )

The following are equivalent.

1. (a) The uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}$ .

2. (b) Volterra’s theorem for regulated functions: there do not exist two regulated functions defined on the unit interval for which the continuity points of one are the discontinuity points of the other, and vice versa.

3. (c) Volterra’s corollary for regulated functions: there is no regulated function that is continuous on ${\mathbb Q}\cap [0,1]$ and discontinuous on $[0,1]\setminus {\mathbb Q}$ .

4. (d) Generalised Volterra’s corollary (Theorem 1.5) for regulated functions and height countable D (or: countable D, or: strongly countable D).

5. (e) For a sequence $(X_{n})_{n\in {\mathbb N}}$ of finite sets in $[0,1]$ , the set $[0,1]\setminus \cup _{n\in {\mathbb N}}X_{n}$ is dense (or: not height countable, or: not countable, or: not strongly countable).

Proof First of all, Volterra’s theorem implies Volterra’s corollary (both restricted to regulated functions), as Thomae’s function T from (1.1) is readily defined using $\exists ^{2}$ , while the latter also shows that T is regulated and continuous exactly on ${\mathbb R}\setminus {\mathbb Q}$ .

Secondly, we now derive $\mathsf {NIN}_{\mathsf {alt}}$ from Volterra’s corollary as in item (c). To this end, let $(X_{n})_{n\in {\mathbb N}}$ be a sequence of finite sets such that $[0,1]=\cup _{n\in {\mathbb N}}X_{n}$ . Now use $\mu ^{2}$ to define the following function:

(3.1) $$ \begin{align} g(x):= \begin{cases} 0, & x\in {\mathbb Q},\\ \frac{1}{2^{n+1}}, & x \in {\mathbb R}\setminus {\mathbb Q} \wedge x\in X_{n} \text{ and } n \text{ is the least such number.} \end{cases} \end{align} $$

We have $0=g(0+)=g(0-)=g(x+)=g(x-)$ for any $x\in (0,1)$ , i.e., g is regulated. To establish this fact in our base theory, note that $\cup _{k\leq n}X_{k}$ is finite for any $n\in {\mathbb N}$ and can be enumerated, both thanks to $\mathsf {FIN}$ . As a result, g is continuous at any $x\in {\mathbb Q}\cap [0,1]$ and discontinuous at any $y\in [0,1]\setminus {\mathbb Q}$ . This contradicts Volterra’s corollary (for regulated functions), and $\mathsf {NIN}_{\mathsf {alt}}$ follows.

Thirdly, we derive Volterra’s corollary (for regulated functions) from $\mathsf {NIN}_{\mathsf {alt}}$ , by contraposition. To this end, let f be regulated, continuous on $[0,1]\cap {\mathbb Q}$ , and discontinuous on $[0,1]\setminus {\mathbb Q}$ . Now consider the following set

(3.2) $$ \begin{align}\textstyle X_{n}:=\big\{x\in (0,1): |f(x+)- f(x)|>\frac1{2^{n}} \vee |f(x-)- f(x)|>\frac1{2^{n}}\big\}, \end{align} $$

where we note that, e.g., the right limit $f(x+)$ for $x\in (0,1)$ equals $\lim _{k\rightarrow \infty }f(x+\frac {1}{2^{k}})$ ; the latter limit is arithmetical and hence $\mu ^{2}$ readily obtains it. Hence, the set $X_{n}$ from (3.2) can be defined in $\mathsf {ACA}_{0}^{\omega }$ . To show that $X_{n}$ is finite, suppose not and apply $\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ to find a sequence of reals in $X_{n}$ . By the Bolzano–Weierstrass theorem from [89, III.2], this sequence has a convergent sub-sequence, say with limit $c\in [0,1]$ ; then either $f(c-)$ or $f(c+)$ does not exist (using the usual epsilon-delta definition), a contradiction. Hence, $X_{n}$ is finite and by the assumptions on f, we have $D_{f}=\cup _{n\in {\mathbb N}}X_{n}= [0,1]\setminus {\mathbb Q}$ . Then $[0,1]=D_{f}\cup {\mathbb Q}=\big (\cup _{n\in {\mathbb N}}X_{n})\cup {\mathbb Q}$ shows that the unit interval is a union over ${\mathbb N}$ of finite sets, i.e., $\neg \mathsf {NIN}_{\mathsf {alt}}$ follows. One derives item (b) from $\mathsf {NIN}_{\mathsf {alt}}$ in the same way; indeed: $[0,1]=D_{f}\cup D_{g}$ in case item (b) is false for regulated $f, g:[0,1]\rightarrow {\mathbb R}$ , showing that the unit interval is the union over ${\mathbb N}$ of finite sets, yielding $\neg \mathsf {NIN}_{\mathsf {alt}}$ .

Fourth, we only need to show that $\mathsf {NIN}_{\mathsf {alt}}$ implies item (d), as ${\mathbb Q}$ is trivially (height) countable and dense. Hence, let f be regulated, continuous on $[0,1]\cap D$ , and discontinuous on $[0,1]\setminus D$ , where D is height countable and dense. In particular, assume $D=\cup _{n\in {\mathbb N}}D_{n}$ where $D_{n}$ is finite for $n\in {\mathbb N}$ . Now consider $X_{n}$ as in (3.2) from the above and note that $[0,1]\setminus D=\cup _{n\in {\mathbb N}}X_{n}$ . Hence, $[0,1]=\cup _{n\in {\mathbb N}}Y_{n}$ where $Y_{n}=X_{n}\cup D_{n}$ is finite (as the components are), i.e., $\neg \mathsf {NIN}_{\mathsf {alt}}$ follows.

Finally, we only need to show that $\mathsf {NIN}_{\mathsf {alt}}$ implies the final item (e). For the terms in brackets in the latter, this is trivial as (strongly) countable sets are height countable. For the density claim, let $(X_{n})_{n\in {\mathbb N}}$ be a sequence of finite sets and suppose $x_{0}\in [0,1]$ and $N_{0}\in {\mathbb N}$ are such that $B(x_{0}, \frac {1}{2^{N_{0}}})\cap \big ([0,1]\setminus \cup _{n\in {\mathbb N}}X_{n} \big )$ is empty. Hence, $B(x_{0}, \frac {1}{2^{N_{0}}})\subset \cup _{n\in {\mathbb N}}X_{n}$ and define the finite sets $Y_{n}:= X_{n}\cap B(x_{0}, \frac {1}{2^{N_{0}}})$ using $\exists ^{2}$ . This implies $B(x_{0}, \frac {1}{2^{N_{0}}})= \cup _{n\in {\mathbb N}}Y_{n}$ , which contradicts $\mathsf {NIN}_{\mathsf {alt}}$ , modulo the rescaling discussed in Remark 3.4.

The final item of the theorem essentially expresses the Baire category theorem restricted to the complement of finite sets, which are automatically open and dense.

3.3.2 Continuity and Riemann integration

We connect the uncountability of ${\mathbb R}$ to properties of regulated functions like continuity and Riemann integration.

First of all, we shall need the set of (dis)continuity points of regulated $f:[0,1]\rightarrow {\mathbb R}$ , definable via $\exists ^{2}$ as follows:

$$\begin{align*}C_{f}:=\{x\in (0,1): f(x)=f(x+)=f(x-)\} \text{ and } D_{f}=[0,1]\setminus C_{f}. \end{align*}$$

These sets occupy a central spot in the study of regulated functions. We have the following theorem, where most items exhibit some kind of robustness.

Theorem 3.7 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}+\mathsf {FIN}$ )

The following are equivalent.

1. (i) The uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}$ .

2. (ii) For any regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is $x\in [0,1]$ where f is continuous (or: quasi-continuous, or: lower semi-continuous).

3. (iii) Any regulated $f:[0,1]\rightarrow {\mathbb R}$ is pointwise discontinuous, i.e., the set $C_{f}$ is dense in the unit interval.

4. (iv) For regulated $f:[0,1]\rightarrow {\mathbb R}$ , the set $C_{f}$ is not height countable (or: not countable, or: not strongly countable, or: not enumerable).

5. (v) For regulated $f:[0,1]\rightarrow [0,1]$ such that the Riemann integral $\int _{0}^{1}f(x)dx$ exists and is $0$ , there is $x\in [0,1]$ with $f(x)=0$ Bourbaki ([10, p. 61]).

6. (vi) For regulated $f:[0,1]\rightarrow [0,1]$ such that the Riemann integral $\int _{0}^{1}f(x)dx$ exists and equals $0$ , the set $\{x \in [0,1]: f(x)=0\}$ is dense ([10, p. 61]).

7. (vii) Blumberg’s theorem [8] restricted to regulated functions on $[0,1]$ .

8. (viii) Measure theoretic Blumberg’s theorem [16]: for regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is a dense and uncountable (or: not strongly countable, or: not height countable) subset $D\subset [0,1]$ such that $f_{\upharpoonright D}$ is pointwise discontinuous.

9. (ix) For regulated $f:[0,1]\rightarrow (0, 1]$ , there exist $N\in {\mathbb N}, x\in [0,1]$ such that $(\forall y\in B(x, \frac {1}{2^{N}}))(f(y)\geq \frac {1}{2^{N}})$ .

10. (x) For regulated $f:[0,1]\rightarrow (0, 1]$ , there exist a dense set D such that $f_{\upharpoonright D}$ is locally bounded away from zero ⁹ (on D).

11. (xi) (FTC) For regulated $f:[0,1]\rightarrow {\mathbb R}$ such that $F(x):=\lambda x.\int _{0}^{x}f(t)dt$ exists, there is $x_{0}\in (0,1)$ where $F(x)$ is differentiable with derivative $f(x_{0})$ .

12. (xii) For any regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is a Darboux point.

13. (xiii) For any regulated $f:[0,1]\rightarrow {\mathbb R}$ , its Darboux points are dense.

14. (xiv) For any regulated $f:[0,1]\rightarrow {\mathbb R}$ with only removable discontinuities, there is $x\in [0,1]$ which is not a strict ¹⁰ local maximum.

Proof First of all, we prove item (ii) from $\mathsf {NIN}_{\mathsf {alt}}$ ; we may use Volterra’s corollary as in Theorem 3.6. Fix regulated $f:[0,1]\rightarrow {\mathbb R}$ and consider this case distinction:

• • If there is $q\in {\mathbb Q}\cap [0,1]$ with $f(q+)= f(q-)=f(q)$ , item (ii) follows.

• • If there is no such rational, then Volterra’s corollary guarantees there is $x\in [0,1]\setminus {\mathbb Q}$ such that f is continuous at x.

In each case, there is a point of continuity for f, i.e., item (ii) follows. To prove that item (ii) implies $\mathsf {NIN}_{\mathsf {alt}}$ , let $X:=\cup _{n\in {\mathbb N}}X_{n}$ be the union of finite sets $X_{n}\subset [0,1]$ and define h as in (2.2). As for g from (3.1) in Theorem 3.6, h is regulated. Item (ii) then provides a point of continuity $y\in [0,1]$ of h, which by definition must be such that $y\not \in X$ . The same holds for quasi- and lower semi-continuity.

The implication (iii) $\rightarrow $ (ii) is immediate (as the empty set is not dense in $[0,1]$ ). To prove (i) $\rightarrow $ (iii), let f be regulated and such that $C_{f}$ is not dense. To derive $\neg \mathsf {NIN}_{\mathsf {alt}}$ , consider $X_{n}$ as in (3.2), which is finite for all $n\in {\mathbb N}$ (as is proved using $\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ and the Bolzano–Weierstrass theorem). Since $C_{f}$ is not dense in $[0,1]$ , there is $y\in [0,1]$ and $N\in {\mathbb N}$ such that $B(y, \frac {1}{2^{N}})\cap C_{f}=\emptyset $ . By definition, the set $D_{f}=\cup _{n\in {\mathbb N}}X_{n}$ collects all points where f is discontinuous. Hence, $[0,1]\setminus C_{f}=D_{f}$ , yielding $B(y, \frac {1}{2^{N}})\subset D_{f}$ . Now define $Y_{n}=X_{n}\cap B(y, \frac {1}{2^{N}})$ , which is finite since $X_{n}$ is finite. Hence, $\cup _{n\in {\mathbb N}}Y_{n}=B(y, \frac {1}{2^{N}})$ , i.e., an interval can be expressed as the union over ${\mathbb N}$ of finite sets, which readily yields $\neg \mathsf {NIN}_{\mathsf {alt}}$ after rescaling as in Remark 3.4.

Regarding item (iv), it suffices to derive the latter from $\mathsf {NIN}_{\mathsf {alt}}$ , which is immediate as $D_{f}$ is height countable. Indeed, if $C_{f}$ is also height countable, then $[0,1]=C_{f}\cup D_{f}$ is height countable, contradicting $\mathsf {NIN}_{\mathsf {alt}}$ . In case $A\subset [0,1]$ is countable, then any $Y:[0,1]\rightarrow {\mathbb N}$ injective on A is also a height function, i.e., A is also height countable. The same holds for strongly countable and enumerable sets.

Regarding items (v) and (vi), the latter immediately follow from items (ii) and (iii). Indeed, in case $f(x)>0$ for $x\in C_{f}$ , then by continuity there are $k, N\in {\mathbb N}$ such that $f(y)>\frac {1}{2^{k}}$ for $y\in B(x, \frac {1}{2^{N+1}})$ , implying $\int _{0}^{1}f(x)dx>\frac {1}{2^{k}2^{N}}>0$ . Now assume item (v), let $(X_{n})_{n\in {\mathbb N}}$ be a sequence of finite sets, and let h be as in (2.2). The latter is Riemann integrable with $\int _{0}^{1}h(x)dx=0$ , which one shows via the usual ‘epsilon-delta’ definition and $\mathsf {FIN}$ . Any $y\in [0,1]$ such that $h(y)=0$ , also satisfies $y\not \in \cup _{n\in {\mathbb N}} X_{n}$ , i.e., $ \mathsf {NIN}_{\mathsf {alt}}$ follows.

Next, we clearly have (iii) $\rightarrow $ (vii) and (iv) $\rightarrow$ (viii) since $D=C_{f}$ is as required. To prove (vii) $\rightarrow \mathsf {NIN}_{\mathsf {alt}}$ , let $(X_{n})_{n\in {\mathbb N}}$ be a sequence of finite sets in $[0,1]$ and consider the regulated function h from (2.2). Let D be the dense set provided by item (vii) and consider $y\in D$ . In case $h(y)\ne 0$ , say $h(y)>\frac {1}{2^{k_{0}}}$ , use $\mathsf {FIN}$ to enumerate $\cup _{n\leq k_{0}+1} X_{n}$ . Hence, we can find $N\in {\mathbb N}$ such that for $z\in B(x, \frac {1}{2^{N}})$ , $h(z)<\frac {1}{2^{k_{0}+1}}$ , i.e., $h_{\upharpoonright D}$ is not continuous (on D). This contradiction implies that $h(y)=0$ , meaning $y\in [0,1]\setminus \cup _{n\in {\mathbb N}}X_{n}$ , i.e., $\mathsf {NIN}_{\mathsf {alt}}$ follows. A similar proof works for item (viii) by considering a point from the dense set of continuity points of $f_{\upharpoonright D}$ .

Next, (ii) (resp. (iii)) clearly implies (ix) (resp. (x)). To show that (ix) and (x) imply $\mathsf {NIN}_{\mathsf {alt}}$ , one proceeds as in the previous paragraphs. Similarly, (ii) (resp. (iii)) implies (xii) (resp. (xiii)), as any continuity point is a Darboux point, by definition. To show that (xii) implies $\mathsf {NIN}_{\mathsf {alt}}$ , one considers the function h as in (2.2) and notes that a Darboux point of h is not in $\cup _{n\in {\mathbb N}}X_{n}$ .

For item (xi), the usual epsilon-delta proof establishes that $F(x):=\int _{0}^{x}f(t)dt$ is continuous and that $F'(y)=f(y)$ in case f is continuous at y, i.e., item (ii) implies item (xi). As noted above, h as in (2.2) satisfies $H(x):=\int _{0}^{x}h(x)dt=0$ for any $x\in [0,1]$ , i.e., any $y\in (0,1)$ such that $H'(y)=0=h(y)$ is such that $y\not \in \cup _{n\in {\mathbb N}}X_{n}$ , yielding $\mathsf {NIN}_{\mathsf {alt}}$ as required.

Finally, assume item (xiv), let $(X_{n})_{n\in {\mathbb N}}$ be a sequence of finite sets, and note that h as in (2.2) is regulated with only removable discontinuities. Now, the set $X=\cup _{n\in {\mathbb N}}X_{n}$ consists of the local strict maxima of h, i.e., item (xiv) yields $\mathsf {NIN}_{\mathsf {alt}}$ . For the reversal, $\exists ^{2}$ computes a functional M such that $M(g, a, b)$ is a maximum of $g\in C([0,1])$ on $[a,b]\subset [0,1]$ (see [48, Section 3]), i.e., $(\forall y\in [a,b])(g(y)\leq g(M(g, a,b)))$ . Using the functional M, one readily shows that ‘x is a strict local maximum of g’ is decidable ¹¹ given $\exists ^{2}$ , for g continuous on $[0,1]$ . Now let $f:[0,1]\rightarrow {\mathbb R}$ be regulated and with only removable discontinuities. Use $\exists ^{2}$ to define $\tilde {f}:[0,1]\rightarrow {\mathbb R}$ as follows: $\tilde {f}(x):= f(x+)$ for $x\in [0, 1)$ and $\tilde {f}(1)=f(1-)$ . By definition, $\tilde {f}$ is continuous on $[0,1]$ , and $\exists ^{2}$ computes a (continuous) modulus of continuity, which follows in the same way as for Baire space (see, e.g., [47, Section 4]). In case f is discontinuous at $x\in [0,1]$ , the latter point is a strict local maximum of f if and only if $f(x)>f(x+)$ (or $f(x)>f(x-)$ in case $x=1$ ). Note that $\mu ^{2}$ (together with a modulus of continuity for $\tilde {f}$ ) readily yields $N_{f, x}\in {\mathbb N}$ such that $(\forall y\in B(x, \frac {1}{2^{N_{f,x}}}))( f(y)<f(x))$ , in case x is a strict local maximum of f. In case f is continuous at $x\in [0,1]$ , we can use $\exists ^{2}$ to decide whether x is a local strict maximum of $\tilde {f}$ . By Footnote 11, $\mu ^{2}$ again yields $N_{f, x}\in {\mathbb N}$ such that $(\forall y\in B(x, \frac {1}{2^{N}}))( \tilde {f}(y)<\tilde {f}(x)))$ , in case x is a strict local maximum of $\tilde {f}$ . Now consider the following set:

$$\begin{align*}\textstyle A_{n}:=\{x\in [0,1]: x \text{ is a strict local maximum of } \tilde{f} \text{ or } f \text{ with } n\geq N_{{f}, x} \}. \end{align*}$$

Then $A_{n}$ is finite as strict local maxima cannot be ‘too close’. Hence, $\mathsf {NIN}_{\mathsf {alt}}$ yields $y \in [0,1]\setminus \cup _{n\in {\mathbb N}}A_{n}$ , which is not a local maximum of f by definition, i.e., item (xiv) follows, and we are done.

We may view item (i) as an extremely basic version of the connectedness of $[0,1]$ , as defined by Jordan in [43, pp. 24–28]. Similarly, item (xi) is an extremely basic version of the fundamental theorem of calculus (FTC) and item (ii) is an extremely basic version of the Lebesgue criterion for Riemann integrability. Moreover, it seems necessary to formulate items (v), (vi), and (xi) with the extra condition that the functions at hand be Riemann integrable. As an exercise, the reader should prove that $h:[0,1]\rightarrow {\mathbb R}$ as in (2.2) is effectively Riemann integrable, i.e., there is a functional that outputs the ‘ $\delta>0$ ’ on input the ‘ $\varepsilon>0$ ’ as in the usual epsilon-delta definition of Riemann integrability.

Moreover, the notion of ‘left and right limits’ gives rise to the notion of ‘left and right derivatives’; following item (xi), the left (resp. right) limit of regulated $f:[0,1]\rightarrow {\mathbb R}$ equals the left (resp. right) derivative of F at every $x_{0}\in (0,1)$ via a completely elementary proof (say in $\mathsf {ACA}_{0}^{\omega }$ ). We could also formulate item (ii) with approximate continuity (see, e.g., [17, II.5]) in the conclusion, but this notion seems to involve a lot of measure theory.

3.3.3 Restrictions of regulated functions

In this section, we show that the above equivalences for $\mathsf {NIN}_{\mathsf {alt}}$ remain valid if we impose certain natural restrictions.

First of all, the above results show that we have to be careful with intuitive statements like regulated functions are ‘close to continuous’. Indeed, by Theorem 3.7, $\mathsf {Z}_{2}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ is consistent with the existence of regulated functions that are discontinuous everywhere. Similarly, $\mathsf {NIN}$ follows from the statement a regulated function is Baire 1 by [72, Theorem 2.34]. Hence, $\mathsf {Z}_{2}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ cannot prove the latter basic fact and the restriction in item (ii) in Theorem 3.8 is therefore non-trivial. Similar results hold for items items (iii)–(iv) in Theorem 3.8 following [72, Section 2.8].

Theorem 3.8 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}+\mathsf {FIN}$ )

The following are equivalent.

1. (i) The uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}$ .

2. (ii) For any regulated and Baire 2 function $f:[0,1]\rightarrow {\mathbb R}$ , there is $x\in [0,1]$ where f is continuous.

3. (iii) For any regulated and Baire 1 $^{*}$ function $f:[0,1]\rightarrow {\mathbb R}$ , there is $x\in [0,1]$ where f is continuous.

4. (iv) For any regulated and usco (or: lsco) function $f:[0,1]\rightarrow {\mathbb R}$ , there is $x\in [0,1]$ where f is continuous.

Proof In light of Theorem 3.7, we only need to show that items (ii)–(iv) imply $\mathsf {NIN}_{\mathsf {alt}}$ . The function $h:[0,1]\rightarrow {\mathbb R}$ from (2.2) is central in the proof of the former theorem. For item (ii), h is Baire 2 as follows: define $h_{n}(x)$ as $h(x)$ in case $x\in \cup _{m\leq n}X_{n}$ , and $0$ otherwise. By definition, h is the pointwise limit of $(h_{n})_{n\in {\mathbb N}}$ and $\mathsf {FIN}$ allows us to enumerate $\cup _{m\leq n_{0}}X_{n}$ for fixed $n_{0}\in {\mathbb N}$ . Hence, for fixed $n_{0}\in {\mathbb N}$ , $h_{n_{0}}$ has at most finitely many points of discontinuity. In particular, there is an obvious sequence of continuous function with pointwise limit $h_{n_{0}}$ , i.e., the latter is Baire 1. For item (iv), the function h is also usco as follows: in case $h(x_{0})=0$ for $x_{0}\in [0,1]$ , the definition of usco is trivially satisfied. In case $h(x_{0})=\frac {1}{2^{n+1}}$ , then there is $N\in {\mathbb N}$ such that $(\forall y\in B(x, \frac {1}{2^{N}}))( y\not \in \cup _{m\leq n-1}X_{m} )$ as in the proof of Theorem 3.7. In this case, the definition of usco is also satisfied. The function $\lambda x. (1-h(x))$ is lsco. For item (iii), define the closed sets $C_{n}:= \cup _{m\leq n}X_{m}$ and note that the restriction of h to $C_{n}$ is continuous for each n, i.e., h is also Baire 1 $^{*}$ .

Secondly, we point out one subtlety in the previous proof: it is only shown that $h:[0,1]\rightarrow {\mathbb R}$ from (2.2) is Baire 2. In particular, we cannot ¹² construct a double sequence of continuous functions with iterated limit equal to h. As it happens, Baire himself notes in [3, p. 69] that Baire 2 functions can be represented by such double sequences. We could generalise item (ii) in Theorem 3.8 to any higher Baire class and beyond, i.e., the latter theorem constitutes robustness in the flesh.

Moreover, going against our intuitions, we cannot replace ‘Baire 2’ by ‘Baire 1’ in Theorem 3.8 as the latter condition renders items (ii)–(iv) provable in $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ by the results in Section 3.5. In particular, while Baire $1^{*}$ and usco are subclasses of Baire 1, say in $\mathsf {ZF}$ or $\mathsf {Z}_{2}^{\Omega }$ , these inclusions do not necessarily hold in weaker systems. For instance, it is consistent with $\mathsf {Z}_{2}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ that there are totally discontinuous usco and regulated functions (see Theorem 3.7). An interesting RM-question would be to calibrate the strength of some of the well-known inclusions, like a regulated function on the unit interval is Baire 1.

Thirdly, the supremum principle for regulated functions implies $\mathsf {NIN}$ by [72, Theorem 2.32] where the former principle states the existence of $F:{\mathbb Q}^{2}\rightarrow {\mathbb R}$ such that $F(p, q)=\sup _{x\in [p,q]}f(x)$ for any $p, q\subset [0,1]\cap {\mathbb Q}$ . Indeed, using the well-known interval-halving technique, a supremum functional for $h:[0,1]\rightarrow {\mathbb N}$ as in (2.2) would allow us to enumerate the associated union $\cup _{n\in {\mathbb N}}X_{n}$ , i.e., $\mathsf {NIN}_{\mathsf {alt}}$ readily follows. Perhaps surprisingly, the equivalences for $\mathsf {NIN}_{\mathsf {alt}}$ from the previous sections still go through if we restrict to regulated functions with a supremum functional. Regarding item (iv), the Heaviside function is regulated but not symmetrically continuous, where the latter notion goes back to Hausdorff [32].

Theorem 3.9 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}+\mathsf {FIN}$ )

The following are equivalent.

1. (i) The uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}$ .

2. (ii) For regulated $f:[0,1]\rightarrow {\mathbb R}$ with a supremum functional, there is $x\in [0,1]$ where f is continuous.

3. (iii) For regulated and lsco $f:[0,1]\rightarrow {\mathbb R}$ with a supremum functional, there is $x\in [0,1]$ where f is continuous.

4. (iv) For regulated and symmetrically continuous $f:[0,1]\rightarrow {\mathbb R}$ , there is $x\in [0,1]$ where f is continuous.

Proof The first item implies the other items by Theorem 3.7. Now assume the second item and let $Y:[0,1]\rightarrow {\mathbb N}$ be an injection and define $e(x):= \sum _{n=0}^{Y(x)+1}\frac {x^{n}}{n!} $ . By definition, we have $e(x)<e^{x}$ for $x\in [0,1]$ . Using the second item of $\mathsf {FIN}$ , we have $e(x+)=e(x-)=e^{x}$ for $x\in (0,1)$ . Indeed, for small enough neighbourhoods U of $x\in (0,1)$ , Y is arbitrarily large on $U\setminus \{x\}$ , while $e^{x}$ is uniformly continuous on $[0,1]$ . Hence, $\lambda x.e(x)$ is regulated (and lsco) and $\sup _{x\in [p,q]}e(x)=e^{q}$ also follows. Since the former function is totally discontinuous, we obtain a contradiction. To show that $\lambda x.e(x)$ is also symmetrically continuous, note that the second item of $\mathsf {FIN}$ implies that $|e(x+h)-e(x-h)|$ is arbitrarily small for small enough $h\in {\mathbb R}$ .

Finally, there are a number of equivalent definitions of ‘Baire 1’ on the reals [4, 52, 57], including the following ones by [52, Theorem 2.3] and [55, Section 34, VII].

Definition 3.10.

• • Any $f:[0,1]\rightarrow {\mathbb R}$ is fragmented if for any $\varepsilon>0$ and closed $C\subset [0,1]$ , there is non-empty relatively ¹³ open $O\subset C$ such that $\mathsf {diam}(f(O))<\varepsilon $ .

• • Any $f:[0,1]\rightarrow {\mathbb R}$ is B-measurable of class 1 if for every open $Y\subset {\mathbb R}$ , the set $f^{-1}(Y)$ is $\textbf {F}_{\sigma }$ , i.e., a union over ${\mathbb N}$ of closed sets.

The diameter of a set X of reals is defined as usual, namely $\mathsf {diam}(X):=\sup _{x, y \in X}|x-y|$ , where the latter supremum need not exist for Definition 3.10. We have the following theorem, similar to Theorem 3.8.

Theorem 3.11 ( $\mathsf {ACA}_{0}^{\omega }+ \mathsf {IND}_{0}$ )

The following are equivalent.

1. (a) The uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}$ .

2. (b) For fragmented and regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is a point $x\in [0,1]$ where f is continuous.

3. (c) For B-measurable of class 1 and regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is $x\in [0,1]$ where f is continuous.

Proof In light of Theorem 3.7, it suffices to prove that h from (2.2) is fragmented and B-measurable of class $1$ . For the former notion, for fixed $k\in {\mathbb N}$ , $\mathsf {FIN}$ can enumerate the (finitely many) $x\in [0,1]$ such that $h(x)\geq \frac {1}{2^{k}}$ . Any open set O not including these points is such that $\textsf {diam}(h(O))<\frac {1}{2^{k}}$ , showing that h is fragmented.

For the B-measurability (of first class), in case $(X_{n})_{n\in {\mathbb N}}$ is a sequence of finite sets such that $[0,1]=\cup _{n\in {\mathbb N}}X_{n}$ , note that for any $Z\subset {\mathbb R}$ , the set $h^{-1}(Z)$ is the union of those $X_{n}$ such that $\frac {1}{2^{n+1}}\in Z$ , i.e., $\textbf {F}_{\sigma }$ by definition.

We show in Section 3.5 that most of the above statements that are equivalent to $\mathsf {NIN}_{\mathsf {alt}}$ , become provable in the much weaker system $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}+\mathsf {FIN}$ if we additionally require the functions to be Baire 1 as in Definition 1.8.

3.4 Bounded variation and the uncountability of ${\mathbb R}$

3.4.1 Introduction

In this section, we establish the equivalences sketched in Section 1.1 pertaining to the uncountability of ${\mathbb R}$ and properties of $BV$ -functions. In particular, we study the following weakening of $\mathsf {NIN}_{\mathsf {alt}}$ involving the notion of height-width countability from Definition 2.6.

Principle 3.12 ( $\mathsf {NIN}_{\mathsf {alt}}'$ )

The unit interval is not height–width countable.

Equivalences for $\mathsf {NIN}_{\mathsf {alt}}'$ will involve some (restrictions of) items from Theorems 3.6 and 3.7, but also a number of theorems from analysis that hold for $BV$ -functions and not for regulated ones. For the latter, we need some additional definitions, found in Section 3.4.2, while the equivalences are in Section 3.4.3

Finally, we first establish Theorem 3.15, which is interesting because we are unable to derive $\mathsf {NIN}_{\mathsf {alt}}$ from the items listed therein. The exact definitions of $\mathsf {HBU}$ and $\mathsf {WHBU}$ are below, where the former expresses that the uncountable covering $\cup _{x\in [0,1]}B(x, \Psi (x))$ has a finite sub-covering, i.e., the Heine-Borel theorem or Cousin lemma [21]. The principle $\mathsf {WHBU}$ is the combinatorial essence of the Vitali covering theorem, as studied in [66].

Principle 3.13 ( $\mathsf {HBU}$ [65])

For any $ \Psi :{\mathbb R}\rightarrow {\mathbb R}^{+}$ , there are $ y_{0}, \dots , y_{k}\in [0,1]$ such that $ \cup _{i\leq k}B(y_{i}, \Psi (y_{i}))$ covers $[0,1]$ .

Principle 3.14 ( $\mathsf {WHBU}$ [66])

For any $\Psi :{\mathbb R}\rightarrow {\mathbb R}^{+} $ and $ \varepsilon>_{{\mathbb R}}0$ , there are $ y_{0}, \dots , y_{k}\in [0,1]$ such that $\cup _{i\leq k}B(y_{i}, \Psi (y_{i}))$ has measure at least $1-\varepsilon $ .

We note that $\mathsf {WHBU}$ can be formulated without using the Lebesgue measure, as discussed at length in e.g., [66] or [89, X.1]. We conjecture that $\mathsf {NIN}_{\mathsf {alt}}$ is not provable in $\mathsf {ACA}_{0}^{\omega }+ \mathsf {HBU}$ .

Theorem 3.15 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {FIN}$ )

The following theorems imply $\mathsf {NIN}_{\mathsf {alt}}'$ :

• • Jordan decomposition theorem for $[0,1]$ ,

• • the principle $\mathsf {HBU}$ restricted to $BV$ -functions,

• • the principle $\mathsf {WHBU}$ restricted to $BV$ -functions.

Proof For the first item, let $(Y_{n})_{n\in {\mathbb N}}$ be a sequence of finite sets with width bound $g\in {\mathbb N}^{{\mathbb N}}$ . The function $k:[0,1]\rightarrow {\mathbb R}$ from (2.4) has bounded variation, with upper bound 1 by definition, for which we need $\mathsf {FIN}$ . By [70, Lemma 7], $\mu ^{2}$ can enumerate the points of discontinuity of a monotone function, i.e., the Jordan decomposition theorem provides a sequence $(x_{n})_{n\in {\mathbb N}}$ that enumerates the points of discontinuity of a $BV$ -function. Using the usual diagonal argument (see, e.g., [89, II.4.9]), we can find a point not in this sequence, yielding $\mathsf {NIN}_{\mathsf {alt}}'$ .

For the remaining items, let $(Y_{n})_{n\in {\mathbb N}}$ again be a sequence of finite sets with width bound $g\in {\mathbb N}^{{\mathbb N}}$ . Suppose $[0,1]=\cup _{n\in {\mathbb N}}Y_{n}$ and define $\Psi :[0,1]\rightarrow {\mathbb R}^{+}$ as follows $\Psi (x):= \frac {1}{2^{n+5}}\frac {1}{g(n)+1}$ where $x\in Y_{n}$ and n is the least such number. For $x_{0}, \dots , x_{k}\in [0,1]$ , the measure of $\cup _{i\leq k} B(x_{i}, \Psi (x_{i}))$ is at most $1/2$ by construction, contradicting $\mathsf {HBU}$ and $\mathsf {WHBU}$ . Using $\mathsf {FIN}$ , one readily shows that $\Psi $ is in $BV$ .

The principle $\mathsf {HBU}$ is studied in [5, 6] for $\Psi $ represented by, e.g., second-order Borel codes. This ‘coded’ version is provable in $\mathsf {ATR}_{0}$ extended with some induction. By contrast and Theorem 3.15, $\mathsf {HBU}$ restricted to $BV$ -functions, which are definitely Borel, implies $\mathsf {NIN}_{\mathsf {alt}}'$ , which in turn is not provable in $\mathsf {Z}_{2}^{\omega }$ . Thus, the use of codes fundamentally changes the logical strength of $\mathsf {HBU}$ . A similar argument can be made for the Jordan decomposition theorem, studied for second-order codes in [64].

3.4.2 Definitions

We introduce some extra definitions needed for the RM-study of $BV$ -functions as in Section 3.4.3.

First of all, we shall study unordered sums, which are a device for bestowing meaning upon ‘uncountable sums’ $\sum _{x\in I}f(x)$ for any index set I and $f:I\rightarrow {\mathbb R}$ . A central result is that if $\sum _{x\in I}f(x)$ somehow exists, it must be a ‘normal’ series of the form $\sum _{i\in {\mathbb N}}f(y_{i})$ , i.e., $f(x)=0$ for all but countably many $x\in [0,1]$ ; Tao mentions this theorem in [94, p. xii].

By way of motivation, there is considerable historical and conceptual interest in this topic: Kelley notes in [44, p. 64] that Moore’s study of unordered sums in [61] led to the concept of net with his student Smith [62]. Unordered sums can be found in (self-proclaimed) basic or applied textbooks [39, 90] and can be used to develop measure theory [44, p. 79]. Moreover, Tukey shows in [96] that topology can be developed using phalanxes, which are nets with the same index sets as unordered sums.

Now, unordered sums are just a special kind of net and $a:[0,1]\rightarrow {\mathbb R}$ is therefore written $(a_{x})_{x\in [0,1]} $ in this context to suggest the connection to nets. The associated notation $\sum _{x\in [0,1]}a_{x}$ is purely symbolic. We only need the following notions in the below. Let $\mathsf {fin}({\mathbb R})$ be the set of all finite sequences of reals without repetitions.

Definition 3.16. Let $a:[0,1]\rightarrow {\mathbb R}$ be any mapping, also denoted $(a_{x})_{x\in [0,1]}$ .

• • We say that $\sum _{x\in [0,1]} a_{x}$ is Cauchy if there is $\Phi :{\mathbb R}\rightarrow \mathsf {fin}({\mathbb R})$ such that for $\varepsilon>0$ and all $J\in \mathsf {fin}({{\mathbb R}})$ with $J\cap \Phi (\varepsilon )=\emptyset $ , we have $|\sum _{x\in J}a_{x}|<\varepsilon $ .

• • We say that $\sum _{x\in [0,1]}a_{x} $ is bounded if there is $N_{0}\in {\mathbb N}$ such that for any $J\in \mathsf {fin}({\mathbb R})$ , $N_{0}>|\sum _{x\in J}a_{x}|$ .

Note that in the first item, $\Phi $ is called a Cauchy modulus. For simplicity, we focus on positive unordered sums, i.e., $(a_{x})_{x\in [0,1]}$ such that $a_{x}\geq 0$ for $x\in [0,1]$ .

Secondly, there are many spaces between the regulated and $BV$ -functions, as discussed in Remark 3.23. We shall study one particular construct, called Waterman variation, defined as follows.

Definition 3.17. A decreasing sequence of positive reals $\Lambda =(\lambda _{n})_{n\in {\mathbb N}}$ is a Waterman sequence if $\lim _{n\rightarrow \infty }\lambda _{n}=0$ and $\sum _{n=0}^{\infty }\lambda _{n}=\infty $ .

Definition 3.18 (Waterman variation)

The function $f:[a,b]\rightarrow {\mathbb R}$ has bounded Waterman variation with sequence $\Lambda =(\lambda _{n})_{n\in {\mathbb N}}$ on $[a,b]$ if there is $k_{0}\in {\mathbb N}$ such that $k_{0}\geq \sum _{i=0}^{n} \lambda _{i} |f(x_{i})-f(x_{i+1})|$ for any finite collection of pairwise non-overlapping intervals $(x_{i}, x_{i+1})\subset [a,b]$ .

Note that Definition 3.18 is equivalent to the ‘official’ definition of Waterman variation by [1, Proposition 2.18]. In case $f:[0,1]\rightarrow {\mathbb R}$ has bounded Waterman variation (with sequence $\Lambda $ as in Definition 3.17), we write ‘ $f\in \Lambda BV$ ’.

Thirdly, we make use of the usual definitions of Fourier coefficients and series.

Definition 3.19. The Fourier series $S(f)(x)$ of $f:[-\pi , \pi ]\rightarrow {\mathbb R}$ at $x\in [-\pi , \pi ]$  is

(3.3) $$ \begin{align}\textstyle \frac{a_{0}}{2} + \sum_{n=1}^{\infty} ( a_{k} \cdot \cos(nx)+b_{k} \cdot \sin(nx) ), \end{align} $$

with Fourier coefficients $ a_{n} := \frac {1}{\pi }\int _{-\pi }^{\pi } f (t)\cos (nt)dt$ and $ b_{n} :=\frac 1\pi \int _{-\pi }^{\pi } f (t) \sin (nt)dt$ .

By the proof of Theorem 3.22, the Fourier coefficients and series of $k:[0,1]\rightarrow {\mathbb R}$ as in (2.2) all exist. Our study of the Fourier series $S(f)$ as in (3.3) will always assume (at least) that the Fourier coefficients of f exist. Functions of bounded variation are of course Riemann integrable and similarly have Fourier coefficients, but only in sufficiently strong systems that seem to dwarf $\mathsf {NIN}_{\mathsf {alt}}'$ .

3.4.3 Basic equivalences

We establish a number of equivalences for $\mathsf {NIN}_{\mathsf {alt}}'$ and basic properties of $BV$ -functions, some similar to those in Theorems 3.6 and 3.7, some new. We note that $\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ is no longer needed in the base theory.

Theorem 3.20 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {FIN}$ )

The following are equivalent.

1. (i) The uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}'$ .

2. (ii) For a positive unordered sum $\sum _{x\in [0,1]}a_{x}$ with upper bound (or Cauchy modulus; Definition 3.16), there is $y\in [0,1]$ such that $a_{y}=0$ .

3. (iii) For a positive unordered sum $\sum _{x\in [0,1]}a_{x}$ with upper bound (or Cauchy modulus; Definition 3.16), the set $\{ x\in [0,1]: a_{x}=0\}$ is dense (or: not height countable, or: not countable, or: not strongly countable).

4. (iv)-(xix) Any of items (b)–(d) from Theorem 3.6 or items (ii)–(xiv) from Theorem 3.7 restricted to $BV$ -functions.

5. (xx) For a Waterman sequence $\Lambda $ and $f:[0,1]\rightarrow {\mathbb R}$ in $\Lambda BV$ , there is $y\in [0,1]$ where f is continuous.

6. (xxi)-(xxxvi) Any of items (b)–(d) from Theorem 3.6 or items (ii)–(xiv) from Theorem 3.7 restricted to $\Lambda BV$ for any fixed Waterman sequence $\Lambda $ .

Proof The equivalences involving the restrictions from regulated to $BV$ functions follow from the proofs of Theorems 3.6 and 3.7. Indeed, for $f\in BV$ with variation bounded by $1$ , the set $X_{n}$ from (3.2) has size bounded by $2^{n}$ since each element of $X_{n}$ contributes at least $1/2^{n}$ to the variation. Moreover, rather than $h:[0,1]\rightarrow {\mathbb R}$ as in (2.2), we use $k:[0,1]\rightarrow {\mathbb R}$ as in (2.4) which has variation bounded by $1$ if $(Y_{n})_{n\in {\mathbb N}}$ is a sequence of sets with width function $g\in {\mathbb N}^{{\mathbb N}}$ . The properties of $k:[0,1]\rightarrow {\mathbb R}$ are readily proved using $\mathsf {FIN}$ ; in particular, the width function g obviates the use of $\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ as in the proofs of Theorems 3.6 and 3.7. Hence, the equivalence between $\mathsf {NIN}_{\mathsf {alt}}'$ and items (iv)–(xix) has been established.

The equivalence between items (i) and (ii) is as follows: assume the latter and let $(X_{n})_{n\in {\mathbb N}}$ and $g:{\mathbb N}\rightarrow {\mathbb N}$ be as in item (i). Define $(a_{x})_{x\in [0,1]}$ as follows:

$$\begin{align*}a_{x}:= \begin{cases} 0, & x\not \in \cup_{n\in {\mathbb N}} X_{n}, \\ \frac{1}{2^{n}}\frac{1}{g(n)+1}, & x\in X_{n} \text{ and } n \text{ is the least such natural.} \end{cases} \end{align*}$$

Clearly, this unordered sum is Cauchy and has upper bound $1$ ; if $y\in [0,1]$ is such that $a_{y}=0$ , then $y\not \in \cup _{n\in {\mathbb N}}X_{n}$ , as required for item (i). Now assume the latter and let $(a_{x})_{x\in [0,1]}$ be an unordered sum that is Cauchy. Now consider the following set:

(3.4) $$ \begin{align} X_{n}:=\{x\in [0,1]: a_{x}>1/2^{n}\}. \end{align} $$

Apply the Cauchy property of $(a_{x})_{x\in [0,1]}$ for $\varepsilon =1$ , yielding an upper bound $N_{0}\in {\mathbb N}$ for $\sum _{x\in K}a_{x}$ for any $K\in \mathsf {fin}{({\mathbb R})}$ . Hence, the finite set $X_{n}$ in (3.4) has size at most $2^{n}N_{0}$ . In this way, we have a width function for $(X_{n})_{n\in {\mathbb N}}$ ; any $y\in [0,1]\setminus \cup _{n\in {\mathbb N}}X_{n}$ is such that $a_{y}=0$ , as required for item (ii). Item (iii) now follows in the same way as for item (e) in the proof of Theorem 3.6.

For item (xx), assume the latter and note that (3.5) establishes that $f\in BV$ implies $f\in \Lambda BV$ for any Waterman sequence $\Lambda =(\lambda _{n})_{n\in {\mathbb N}}$ :

(3.5) $$ \begin{align}\textstyle \sum_{i=0}^{n} \lambda_{i} |f(x_{i})-f(x_{i+1})|\leq \sum_{i=0}^{n} \lambda_{1} |f(x_{i})-f(x_{i+1})|\leq \lambda_{1} V_{0}^{1}(f), \end{align} $$

as Waterman sequences are decreasing by definition. Hence, item (i) readily follows from item (xx). Now assume item (i) and recall that for $BV$ -functions with variation bounded by $1$ , the set $X_{n}$ from (3.2) can have at most $2^{n}$ elements, as each element of $X_{n}$ contributes at least $\frac {1}{2^{n}}$ to the total variation. Functions with Waterman variation bounded by $1$ similarly come with explicit upper bounds on the set $X_{n}$ , namely $|X_{n}|\leq K_{n}$ where $K_{n}$ is the least $k\in {\mathbb N}$ such that $2^{n}<\sum _{m=0}^{k}\lambda _{m}$ . Hence, item (xx) follows and we are done.

Following the proof of Theorem 3.8, we observe that we may restrict to $BV$ -function that are Baire 2 or Baire 1 $^{*}$ in the previous theorem. With the gift of hindsight we can even obtain the following corollary. We recall that the space of regulated functions is the union over all Waterman sequences $\Lambda =(\lambda _{n})_{n\in {\mathbb N}}$ of the spaces $\Lambda BV$ , as established in [1, Proposition 2.24].

Corollary 3.21 (Some generalisations)

• • We may replace ‘ $f\in \Lambda BV$ ’ in items (xx)–(xxxvi) of the theorem by ‘regulated function $f:[0,1]\rightarrow {\mathbb R}$ with $\Lambda =(\lambda _{n})_{n\in {\mathbb N}}$ such that $f\in \Lambda BV$ ’.

• • Assuming $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}+\mathsf {FIN}$ , the higher item implies the lower one.

  1. – For any regulated $f:[0,1]\rightarrow {\mathbb R}$ , there is a Waterman sequence $\Lambda =(\lambda _{n})_{n\in {\mathbb N}}$ such that $f\in \Lambda BV$ .

  2. – The uniform finite union theorem.

Proof For the first item, the last part of the proof of the theorem provides the required upper bound function for applying $\mathsf {NIN}_{\mathsf {alt}}'$ .

For the second item, let $(X_{n})_{n\in {\mathbb N}}$ be a sequence of finite sets in $[0,1]$ and consider the regulated function $h:[0,1]\rightarrow {\mathbb R}$ as in (2.2). Suppose h is in $\Lambda BV$ with $\Lambda =(\lambda _{n})_{n\in {\mathbb N}}$ and with upper bound $N_{0}\in {\mathbb N}$ on the Waterman variation. Then $A_{n+2}$ as in (2.1) is $\cup _{i\leq n}X_{i}$ for all $n\in {\mathbb N}$ and $|A_n| \leq K_{n}$ where $K_{n}$ is the least $k\in {\mathbb N}$ such that $2^{n}N_{0}<\sum _{m=0}^{k}\lambda _{m}$ . The uniform finite union theorem thus follows.

An equivalence is possible in the second item, but the technical details are considerable. Our above results suggest that the principles equivalent to $\mathsf {NIN}_{\mathsf {alt}}'$ also have a certain robustness since we can replace ‘one point’ properties like item (ii) in Theorem 3.20, by, e.g., ‘density’ versions like item (iii) in Theorem 3.20. Nonetheless, we believe we cannot replace ‘density’ by ‘full measure’. In particular, we conjecture that ‘measure theoretic’ statements like

• • a $BV$ -function is continuous (or differentiable) almost $^{14}$ everywhere,

• • a height–width countable set $A\subset [0,1]$ has measure ¹⁴ zero

are strictly stronger than $\mathsf {NIN}_{\mathsf {alt}}'$ . We do not have a proof of this claim.

Finally, the variation function $\lambda x. V_{a}^{x}(f)$ is defined in the obvious way, namely based on (1.2). This function shares pointwise properties like continuity and differentiability with $f:[a,b]\rightarrow {\mathbb R}$ . For instance, the following equivalence for any $x\in [0,1)$ is obtained in [37, Corollary 1.1]:

(3.6) $$ \begin{align} f \ \mathit{is \ right}\text{-}\mathit{continuous \ at} \ x \ \mathit{if \ and \ only \ if} \ \lambda x. V_{a}^{x}(f) \ \mathit{is \ right}\text{-}\mathit{continuous \ at} \ x. \end{align} $$

Here, ‘right-continuous at $y\in [0,1)$ ’ means $g(y)=g(y+)$ . Now, although the variation function may not exist for $BV$ -functions, say in $\mathsf {RCA}_{0}^{\omega }$ , the right-hand side of (3.6) makes sense using the well-known ‘virtual’ or ‘comparative’ meaning of suprema from second-order RM (see [89, X.1]). Perhaps surprisingly, working over $\mathsf {ACA}_{0}^{\omega }+\mathsf {FIN}+\neg \mathsf {NIN}_{\mathsf {alt}}'$ , the function $k:[0,1]\rightarrow {\mathbb R}$ from (2.4) satisfies

$$ \begin{align*} \mathit{the \ function} \ \lambda x.V_{0}^{x}(k) \ \mathit{is \ right}\text{-}\mathit{continuous \ for} \ x\in [0,1), \end{align*} $$

which is to be interpreted in the aforementioned virtual sense. Thus, one readily proves that the following are equivalent, where $E(f, x)$ is (3.6).

• • The uncountability of ${\mathbb R}$ as in $\mathsf {NIN}_{\mathsf {alt}}'$ .

• • For $f:[0,1]\rightarrow {\mathbb R}$ in $BV$ , there is $y\in [0,1]$ where f is continuous.

• • For $f:[0,1]\rightarrow {\mathbb R}$ in $BV$ , there is $y\in [0,1]$ where $E(f, y)$ holds.

• • For $f:[0,1]\rightarrow {\mathbb R}$ in $BV$ such that $\lambda x.V_{0}^{x}(f)$ is right-continuous on $[0,1)$ , there is $y\in [0,1]$ where f is right-continuous.

To be absolutely clear, we think this topic should not be pursued further: mistakes are (too) easily made when dealing with ‘virtual’ objects like $\lambda x.V_{0}^{x}(f)$ .

3.4.4 Advanced equivalences: Fourier series

We obtain an equivalence for $\mathsf {NIN}_{\mathsf {alt}}'$ and properties of the Fourier series of $BV$ -functions. Since the forward direction is rather involved, we have reserved a separate section for this result. Moreover, Theorem 3.22 is not at all straightforward: Jordan proves the convergence of Fourier series for $BV$ -functions using the Jordan decomposition theorem, and the same for, e.g., [106, pp. 57–58]. However, the latter theorem seems much stronger ¹⁵ than $\mathsf {NIN}_{\mathsf {alt}}'$ .

Theorem 3.22 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {FIN}$ )

The following are equivalent to $\mathsf {NIN}_{\mathsf {alt}}'$ .

• • For $f:[-\pi ,\pi ]\rightarrow {\mathbb R}$ in $BV$ such that the Fourier coefficients exist, there is $x_{0}\in (-\pi ,\pi )$ where the Fourier series $S(f)(x_{0})$ equals $f(x_{0})$ .

• • For $f:[-\pi ,\pi ]\rightarrow {\mathbb R}$ in $BV$ such that the Fourier coefficients exist, the set of $x\in (-\pi , \pi )$ where the Fourier series $S(f)(x)$ equals $f(x)$ , is dense (or: not height countable, or: not countable, or: not strongly countable).

Proof Assume the first item and consider $k:[0,1]\rightarrow {\mathbb R}$ from (2.4). This function is Riemann integrable with $\int _{0}^{1}k(x)dx=0$ , which one proves in the same way as for $h:[0,1]\rightarrow {\mathbb R}$ from (2.2) in the proof of Theorem 3.7. Similarly (and with a suitable rescaling), the Fourier coefficients of the Fourier series of k are zero. Hence, any $x_{0}$ where the Fourier series of k converges to $k(x_{0})$ must be such that $k(x_{0})=0$ , as required for $\mathsf {NIN}_{\mathsf {alt}}'$ since then $x_{0}\not \in \cup _{n\in {\mathbb N}}X_{n}$ .

Secondly, by items (iv)–(xix) in Theorem 3.20, $\mathsf {NIN}_{\mathsf {alt}}'$ implies that for a $BV$ -function, the set $C_{f}$ is dense (or: not height countable, or: not countable, or: not strongly countable). Hence, the second item from Theorem 3.22 is immediate if we can show that $S(f)(x)$ from Definition 3.19 equals $\frac {f(x+)-f(x-)}{2}$ for f in $BV$ and any x in the domain. Waterman provides an elementary and almost self-contained proof of this convergence fact in [101], avoiding the Jordan decomposition theorem and only citing [106, Vol. I, p. 55, (7.1)]. The proof of the latter is straightforward trigonometry and Waterman’s argument is readily formalised in $\mathsf {ACA}_{0}^{\omega }$ . Similarly, there are ‘textbook’ proofs that $S(f)(x)$ equals $\frac {f(x+)-f(x-)}{2}$ for f in $BV$ and x in the domain that avoid the Jordan decomposition theorem. Such proofs generally seem to proceed as follows (see, e.g., [51, 102, 106]).

• • By Fejér’s theorem ([106, p. 89] or [102, p. 170]), Fourier series of $BV$ -functions are convergent in the Césaro mean to $\frac {f(x+)-f(x-)}{2}$ .

• • For $BV$ -functions, Fourier coefficients are $O(\frac {1}{n})$ ([102, p. 172], [106, p. 48]).

• • By Hardy’s theorem ([106, p. 78] or [102, p. 156]), if a series converges in the Césaro mean, it also converges in case the terms are $O(\frac {1}{n})$ .

• • By Césaro’s method of summation (see [102, p. 155]), if a series converges in the Césaro mean to a limit s and the series also converges, then the series converges to the limit s.

Each of these results has an elementary (sometimes tedious and lengthy) proof that readily formalises in $\mathsf {ACA}_{0}^{\omega }$ . As an example, the proofs of the second item in [102, p. 172] and [1, p. 288] make use of the Jordan decomposition theorem, while the proofs in [92] and [106, p. 48] do not and are completely elementary. Finally, the perhaps ‘most elementary’ proof based on the above items is found in [51].

Regarding the conditional nature of the items in Theorem 3.22, the Fourier coefficients of $BV$ -functions of course exist by the Lebesgue criterion for the Riemann integral. However, that $BV$ -functions have a point of continuity is already non-trivial by items (iv)–(xix) in Theorem 3.20. Moreover, the Darboux formulation of the Riemann integral involves suprema of $BV$ -functions, which are hard to compute by the second cluster theorem in [71].

Finally, we could generalise the items from Theorems 3.20 and 3.22 to other notions of ‘generalised’ bounded variation. The latter notions yield (many) intermediate spaces between $BV$ and regulated as follows.

Remark 3.23 (Between bounded variation and regulated)

The following spaces are intermediate between $BV$ and regulated; all details may be found in [1].

Wiener spaces from mathematical physics [103] are based on p-variation, which amounts to replacing ‘ $ |f(x_{i})-f(x_{i+1})|$ ’ by ‘ $ |f(x_{i})-f(x_{i+1})|^{p}$ ’ in the definition of variation (1.2). Young [104] generalises this to $\phi $ -variation which instead involves $\phi ( |f(x_{i})-f(x_{i+1})|)$ for so-called Young functions $\phi $ , yielding the Wiener–Young spaces. Perhaps a simpler construct is the Waterman variation [100], which involves $ \lambda _{i}|f(x_{i})-f(x_{i+1})|$ and where $(\lambda _{n})_{n\in {\mathbb N}}$ is a sequence of reals with nice properties; in contrast to $BV$ , any continuous function is included in the Waterman space [1, Proposition 2.23]. Combining ideas from the above, the Schramm variation involves $\phi _{i}( |f(x_{i})-f(x_{i+1})|)$ for a sequence $(\phi _{n})_{n\in {\mathbb N}}$ of well-behaved ‘gauge’ functions [85]. As to generality, the union (resp. intersection) of all Schramm spaces yields the space of regulated (resp. $BV$ ) functions, while all other aforementioned spaces are Schramm spaces [1, Propositions 2.43 and 2.46]. In contrast to $BV$ and the Jordan decomposition theorem, these generalised notions of variation have no known ‘nice’ decomposition theorem. The notion of Korenblum variation [50] does have such a theorem (see [1, Proposition 2.68]) and involves a distortion function acting on the partition, not on the function values (see [1, Definition 2.60]).

It is no exaggeration to say that there are many natural spaces between the regulated and $BV$ -functions, all of which yield equivalences in Theorem 3.20.

3.5 When more is less in Reverse Mathematics

An important-if not central-aspect of analysis is the relationship between its many function classes. It goes without saying that these relationships need not hold in weak logical systems. For instance, the well-known inclusion regulated implies Baire 1 is not provable in $\mathsf {Z}_{2}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ by [72, Theorem 2.34].

In this section, we establish a kind of dual to the previous negative result: we show that most of the above statements that are equivalent to $\mathsf {NIN}_{\mathsf {alt}}$ or $\mathsf {NIN}_{\mathsf {alt}'}$ , become provable in the much weaker system $\mathsf {ACA}_{0}^{\omega }+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}+\mathsf {FIN}$ if we additionally require the functions to be Baire 1. To this end, we need the following theorem, where a jump continuity is any $x\in (0,1)$ such that $f(x+)\ne f(x-)$ .

Theorem 3.24 ( $\mathsf {ACA}_{0}^{\omega }$ )

If $f:[0,1]\rightarrow {\mathbb R}$ is regulated, there is a sequence of reals containing all jump discontinuities of f.

Proof This is immediate from [72, Theorem 2.16].

The following theorem should be contrasted with Theorems 3.8 and 3.20.

Theorem 3.25 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {FIN}$ )

For a Baire 1 function $f:[0,1]\rightarrow {\mathbb R}$ in $BV$ , the points of continuity of f are dense.

Proof Let $f:[0,1]\rightarrow {\mathbb R}$ be Baire $1$ and in $BV$ with variation bounded by $1$ . This function is regulated by Theorem 3.3. Use Theorem 3.24 to enumerate the jump discontinuities of f as $(y_{n})_{n\in {\mathbb N}}$ . Let $(f_{n})_{n\in {\mathbb N}}$ be a sequence of continuous functions with pointwise limit f on $[0,1]$ and consider the following formula:

(3.7) $$ \begin{align}\textstyle \varphi(n_{0}, k, x)\equiv(\forall n, m\geq n_{0})(\forall q\in B(x, \frac{1}{2^{m}})\cap {\mathbb Q})(|f_{n}(x)-f(q)|\geq \frac{1}{2^{k}}+\frac{1}{2^{n_{0}}}). \end{align} $$

For fixed $k\in {\mathbb N}$ , $\varphi (n_{0}, k, x)$ holds for large enough $n_{0}\in {\mathbb N}$ in case f has a removable discontinuity at $x\in (0,1)$ such that $|f(x)-f(x+)|>\frac 1{2^{k}}$ . For fixed $n_{0},k\in {\mathbb N}$ , there can only be $2^{k}$ many pairwise distinct $x\in [0,1]$ such that $\varphi (n_{0}, k, x)$ , as each such real contributes at least $\frac 1{2^{k}}$ to the total variation of f.

Next, the formula $\varphi (n_{0}, k, x)$ is equivalent to (second-order) $\Pi _{1}^{0}$ as f only occurs with rational input and $f_{n}$ can be replaced uniformly by a sequence of codes $\Phi _{n}$ . Moreover, in case $x=_{{\mathbb R}} y$ , then trivially $\varphi (n_{0}, k, x)\leftrightarrow \varphi (n_{0}, k, y)$ , i.e., we have the extensionality property required for [89, II.5.7]. By the latter there is an RM-code of a closed set $C_{n_{0},k}$ such that $x\in C_{n_{0},k}\leftrightarrow \varphi (n_{0}, k, x)$ for all $x\in {\mathbb R}$ and $n_{0}, k\in {\mathbb N}$ . Since $C_{n_{0}, k}$ is finite, $O_{n_{0}, k}:= [0,1]\setminus \big (C_{n_{0}, k}\cup \{y_{0}, \dots , y_{k}\} \big )$ is open and dense. By the Baire category theorem for RM-codes [89, II.5.8], the intersection $\cap _{n_{0}, k\in {\mathbb N}} O_{n_{0}, k} $ is dense in $[0,1]$ . By definition, this intersection does not contain any points of discontinuity of f, and we are done.

The following corollary should be contrasted with Theorem 3.22.

Corollary 3.26 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {FIN}$ )

• • For a positive unordered sum $\sum _{x\in [0,1]}a_{x}$ with upper bound and where $(a_{x})_{x\in [0,1]}$ is Baire 1, the set $\{y\in [0,1]:a_{y}=0\}$ is dense.

• • For Baire 1 function $f:[-\pi ,\pi ]\rightarrow {\mathbb R}$ in $BV$ such that the Fourier coefficients exist, the set $\{x\in (-\pi , \pi ): S(f)(x)=f(x)\}$ , is dense.

Proof Let $(a_{x})_{x\in [0,1]}$ be an unordered sum with upper bound $1$ . Now consider

(3.8) $$ \begin{align} X_{n}:=\{x\in [0,1]: a_{x}>1/2^{n}\}, \end{align} $$

which can have at most $2^{n}$ elements. As in the proof of the theorem, the Baire 1 approximation of $(a_{x})_{x\in [0,1]}$ allows us to show that $a_{x}>1/2^{n}$ is (implied by) a suitable (second-order) $\Sigma _{1}^{0}$ -formula. One then uses the (second-order) Baire category theorem to show that $y\in [0,1]$ such that $a_{y}=0$ are dense.

For the second item, following the proof of Theorem 3.22, $f(x)=S(f)(x)$ holds in case f is continuous at $x\in [0,1]$ , where the latter is provided by the theorem.

Next, the first item in Theorem 3.27 follows from [72, Theorem 2.26], but the latter is proved using $\mathsf {ACA}_{0}^{\omega }+\mathsf {ATR}_{0}$ .

Theorem 3.27 ( $\mathsf {ACA}_{0}^{\omega }+\mathsf {FIN}+\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ )

• • For regulated Baire 1 $f:[0,1]\rightarrow {\mathbb R}$ , the points of continuity of f are dense.

• • Volterra’s corollary: there is no regulated and Baire 1 function that is continuous on ${\mathbb Q}\cap [0,1]$ and discontinuous on $[0,1]\setminus {\mathbb Q}$ .

• • For a Riemann integrable and regulated $f:[0,1]\rightarrow [0,1]$ in Baire 1 with $\int _{0}^{1}f(x)dx=0$ , the set $\{x\in [0,1]:f(x)=0\}$ is dense.

• • Blumberg’s theorem [8] restricted to regulated Baire 1 functions on $[0,1]$ .

Proof For the first item, the proof of Theorem 3.25 can be modified follows: for regulated f and fixed $k\in {\mathbb N}$ , there can be at most finitely many $x\in [0,1]$ such that $|f(x)-f(x+)|>\frac 1{2^{k}}$ . One proves this fact by contradiction (as in the proof of Theorem 3.6), where $\mathsf {QF}\text{-}\mathsf {AC}^{0,1}$ provides a sequence $(x_{n})_{n\in {\mathbb N}}$ of reals in $ [0,1]$ such that $|f(x_{n})-f(x_{n}+)|>\frac 1{2^{k}}$ for all $n\in {\mathbb N}$ . This sequence has a convergent sub-sequence, say with limit $y\in [0,1]$ ; one readily verifies that $f(y+)$ or $f(y-)$ does not exist. The rest of the proof is now identical to that of Theorem 3.25.

For the second item, the proof of Theorem 3.25 is readily adapted as follows: let $(q_{n})_{n\in {\mathbb N}}$ be an enumeration of the rationals in $[0,1]$ and define $O_{n_{0}, k}'$ as $O_{n_{0},k}\setminus \{q_{0}, \dots , q_{k}\}$ . Then Theorem 3.25 must yield an irrational point of continuity, a contradiction.

For the third item, note that $f(x)=0$ must hold in case f is continuous at $x\in [0,1]$ , where the (dense set of the) latter is provided by the first item.

For the fourth item, this immediately follows from the first item.

We could obtain similar results for most items of Theorem 3.7 and related theorems. We could also replace ‘Baire 1’ by ‘effectively Baire 2’ in Theorem 3.8 where the latter means that the function is given as the pointwise iterated limit of a double sequence of continuous functions; however, this would require us to go up to at least $\mathsf {ATR}_{0}$ , as suggested by the results in [72, Section 2.6].