Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T09:11:22.675Z Has data issue: false hasContentIssue false
  • English
  • Français

A Boolean ultrapower which is not an ultrapower

Published online by Cambridge University Press:  12 March 2014

Bernd Koppelberg  and
Sabine Koppelberg
Bernd Koppelberg
Affiliation:
Seminar für Logik und Grundlagenforschung 53 Bonn, West Germany
Sabine Koppelberg
Affiliation:
Seminar für Logik und Grundlagenforschung 53 Bonn, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Several people have independently been studying Boolean ultrapowers recently; see for example [2], [3], [4], [6]. Boolean ultrapowers are a quite natural generalization of the well-known usual ultrapowers, but it seemed to be unknown whether every Boolean ultrapower is isomorphic to an ultrapower. We give a negative answer to that question. We further show that a Boolean ultrapower by an ℵ1-regular ultrafilter need not be ℵ2-universal, i.e. that Theorem 4.3.12 of [1] does not hold for Boolean ultrapowers.

Let B be a complete Boolean algebra (we identify the algebra with its underlying set), whose operations are denoted by +, ·, −, 0, 1, Σ, Π Let 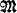be a structure for some language ℒ.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 1 , March 1976 , pp. 245 - 249
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[2] Foster, A. L., Generalized “Boolean” theory of universal algebras. I, Mathematische Zeitschrift, vol. 58 (1953), pp. 306–336.CrossRefGoogle Scholar
[3] Mansfield, R., The theory of Boolean ultrapowers, Annals of Mathematical Logic, vol. 2 (1971), pp. 297–323.CrossRefGoogle Scholar
[4] Potthoff, K., Boolean ultrapowers, Archiv für mathematische Logik, vol. 16 (1974), pp. 37–48.CrossRefGoogle Scholar
[5] Prikry, K., On descendingly complete ultrafilters (to appear).Google Scholar
[6] Ribenboim, P., Boolean powers, Fundamenta Mathematicae, vol. 65 (1969), pp. 243–268.CrossRefGoogle Scholar
[7] Sikorski, R., Boolean algebras, 2nd edition, Springer-Verlag, Berlin-Göttingen-Heidel-berg-New York, 1964.Google Scholar
[8] Solovay, R. M. and Tennenbaum, S., Iterated Cohen extensions and Souslin's problem, Annals of Mathematics, vol. 94 (1971).CrossRefGoogle Scholar