Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T11:28:26.575Z Has data issue: false hasContentIssue false
  • English
  • Français

A boundedness lemma for iterations

Published online by Cambridge University Press:  12 March 2014

Greg Hjorth
Greg Hjorth*
Affiliation:
Department of Mathematics, University of California, at Los Angeles, Los Angeles, CA 90095-1555, USA, E-mail: greg@math.ucla.edu URL: www.math.ucla.edu/~greg
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this paper is to present a kind of boundedness lemma for direct limits of coarse structural mice, and to indicate some applications to descriptive set theory. For instance, this allows us to show that under large cardinal or determinacy assumptions there is no prewellorder ≤ of length 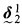such that for some formula ψ and parameter z

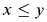
if and only if

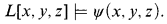
It is a peculiar experience to write up a result in this area. Following the work of Martin, Steel, Woodin, and other inner model theory experts, there is an enormous overhang of theorems and ideas, and it only takes one wandering pebble to restart the avalanche. For this reason I have chosen to center the exposition around the one pebble at 1.7 which I believe to be new. The applications discussed in section 2 involve routine modifications of known methods.

A detailed introduction to many of the techniques related to using the Martin-Steel inner model theory and Woodin's free extender algebra is given in the course of [1]. Certainly a familiarity with the Martin-Steel papers, [5] and [6], is a prerequisite, as is some knowledge of the free extender algebra. Probably anyone interested in this paper will already know the necessary descriptive set theory, most of which can be found in [4]. Discussion of earlier results in this direction can be found in [3] or [2].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 3 , September 2001 , pp. 1058 - 1072
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hjorth, G., Some applications of coarse inner model theory, this Journal, vol. 62 (1997), pp. 337–365.Google Scholar
[2]Hjorth, G., Two applications of inner model theory to sets, The Bulletin of Symbolic Logic, vol. 2 (1996), pp. 94–107.CrossRefGoogle Scholar
[3]Jackson, S., Partition properties and well-ordered sequences, Annals of Pure and Applied Logic, vol. 48 (1990), pp. 81–101.CrossRefGoogle Scholar
[4]Rechris, A. S., Martin, D. A., and Solovay, R. M., Introduction to Q-theory, Cabal seminar 79-81, Lecture Notes in Mathematics, vol. 1019, Springer, Berlin, 1983, pp. 199–282.CrossRefGoogle Scholar
[5]Martin, D. A. and Steel, J. R., A proof ofprojective determinacy, Journal of the American Mathematical Society, vol. 2 (1989), pp. 71–125.CrossRefGoogle Scholar
[6]Martin, D. A. and Steel, J. R., Iteration trees, Journal of the American Mathematical Society, vol. 7 (1994), pp. 1–73.CrossRefGoogle Scholar
[7]Neeman, I., Optimal proofs of determinacy, The Bulletin of Symbolic Logic, vol. 1 (1995), pp. 327–339.CrossRefGoogle Scholar
[8]Steel, J. R., HODL(ℝ) is a core model below θ, The Bulletin of Symbolic Logic, vol. 1 (1995), pp. 75–84.CrossRefGoogle Scholar