Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T18:43:53.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding prime models

Published online by Cambridge University Press:  12 March 2014

Barbara F. Csima ,
Denis R. Hirschfeldt ,
Julia F. Knight  and
Robert I. Soare
Barbara F. Csima
Affiliation:
Cornell University, Ithaca, New York 14853-4201, USA, E-mail: csima@math.cornell.edu
Denis R. Hirschfeldt
Affiliation:
University of Chicago, Chicago, Illinois 60637-1546, USA, E-mail: drh@math.uchicago.edu
Julia F. Knight
Affiliation:
Notre Dame University, South Bend, Indiana 46556, USA, E-mail: knight.l@nd.edu
Robert I. Soare
Affiliation:
University of Chicago, Chicago, Illinois 60637-1546, USA, E-mail: soare@math.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract.

A set X is prime bounding if for every complete atomic decidable (CAD) theory T there is a prime model 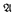of T decidable in X. It is easy to see that X = 0′ is prime bounding. Denisov claimed that every X <T 0′ is not prime bounding, but we discovered this to be incorrect. Here we give the correct characterization that the prime bounding sets X ≤τ 0′ are exactly the sets which are not low2. Recall that X is low2 if X″ ≤τ 0″. To prove that a low2 set X is not prime bounding we use a 0′ -computable listing of the array of sets {Y : Y ≤τX } to build a CAD theory T which diagonalizes against all potential X-decidable prime models 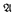of T, To prove that any non-low2X is indeed prime bounding. we fix a function f ≤TX that is not dominated by a certain 0′-computable function that picks out generators of principal types. Given a CAD theory T. we use f to eventually find, for every formula φ(x̄) con sistent with T. a principal type which contains it. and hence to build an X-decidable prime model of T. We prove the prime bounding property equivalent to several other combinatorial properties, including some related to the limitwise monotonic functions which have been introduced elsewhere in computable model theory.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 4 , December 2004 , pp. 1117 - 1142
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C. J. and Knight, J. F., Computable structures and the hyperarithmetical hierarchy, Elsevier Science, Amsterdam, 2000.Google Scholar
[2]Chang, C. C. and Keisler, H. J., Model theory, 3rd ed., Studies in Logic and the Foundations of Mathematics, vol. 73, North-Holland, Amsterdam, 1990, 1st ed. 1973, 2nd ed. 1977.Google Scholar
[3]Coles, R. J., Downey, R., and Khoussainov, B., On initial segments of computable linear orders, Order, vol. 14 (1998), pp. 107–124.Google Scholar
[4]Csima, B. F., Degree spectra of prime models, this Journal, vol. 69 (2004), pp. 430–442.Google Scholar
[5]Csima, B. F., Harizanov, V. S., Hirschfeldt, D. R., and Soare, R. I., Bounding homogeneous models, to appear.Google Scholar
[6]Denisov, A. S., Homogeneous 0′-elements in structural pre-orders, Algebra and Logic, vol. 28 (1989), pp. 405–418.CrossRefGoogle Scholar
[7]Drobotun, B. N.. Enumerations of simple models. Siberian Mathematics Journal, vol. 18 (1978), pp. 707–716.CrossRefGoogle Scholar
[8]Goncharov, S. S. and Nurtazin, A. T., Constructive models of complete decidable theories, Algebra and Logic, vol. 12 (1973), pp. 67–77.CrossRefGoogle Scholar
[9]Harizanov, V. S., Pure computable model theory, Handbook of recursive mathematics (Ershov, Yu. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, vol. 138–139, Elsevier Science, Amsterdam, 1998, pp. 3–114.Google Scholar
[10]Harizanov, V. S., Computability-theoretic complexity of countable structures, The Bulletin of Symbolic Logic, vol. 8 (2002), pp. 457–477.CrossRefGoogle Scholar
[11]Harrington, L., Recursively presentable prime models, this Journal, vol. 39 (1974), pp. 305–309.Google Scholar
[12]Hirschfeldt, D. R., Prime models of theories of computable linear orderings, Proceedings of the American Mathematical Society, vol. 129 (2001), pp. 3079–3083.CrossRefGoogle Scholar
[13]Jockusch, C. G. Jr., Degrees in which the recursive sets are uniformly recursive, Canadian Journal of Mathematics, vol. 24 (1972), pp. 1092–1099.CrossRefGoogle Scholar
[14]Jockusch, C. G. Jr. and Soare, R. I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[15]Kaplansky, I., Infinite Abelian groups, University of Michigan Press, 1954.Google Scholar
[16]Khisamiev, N. G., A constructibility criterion for the direct product of cyclic p-groups, Izvestiya Akademiya Nauk Kazakhstan SSR, Seriya Fiziko-Matematicheskaya, (1981), pp. 51–55, in Russian.Google Scholar
[17]Khisamiev, N. G., Theory of abelian groups with constructive models, Siberian Mathematics Journal, vol. 27 (1986), pp. 572–585.Google Scholar
[18]Khisamiev, N. G., Constructive abelian groups, Handbook of recursive mathematics (Ershov, Yu. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, vol. 138–139, Elsevier Science, Amsterdam, 1998, pp. 1177–1231.Google Scholar
[19]Khoussainov, B., Nies, A., and Shore, R. A., Computable models of theories with few models, Notre Dame Journal of Formal Logic, vol. 38 (1997), pp. 165–178.CrossRefGoogle Scholar
[20]Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
[21]Knight, J. F., Degrees of models, Handbook of recursive mathematics (Ershov, Yu. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, vol. 138–139, Elsevier Science, Amsterdam, 1998, pp. 289–309.Google Scholar
[22]Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für mathematische Logik unddie Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.Google Scholar
[23]Millar, T. S., Foundations of recursive model theory, Annals of Mathematical Logic, vol. 13 (1978), pp. 45–72.CrossRefGoogle Scholar
[24]Millar, T. S., Omitting types, type spectrums, and decidability, this Journal, vol. 48 (1983), pp. 171–181.Google Scholar
[25]Nies, A., A new spectrum of recursive models, Notre Dame Journal of Formal Logic, vol. 40 (1999), pp. 307–314.CrossRefGoogle Scholar
[26]Sacks, G. E., Saturated model theory, W. A. Benjamin, Inc., Reading, MA, 1972.Google Scholar
[27]Soare, R. I., Recursively enumerable sets and degrees: A study of computable functions and computably generated sets, Springer-Verlag, Heidelberg, 1987.CrossRefGoogle Scholar