Bounds for the closure ordinals of replete monotonic increasing functions

Extract

Whenever particular ordinals are used as tools in a proof or a definition, it is necessary to find a way of representing them. If the ordinals are sufficiently small, there is a standard way (e.g. Cantor normal forms for ordinals less than ε₀); in general, representations are often found by using functions on initial segments of the ordinals: Each term which can be obtained from 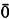by applications of a function symbol 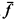is regarded as a notation for the ordinal obtained by the same applications of the function f to the ordinal 0. In this way, f provides representations for all the ordinals in Cl_f(0), the closure set of f (se e §1). (For an introduction to and development of this principle, see Feferman [F1]; and for a discussion of the significance of such representations in proof theory, see Kreisel [K1, pp. 22–34].) Thus it is natural to ask whether there are connections between frequently encountered properties of ordinal functions and the size of the ordinals for which they can provide representations.

The purpose of this paper is to show that, for any integer n, the ordinal 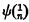(see §2) is a bound for the closure ordinals of replete monotonic increasing n-place functions. This result is optimal for n > 2 (the bound is attained by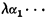 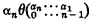where θα = 1 + α) but not for n < 2. D. H. de Jongh has recently proved, using a completely different method, that the (least possible) bound for n = 2 is ε₀. (Trivially, that for n = 1 is φ.)